경로계획(path planning)은 자율자동차, 로봇, 무인 항공기, 우주탐사 등과 같은 많은 분야에서 필수적인 요구사항이다. 경로계획법에는 여러 가지 방법이 제안되어 있는데, 최근 가장 인기를 모으는 방법으로는 RRT(rapidly exploring random tree)가 있다.
RRT는 샘플링 기반 경로계획법의 하나이다. 샘플링 기반 경로계획법은 형상공간을 격자(grid)로 분할하지 않고, 랜덤(random)하게 샘플점을 여러 개 생성하여 점점이(point-wise) 공간을 탐색하여 경로를 찾아내는 방법이다. 즉 형상공간(configuration space) 내에서 샘플점을 무작위로 충분한 수만큼 발생시키고 그 샘플점이, 혹은 두 개의 샘플점을 잇는 선이 장애물과 충돌하는 지 여부를 확인하여 자유공간(free space)의 구조를 효율적으로 파악한다.
랜덤 탐색은 특히 격자생성 방법으로는 탐색이 거의 불가능한 고차원(high dimension) 공간에서 강력한 힘을 발휘한다.
RRT는 LaValle에 의해 처음 제안되었는데, 기본 아이디어는 트리(tree)라고 불리는 특별한 그래프를 구축하는 것이다. 트리는 노드(vertex 또는 node)와 연결선(edge)로 구성된다. 연결선은 노드와 노드를 연결한 선이다.
트리 구조에서는 모든 노드는 부모(parent)라 불리는 1개의 다른 노드에 연결되며 시작점은 트리의 맨 상위 부모가 되는 루트(root)가 된다. RRT 알고리즘은 형상공간에서 시작점(initial point)과 목표점(goal point)을 연결한 트리를 산출한다.
RRT에서는 형상공간에서 랜덤하게 샘플점을 발생시킨 후 트리에서 가장 가까운 노드를 찾는다. 그리고 그 두 점을 직선으로 연결한 선상에 트리로부터 미리 설정한 거리만큼 떨어진 새로운 점을 트리로 편입한다. 만약 새로운 노드와 기존 노드를 연결한 직선, 즉 트리의 연결선(branch)이 장애물과 충돌한다면 새로운 샘플점을 랜덤하게 다시 발생시킨 후 같은 방법을 다시 시도한다. 이런 방법을 시작점에서 시작하여 목표점이 트리에 연결될 때 반복 시행하면서 트리를 확장시켜서 나가는데, 트리가 고차원의 형상공간속으로 신속하고 균일하게 확장되면서 자유공간을 효과적으로 탐색하게 된다.
RRT는 간단한 알고리즘이지만, 여러 가지 모양의 장애물이 있는 복잡한 환경 속에서도 효율적으로 경로를 생성시켜주기 때문에 로봇의 경로계획에 많이 사용되고 있다. 최근에는 RRT의 여러 가지 단점을 극복한 확장판 알고리즘이 많이 개발되면서 무인기의 경로계획에도 적용되기 시작하였다.
RRT 알고리즘을 구체적으로 살펴보자.
우선 트리를 초기화 한다. 초기화의 의미는 트리를 비운다는 뜻이다. 그리고 시작점을 트리에 편입한다. 시작점(\(\mathbf{q}_{ini}\))이 트리의 루트(root)가 되는 것이다. 시작점은 루트로서 부모 노드가 없기 때문에 공집합이다.
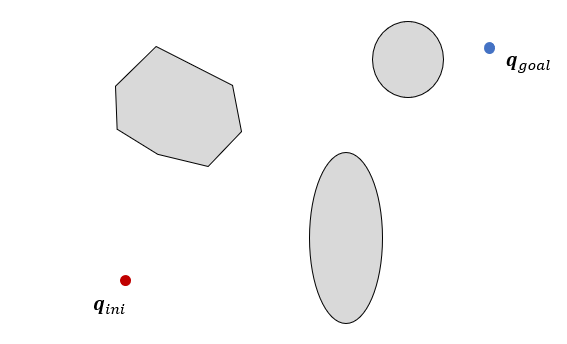
이제 트리를 목표점에 연결될 때까지 확장시킨다. 우선 샘플점(\(\mathbf{q}_{rand}\))을 한 개 발생시킨다. 그리고 트리에서 \(\mathbf{q}_{rand}\)와 가장 가까운 노드 \(\mathbf{q}_{near}\)를 찾는다.
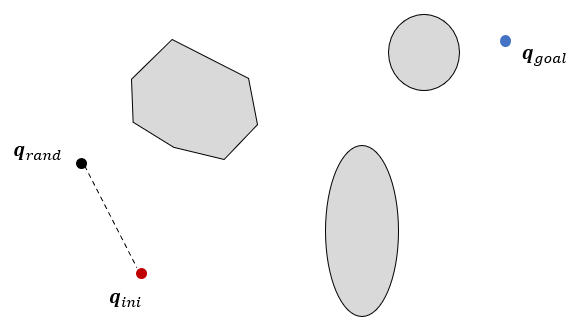
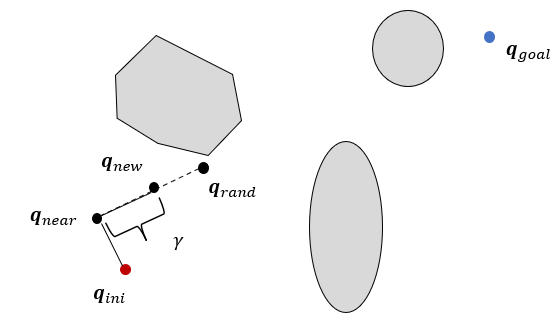
그 다음에는 노드 \(\mathbf{q}_{near}\)에서 \(\mathbf{q}_{rand}\)방향으로 연결한 직선상에 일정한 거리 \(\gamma\)만큼 떨어진 점을 새로운 노드 \(\mathbf{q}_{new}\)로 선정한다.

만약 \(\mathbf{q}_{near}\)에서 \(\mathbf{q}_{new}\)까지 직선으로 연결한 선이 장애물과 충돌하지 않으면 \(\mathbf{q}_{new}\)를 트리로 편입한다.
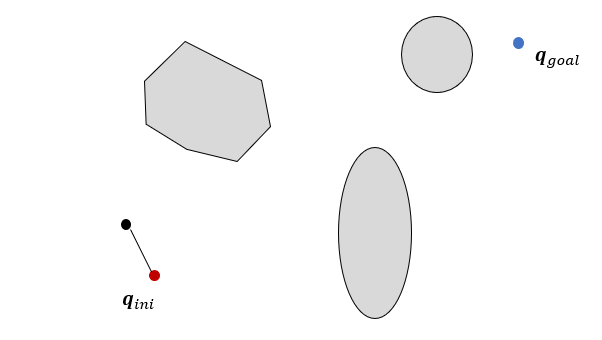
위 과정을 반복한다. 샘플점(\(\mathbf{q}_{rand}\))을 한 개 발생시킨다.

트리에서 \(\mathbf{q}_{rand}\)와 가장 가까운 노드 \(\mathbf{q}_{near}\)를 찾는다.
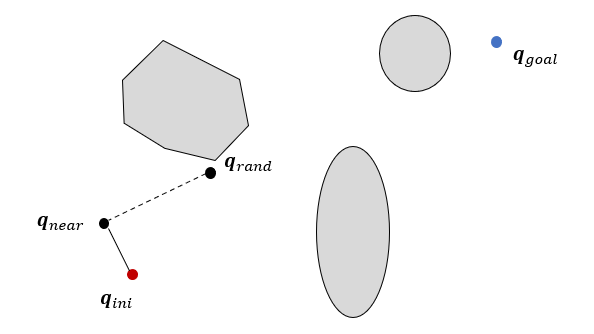
노드 \(\mathbf{q}_{near}\)에서 \(\mathbf{q}_{rand}\)방향으로 연결한 직선상에 일정한 거리 \(\gamma\)만큼 떨어진 점을 새로운 노드 \(\mathbf{q}_{new}\)로 선정한다.
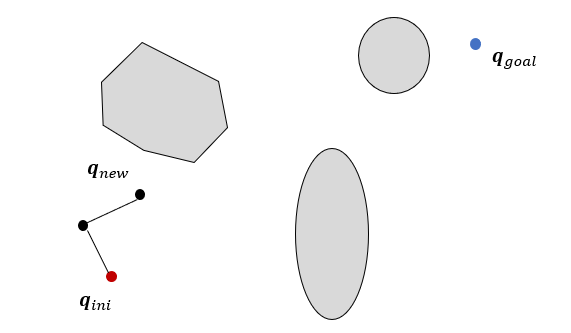
만약 \(\mathbf{q}_{near}\)에서\(\mathbf{q}_{new}\)까지 직선으로 연결한 선이 장애물과 충돌하지 않으면 \(\mathbf{q}_{new}\)를 트리로 편입한다.
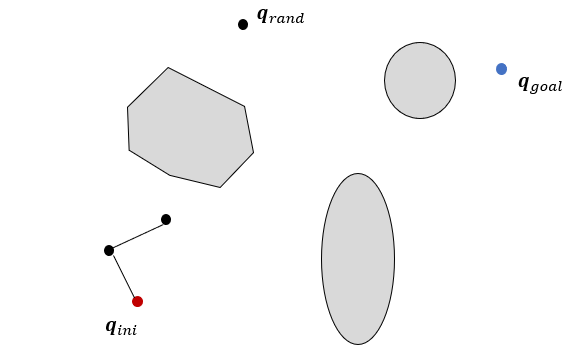
또다시 샘플점(\(\mathbf{q}_{rand}\))을 한 개 발생시킨다.
트리에서 \(\mathbf{q}_{rand}\)와 가장 가까운 노드 \(\mathbf{q}_{near}\)를 찾는다. 노드 \(\mathbf{q}_{near}\)에서 \(\mathbf{q}_{rand}\)방향으로 연결한 직선상에 일정한 거리 \(\gamma\)만큼 떨어진 점을 새로운 노드 \(\mathbf{q}_{new}\)로 선정한다.
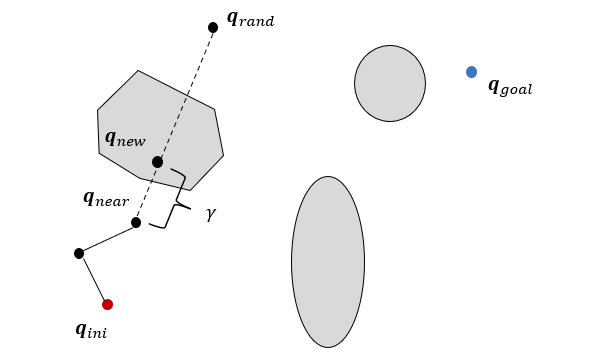
만약 장애물과 충돌한다면, \(\mathbf{q}_{rand}\)을 버리고, 샘플점 \(\mathbf{q}_{rand}\)을 다시 생성한다.
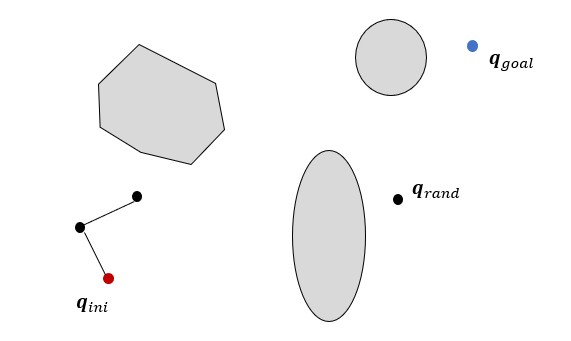
그리고 위 과정을 반복한다.
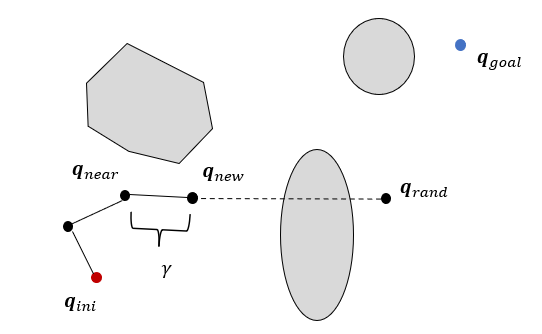
목표점이 트리의 노드와 연결되거나 혹은 매우 가까운 거리에 이르면 트리가 완성된 것으로 본다.
RRT는 여러 가지 모양의 장애물이 있는 환경에서도 효율적으로 경로를 생성시켜주고, 비선형 동적 프로그래밍이나 혼합-정수 선형 프로그래밍 또는 확률 로드맵보다도 계산량이 훨씬 적다는 장점에도 불구하고, 몇 가지 단점이 있다.
우선 샘플링 개수가 충분하지 않다면 존재하는 경로를 찾지 못할 수도 있다. 이것은 RRT만의 문제가 아니라 모든 샘플링 기반 경로계획법의 단점이라고 볼 수 있다. 또한 RRT 알고리즘으로 발생시킨 경로는 연결 가능(feasible)하지만 최적(optimal)이지 않다는 점이다. 실제로 RRT 알고리즘에서 경로를 생성할 때 어떠한 비용함수도 고려하지 않았다.
또한 RRT 알고리즘은 도착점까지 수렴하는데 많은 시간이 소요되며 예측 가능하지도 않다는 점이다. 그리고 산출된 경로가 랜덤 샘플링의 성격상 매우 삐뚤빼뚤하여 그대로는 구현 가능하지 않다는 문제도 있다.
그리고 로봇 또는 비행체의 운동학적 특성을 전혀 고려하지 않고 오로지 기하학적인 관계만을 이용했다는 점도 있다.
RRT의 단점을 해결하기 위하여 알고리즘을 개선하거나 확장시킨 다양한 RRT 변형버전이 많이 개발되었다.
'유도항법제어 > 유도항법' 카테고리의 다른 글
| 최적유도법칙 (Optimal Guidance Law): 최종 속도 미설정 (0) | 2023.09.17 |
|---|---|
| 최적 유도법칙 (Optimal Guidance Law): 최종 속도 설정 (0) | 2023.09.16 |
| 비례항법유도 (Proportional Navigation Guidance) (0) | 2023.03.11 |
| 포텐셜 필드 방법 (0) | 2021.01.29 |
| RRT* (RRT Star) 알고리즘 (0) | 2021.01.29 |




댓글