최적 유도법칙 (Optimal Guidance Law): 최종 속도 설정

중력장에서 비행체 또는 미사일의 운동 방정식은 다음과 같이 주어진다.

 

$$\begin{array}{r}\text{(1)}& \dot{\mathbf{r}}& =\mathbf{v}\\ \dot{\mathbf{v}}& =-\frac{\mu }{r^3}\mathbf{r}+\mathbf{a}\\ \\ & =\mathbf{g}(\mathbf{r})+\mathbf{a}\end{array}$$

 

여기서 $\mathbf{r}$ 과 $\mathbf{v}$ 는 각각 관성좌표계에 대한 위치벡터와 속도벡터를 나타낸다. $\mathbf{a}$ 는 제어 가속도, $\mu$ 는 중력파라미터, $\mathbf{g}(\mathbf{r})$ 은 비행체 또는 미사일에 작용하는 중력 가속도로서 위치의 함수이다.

 

 

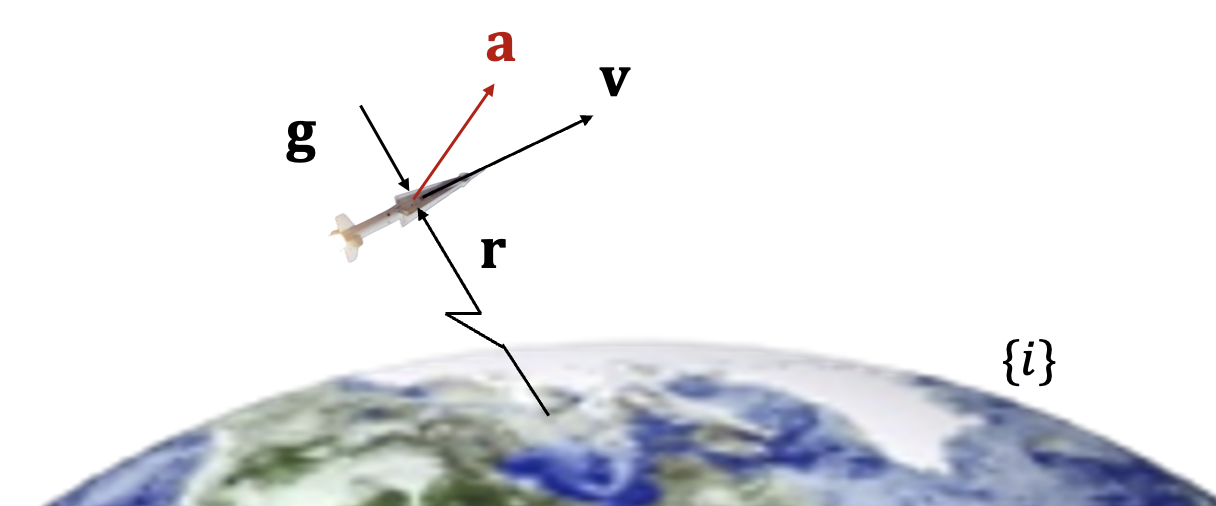
제어의 목적은 시간 $t_0$ 에서 출발지를 출발하여 최소의 에너지를 사용하여 시간 $t_f$ 에 목적지에 비행체를 도착시키는 것이다. 이 제어 목적을 실현시키기 위하여 최소화해야 할 비용함수와 제약조건은 다음과 같다.

 

$$\begin{array}{r}\text{(2)}& & J=\frac{1}{2}{\int }_{t_0}^{t_f}{\mathbf{a}}^T\mathbf{a}dt\\ \text{(3)}& & \mathbf{r}(t_0)={\mathbf{r}}_0,\mathbf{r}(t_f)={\mathbf{r}}_f\\ & \mathbf{v}(t_0)={\mathbf{v}}_0,\mathbf{v}(t_f)={\mathbf{v}}_f\end{array}$$

 

식 (1)~(3)으로 주어지는 최적제어 문제는 위성이나 적 비행체의 요격, 달 또는 지구로의 정밀 착륙, 지상 목표물의 타격 임무 등에 적용될 수 있는 유도법칙 설계 문제이기도 하다.

 

 

식 (1)에서 중력 가속도는 일반적으로 위치의 함수이지만 여기서는 해석적인 해를 유도하기 위하여 상수벡터로 가정하겠다. 즉, $\mathbf{g}(\mathbf{r})=\mathbf{g}$. 이 경우 식 (1), (3)은 다음과 같이 상태변수 방정식으로 표현할 수 있다.

 

$$\begin{array}{}\text{(4)}& \dot{\mathbf{x}}=A\mathbf{x}+B(\mathbf{a}+\mathbf{g})\end{array}$$

여기서

$$\begin{array}{rl}& A=\left[\begin{array}{cc}0& I\\ 0& 0\end{array}\right],B=\left[\begin{array}{c}0\\ I\end{array}\right]\\ \\ & \mathbf{x}=\left[\begin{array}{c}\mathbf{r}\\ \mathbf{v}\end{array}\right],\mathbf{x}(t_0)=\left[\begin{array}{c}{\mathbf{r}}_0\\ {\mathbf{v}}_0\end{array}\right],\mathbf{x}(t_f)=\left[\begin{array}{c}{\mathbf{r}}_f\\ {\mathbf{v}}_f\end{array}\right]\end{array}$$

 

이다. 식 (2)와 (4)로 주어지는 최적제어 문제는 예제(https://pasus.tistory.com/258, https://pasus.tistory.com/259)에서 풀었던 최종상태가 설정된 LQR 문제와 거의 동일하지만, 여기서 다시 자세히 풀어보도록 한다.

먼저 해밀토니안(Hamiltonian) 함수를 정의한다.

 

$$\begin{array}{}\text{(5)}& \mathcal{H}=\frac{1}{2}({\mathbf{a}}^T\mathbf{a})+{\lambda }^T(A\mathbf{x}+B(\mathbf{a}+\mathbf{g}))\end{array}$$

 

그러면 다음과 같이 상태변수와 코스테이트(costate) 미분 방정식을 얻을 수 있다.

 

$$\begin{array}{r}\text{(6)}& \dot{\mathbf{x}}& =\frac{\partial \mathcal{H}}{\partial \lambda }=A\mathbf{x}+B(\mathbf{a}+\mathbf{g})\\ -\dot{\lambda }& =\frac{\partial \mathcal{H}}{\partial \mathbf{x}}=A^T\lambda \end{array}$$

 

코스테이트 미분 방정식은 상태변수와 독립이므로 다음과 같이 쉽게 해를 구할 수 있다.

 

$$\begin{array}{}\text{(7)}& \lambda (t)=e^{A^T(t_f-t)}\lambda (t_f)\end{array}$$

 

정정조건(stationary condition)은 다음과 같다.

 

$$\begin{array}{}\text{(8)}& 0=\frac{\partial \mathcal{H}}{\partial \mathbf{a}}=B^T\lambda +\mathbf{a}\end{array}$$

 

따라서 최적제어는 식 (8)과 (7)로부터 다음과 같이 계산할 수 있다.

 

$$\begin{array}{r}\text{(9)}& \mathbf{a}(t)& =-B^T\lambda (t)\\ & =-B^T{e}^{A^T(t_f-t)}\lambda (t_f)\end{array}$$

 

식 (9)를 식 (4)에 대입하면 상태변수 미분 방정식은 다음과 같이 된다.

 

$$\begin{array}{}\text{(10)}& \dot{\mathbf{x}}=A\mathbf{x}+B(\mathbf{g}-B^T{e}^{A^T(t_f-t)}\lambda (t_f))\end{array}$$

 

위 식을 풀면 $\mathbf{x}(t)$ 를 다음과 같이 계산할 수 있다.

 

$$\begin{array}{r}\text{(11)}& \mathbf{x}(t)& =e^{A(t-t_0)}\mathbf{x}(t_0)+{\int }_{t_0}^t{e}^{A(t-\tau )}d\tau B\mathbf{g}\\ & -{\int }_{t_0}^t{e}^{A(t-\tau )}B{B}^T{e}^{A^T(t_f-\tau )}d\tau \lambda (t_f)\end{array}$$

 

위 식에 의하면 $t=t_f$ 에서 $\mathbf{x}(t_f)$ 를 다음과 같이 구할 수 있다.

 

$$\begin{array}{r}\text{(12)}& \mathbf{x}(t_f)& =e^{A(t_f-t_0)}\mathbf{x}(t_0)+{\int }_{t_0}^{t_f}{e}^{A(t_f-\tau )}d\tau B\mathbf{g}\\ & -{\int }_{t_0}^{t_f}{e}^{A(t_f-\tau )}B{B}^T{e}^{A^T(t_f-\tau )}d\tau \lambda (t_f)\end{array}$$

 

이 값이 $\mathbf{x}(t_f)={\mathbf{x}}_f$ 가 되도록 $\lambda (t_f)$ 를 계산해야 한다. 여기서 $G(t)$ 를 다음과 같이 정의하면,

 

$$\begin{array}{}\text{(13)}& G(t)={\int }_t^{t_f}{e}^{A(t_f-\tau )}B{B}^T{e}^{A^T(t_f-\tau )}d\tau \end{array}$$

 

$\lambda (t_f)$ 를 다음과 같이 계산할 수 있다.

 

$$\begin{array}{}\text{(14)}& \lambda (t_f)=-G^{-1}(t_0)({\mathbf{x}}_f-{\int }_{t_0}^{t_f}{e}^{A(t_f-\tau )}d\tau B\mathbf{g}-e^{A(t_f-t_0)}\mathbf{x}(t_0))\end{array}$$

 

마지막으로 식 (14)를 식 (9)에 대입하면 최적제어는

 

$$\begin{array}{}\text{(15)}& \mathbf{a}(t)=B^T{e}^{A^T(t_f-t)}{G}^{-1}(t_0)({\mathbf{x}}_f-{\int }_{t_0}^{t_f}{e}^{A(t_f-\tau )}d\tau B\mathbf{g}-e^{A(t_f-t_0)}\mathbf{x}(t_0))\end{array}$$

 

이 된다. 이 최적제어는 현재의 상태변수와 무관하고 상태변수의 초기값 $\mathbf{x}(t_0)$ 와 최종값 ${\mathbf{x}}_f$ 에만 영향을 받으므로 오픈루프(open-loop) 제어이다. 따라서 만약 어떤 이유로 시스템이 교란(perturbed)된다면 최종값에 도달하지 못할 수도 있다. 따라서 최적제어가 초기 상태변수 $\mathbf{x}(t_0)$ 대신에 현재의 상태변수 $\mathbf{x}(t)$ 의 함수가 되도록 식을 조금 변형해 보자.

 

 

식 (12)는 시간 $t_0$ 에서 상태변수 $\mathbf{x}(t_0)$ 가 주어졌을 때 $\mathbf{x}(t_f)$ 를 계산하는 식이다. 이 식은 임의의 시간 $t_0\le t_f$ 에서 상태변수 $\mathbf{x}(t_0)$ 가 주어졌을 때에도 모두 성립하는 식이기 때문에, 시간 $t\le t_f$ 에서 상태변수 $\mathbf{x}(t)$ 가 주어졌을 때에도 성립해야 한다.

 

$$\begin{array}{r}\text{(16)}& \mathbf{x}(t_f)& =e^{A(t_f-t)}\mathbf{x}(t)+{\int }_t^{t_f}{e}^{A(t_f-\tau )}d\tau B\mathbf{g}\\ & -{\int }_t^{t_f}{e}^{A(t_f-\tau )}B{B}^T{e}^{A^T(t_f-\tau )}d\tau \lambda (t_f)\end{array}$$

 

따라서 식 (14)는 다음과 같이 수정된다.

 

$$\begin{array}{}\text{(17)}& \lambda (t_f)=-G^{-1}(t)({\mathbf{x}}_f-{\int }_t^{t_f}{e}^{A(t_f-\tau )}d\tau B\mathbf{g}-e^{A(t_f-t)}\mathbf{x}(t))\end{array}$$

 

최적제어도 식 (18)과 같이 수정되므로 최적제어는 이제 최종 상태변수와 함께 현재의 상태변수 $\mathbf{x}(t)$ 의 피드백 제어가 된다.

 

$$\begin{array}{}\text{(18)}& \mathbf{a}(t)=B^T{e}^{A^T(t_f-t)}{G}^{-1}(t)({\mathbf{x}}_f-{\int }_t^{t_f}{e}^{A(t_f-\tau )}d\tau B\mathbf{g}-e^{A(t_f-t)}\mathbf{x}(t))\end{array}$$

 

이제 식 (18)을 구성하는 행렬을 차례로 계산해 보자. 먼저 행렬지수함수는 다음과 같이 계산된다.

 

$$\begin{array}{}\text{(19)}& e^{A(t_f-t)}=I+A(t_f-t)=\left[\begin{array}{cc}I& (t_f-t)I\\ 0& I\end{array}\right]\end{array}$$

 

행렬 $G(t)$ 는 정의와 식 (19)에 의해서 다음과 같이 계산된다.

 

$$\begin{array}{r}\text{(20)}& G(t)& ={\int }_t^{t_f}{e}^{A(t_f-\tau )}B{B}^T{e}^{A^T(t_f-\tau )}d\tau \\ & ={\int }_t^{t_f}\left[\begin{array}{cc}I& (t_f-\tau )I\\ 0& I\end{array}\right]\left[\begin{array}{c}0\\ I\end{array}\right]\left[\begin{array}{cc}0& I\end{array}\right]\left[\begin{array}{cc}I& 0\\ (t_f-\tau )I& I\end{array}\right]d\tau \\ \\ & ={\int }_t^{t_f}\left[\begin{array}{cc}(t_f-\tau {)}^{2}I& (t_f-\tau )I\\ (t_f-\tau )I& I\end{array}\right]d\tau \\ \\ & ={\left[\begin{array}{cc}-\frac{(t_f-\tau {)}^3}{3}I& -\frac{(t_f-\tau {)}^2}{2}I\\ -\frac{(t_f-\tau {)}^2}{2}I& \tau I\end{array}\right]}_t^{t_f}\\ \\ & =\left[\begin{array}{cc}\frac{t_{go}^3}{3}I& \frac{t_{go}^2}{2}I\\ \frac{t_{go}^2}{2}I& t_{go}I\end{array}\right]\end{array}$$

 

여기서 $t_{go}=t_f-t$ 는 잔여시간(time-to-go)을 나타낸다. $G(t)$ 의 역행렬은 다음과 같다.

 

$$\begin{array}{r}\text{(21)}& G^{-1}(t)& =\frac{12}{t_{go}^4}\left[\begin{array}{cc}{t}_{go}I& -\frac{t_{go}^2}{2}I\\ -\frac{t_{go}^2}{2}I& \frac{t_{go}^3}{3}I\end{array}\right]\\ & =\left[\begin{array}{cc}\frac{12}{t_{go}^3}I& -\frac{6}{t_{go}^2}I\\ -\frac{6}{t_{go}^2}I& \frac{4}{t_{go}}I\end{array}\right]\end{array}$$

 

식 (19)와 (21)을 이용하면 식 (18)의 구성 부분을 다음과 같이 계산할 수 있다.

 

$$\begin{array}{r}\text{(22)}& & B^T{e}^{A^T(t_f-t)}{G}^{-1}(t)=\left[\begin{array}{cc}\frac{6}{t_{go}^2}I& -\frac{2}{t_{go}}I\end{array}\right]\\ \text{(23)}& & {\int }_t^{t_f}{e}^{A(t_f-\tau )}d\tau B\mathbf{g}=\left[\begin{array}{c}\frac{t_{go}^2}{2}\mathbf{g}\\ t_{go}\mathbf{g}\end{array}\right]\\ \text{(24)}& & {\mathbf{x}}_f-{\int }_t^{t_f}{e}^{A(t_f-\tau )}d\tau B\mathbf{g}-e^{A(t_f-t)}\mathbf{x}(t)\\ & =\left[\begin{array}{c}{\mathbf{r}}_f-\frac{t_{go}^2}{2}\mathbf{g}-\mathbf{r}(t)-t_{go}\mathbf{v}(t)\\ {\mathbf{v}}_f-t_{go}\mathbf{g}-\mathbf{v}(t)\end{array}\right]\end{array}$$

 

식 (22), (23), (24)를 식 (18)에 대입하면 최적제어는 다음과 같다.

 

$$\begin{array}{rl}\text{(25)}& \mathbf{a}(t)& =\frac{6}{t_{go}^2}{\mathbf{r}}_f-3\mathbf{g}-\frac{6}{t_{go}^2}\mathbf{r}(t)-\frac{6}{t_{go}}\mathbf{v}(t)& -\frac{2}{t_{go}}{\mathbf{v}}_f+2\mathbf{g}+\frac{2}{t_{go}}\mathbf{v}(t)\\ \\ & =\frac{6}{t_{go}^2}({\mathbf{r}}_f-(\mathbf{r}(t)+t_{go}\mathbf{v}(t)+\frac{1}{2}{t}_{to}^2\mathbf{g}))\\ & -\frac{2}{t_{go}}({\mathbf{v}}_f-(\mathbf{v}(t)+t_{go}\mathbf{g}))\\ \\ & =\frac{6}{t_{go}^2}ZEM-\frac{2}{t_{go}}ZEV\end{array}$$

 

여기서 ZEM(Zero-Effort-Miss) 거리와 ZEV(Zero-Effort-Velocity)는 다음과 같이 정의된다.

 

$$\begin{array}{rl}\text{(26)}& & ZEM={\mathbf{r}}_f-(\mathbf{r}(t)+t_{go}\mathbf{v}(t)+\frac{1}{2}{t}_{to}^2\mathbf{g})& ZEV={\mathbf{v}}_f-(\mathbf{v}(t)+t_{go}\mathbf{g})\end{array}$$

 

정의에 의하면 ZEM과 ZEV는 현재 시간 $t$ 에서 임무 종료 시간 $t_f$ 까지 제어 가속도가 $0$ 일 때, 즉 zero-effort 일 때 임무 종료 시에 예측되는 거리와 속도 오차를 뜻한다.

식 (25)를 최종 속도가 설정된 경우의 최적 피드백 유도법칙(optimal feedback guidance law)이라고 한다. 최적 피드백 유도법칙은 최종 시간이 설정되어 있으므로 미리 결정된 시간에 요격을 달성하는 데 필요한 가속도 명령을 계산한다.

최종 속도벡터 ${\mathbf{v}}_f$ 에 대해서는 랑데부나 요격 등의 임무 조건에 따라 벡터의 방향과 크기가 요구조건으로 제시될 수 있다.

 

 

대부분의 종말 유도 단계에서는 중력 가속도를 상수라고 가정할 수 있지만 중력 가속도를 위치의 함수로 모델링해야 하는 경우도 있을 수 있다. 예를 들면 임무 비행시간 동안 비행체 또는 미사일의 운동에 상당한 고도 변화를 수반하는 경우를 들 수 있겠다. 이러한 경우에 제어 가속도가 중력 가속도를 직접적으로 보상할 수 있다는 가정하에 식 (25)의 최적 유도법칙을 수정할 수 있다. 즉, 식 (1)의 제어 가속도를 다음과 같이 분할한다면,

 

$$\begin{array}{}\text{(27)}& \mathbf{a}={\mathbf{a}}_1-\mathbf{g}(\mathbf{r})\end{array}$$

 

동일한 유도 방법을 통하여 식 (25)를 다음과 같이 수정할 수 있다.

 

$$\begin{array}{}\text{(28)}& \mathbf{a}(t)=\frac{6}{t_{go}^2}({\mathbf{r}}_f-(\mathbf{r}(t)+t_{go}\mathbf{v}(t)))-\frac{2}{t_{go}}({\mathbf{v}}_f-\mathbf{v}(t))-\mathbf{g}(\mathbf{r})\end{array}$$

 

식 (1)의 운동 방정식은 또한 일정한 속도로 비행하는 목표물과의 상대 운동 방정식과 형태가 동일하므로 식 (25)와 (27)의 유도법칙은 고정된 목적지 뿐만 아니라 일정한 속도로 비행하는 목표물을 요격하는 데도 사용할 수 있다. 그림은 미사일과 적 항공기간의 기하학적인 관계를 보여준다. $\{i\}$ 는 관성좌표계를 나타내며, ${\mathbf{r}}_m,{\mathbf{r}}_T$ 는 각각 미사일과 적 항공기의 위치벡터이고, ${\mathbf{v}}_m,{\mathbf{v}}_T$ 는 각각 미사일과 적 항공기의 속도벡터이다. ${\mathbf{a}}_m$ 은 미사일의 가속도 명령(command)이다. $\mathbf{r}={\mathbf{r}}_T-{\mathbf{r}}_m,\mathbf{v}={\mathbf{v}}_T-{\mathbf{v}}_m$ 은 각각 미사일과 적 항공기간의 상대 거리벡터와 상대 속도벡터이다.

 

 

그러면 다음과 같은 운동 방정식이 성립한다.

 

$$\begin{array}{r}\text{(29)}& & \dot{\mathbf{r}}=\mathbf{v}\\ & \dot{\mathbf{v}}=-\mathbf{g}-{\mathbf{a}}_m\end{array}$$

 

식 (29)와 (1)의 차이는 가속도 벡터의 부호가 서로 반대라는 것 밖에 없다.