비례항법유도 (Proportional Navigation Guidance)

1940년대에 경험적 유도법칙(guidance law)으로 시작된 이래 비례항법유도(PNG, proportional navigation guidance) 법칙은 현재 운용 중인 많은 전술 유도 미사일의 중기(midcourse) 및 종말단계(terminal phase)에서 가장 널리 사용되는 유도법칙일 뿐만 아니라 랑데부와 같은 우주임무의 유도 법칙으로도 사용되고 있다.

 

 

이와 같이 비례항법유도 법칙이 아직까지 각광을 받는 이유는 표적(target)에 관해 필요한 정보량이 적어서 온보드 센서요구 사항이 단순하므로 구현이 상대적으로 쉽고 신뢰성과 견고성이 뛰어나기 때문이다.

PNG가 경험적 유도법칙으로 시작하였다지만 여기서는 논문 "Fundamentals of proportional navigation by S. Murtaugh and H. Criel" 을 참고하여 유도법칙을 '유도'해 보겠다. 먼저 다음 그림과 같이 미사일과 표적의 기하학적인 관계가 있다고 하자.

 

 

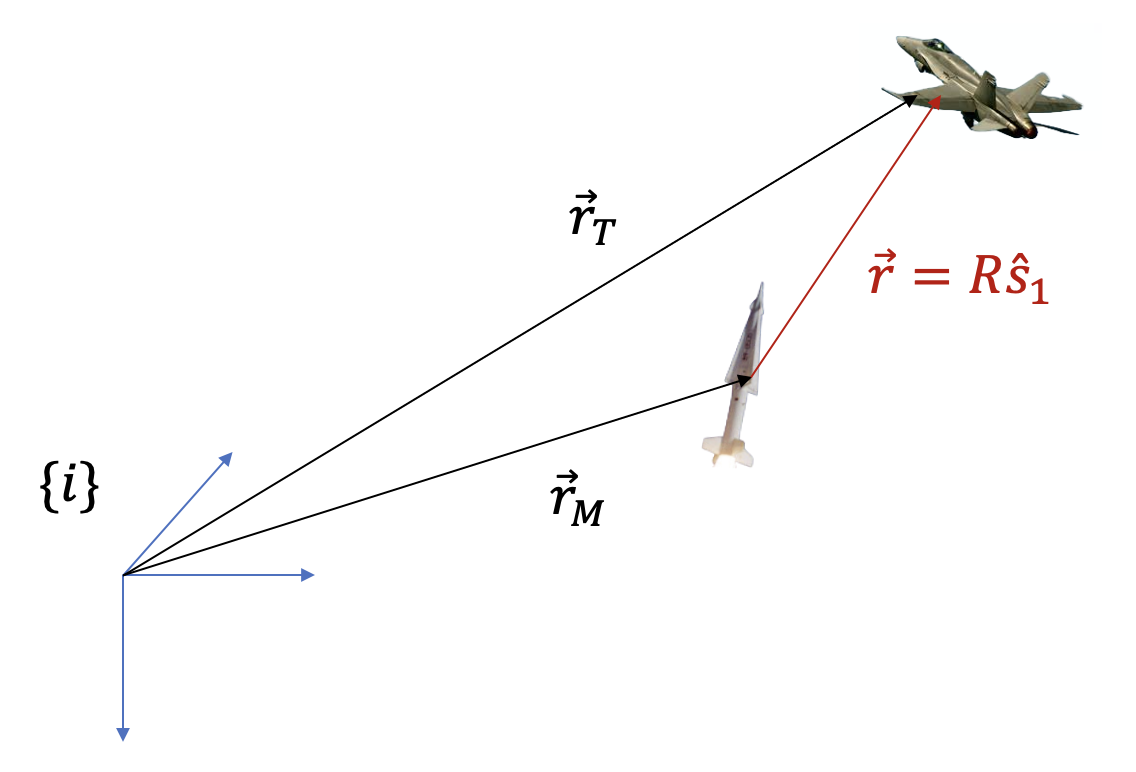
그림에서 $\{i\}$ 는 관성좌표계이고 ${\overrightarrow{r}}_T$ 는 관성좌표계의 원점에서 표적까지의 위치벡터, ${\overrightarrow{r}}_M$ 은 관성좌표계의 원점에서 미사일까지의 위치벡터, $\overrightarrow{r}$ 은 미사일에서 표적까지의 상대 위치벡터이다.

 

$$\begin{array}{r}\text{(1)}& \overrightarrow{r}& ={\overrightarrow{r}}_T-{\overrightarrow{r}}_M\\ & =R{\hat{s}}_1\end{array}$$

 

여기서 $R$ 은 미사일에서 표적까지의 거리이고, ${\hat{s}}_1$ 은 미사일과 표적을 잇는 가시선(LOS, line-of-sight)의 단위벡터다. 이제 상대 위치벡터 $\overrightarrow{r}$ 을 관성좌표계에서 미분하여 상대 속도벡터 $\overrightarrow{v}$ 를 구해보자.

 

$$\begin{array}{r}\text{(2)}& \overrightarrow{v}& =\frac{{}^{i}d\overrightarrow{r}}{dt}={\overrightarrow{v}}_T-{\overrightarrow{v}}_M\\ & =\frac{{}^{s}d\overrightarrow{r}}{dt}{+}^i{\overrightarrow{\omega }}^s\times \overrightarrow{r}\\ \\ & =\dot{R}{\hat{s}}_1+R{}^i{\overrightarrow{\omega }}^s\times {\hat{s}}_1\end{array}$$

 

여기서 $\{s\}$ 는 LOS 단위벡터를 ${\hat{s}}_1$ 축으로 하는 LOS 좌표계이다. LOS좌표계의 ${\hat{s}}_2$ 와 ${\hat{s}}_3$ 축은 상황에 맞게 적절히 선정할 수 있으나, 여기서는 유도법칙의 '유도' 과정을 쉽게 하기 위해서 다음과 같이 정하도록 하겠다.

 

$$\begin{array}{r}\text{(3)}& & {\hat{s}}_2=\frac{{}^i{\overrightarrow{\omega }}^s\times {\hat{s}}_1}{{\Vert }^i{\overrightarrow{\omega }}^s\times {\hat{s}}_1\Vert }\\ & {\hat{s}}_3={\hat{s}}_1\times {\hat{s}}_2\end{array}$$

 

즉, ${\hat{s}}_2$ 축은 LOS 벡터와 좌표계 $\{s\}$ 의 각속도 벡터 ${}^i{\overrightarrow{\omega }}^s$ 와 서로 수직인 방향으로 정하며 ${\hat{s}}_3$ 축은 오른손 법칙에 의해서 정한다.

상대 속도벡터 $\overrightarrow{v}$ 를 한번 더 미분하면 상대 가속도 벡터를 구할 수 있다.

 

$$\begin{array}{r}\text{(4)}& \overrightarrow{a}& =\frac{{}^{i}d\overrightarrow{v}}{dt}={\overrightarrow{a}}_T-{\overrightarrow{a}}_M\\ & =\ddot{R}{\hat{s}}_1{+}^i{\overrightarrow{\omega }}^s\times \dot{R}{\hat{s}}_1+\frac{{}^{s}d{}^i{\overrightarrow{\omega }}^s}{dt}\times \overrightarrow{r}+{}^i{\overrightarrow{\omega }}^s\times (\dot{R}{\hat{s}}_1+R{}^i{\overrightarrow{\omega }}^s\times {\hat{s}}_1)\\ \\ & =\ddot{R}{\hat{s}}_1+2\dot{R}{}^i{\overrightarrow{\omega }}^s\times {\hat{s}}_1+R\frac{{}^{s}d{}^i{\overrightarrow{\omega }}^s}{dt}\times {\hat{s}}_1+R{}^i{\overrightarrow{\omega }}^s\times ({}^i{\overrightarrow{\omega }}^s\times {\hat{s}}_1)\end{array}$$

 

여기서 ${}^i{\overrightarrow{\omega }}^s$ 가 좌표계 $\{s\}$ 로 ${}^i{\overrightarrow{\omega }}^s={\omega }_1{\hat{s}}_1+{\omega }_2{\hat{s}}_2+{\omega }_3{\hat{s}}_3$ 와 같이 표현된다면 식 (4)에서,

 

$$\begin{array}{}\text{(5)}& {}^i{\overrightarrow{\omega }}^s\times {\hat{s}}_1={\omega }_3{\hat{s}}_2-{\omega }_2{\hat{s}}_3\end{array}$$

 

가 되고, 식 (5)와 (3)을 비교하면 ${\omega }_2=0$ 이라는 것을 알 수 있다. 따라서 식 (5)는 다음과 같이 된다.

 

$$\begin{array}{}\text{(6)}& {}^i{\overrightarrow{\omega }}^s\times {\hat{s}}_1={\omega }_3{\hat{s}}_2\end{array}$$

 

식 (6)을 (4)에 대입하면 상대 가속도 벡터는 다음과 같이 된다.

 

$$\begin{array}{r}\text{(7)}& \overrightarrow{a}& ={\overrightarrow{a}}_T-{\overrightarrow{a}}_M\\ & =\ddot{R}{\hat{s}}_1+2\dot{R}{\omega }_3{\hat{s}}_2+R{\dot{\omega }}_3{\hat{s}}_2+R({\omega }_1{\hat{s}}_1+{\omega }_3{\hat{s}}_3)\times ({\omega }_3{\hat{s}}_2)\\ \\ & =(\ddot{R}-R{\omega }_3^2){\hat{s}}_1+(2\dot{R}{\omega }_3+R{\dot{\omega }}_3){\hat{s}}_2+R{\omega }_1{\omega }_3{\hat{s}}_3\end{array}$$

 

식 (7)에 의하면 미사일이 표적을 요격하기 위한, 즉 $R\to 0$ 이 되기 위한 충분조건은 ${\omega }_3=0$, $\ddot{R}\le 0$, $\dot{R}(0)<0$ 이다. 이 조건이 충족되면 표적과의 거리 $R$ 이 시간에 따라 단조 감소한다. 따라서 다음과 같이 접근속력(closing speed)을 정의하면

 

$$\begin{array}{}\text{(8)}& V_c=-\dot{R}\end{array}$$

 

$V_c>0$ 이 된다. 이제 이 충분조건을 충족시킬 수 있는 미사일 가속도를 구해 보도록 한다.

만약 표적의 가속도가 ${\overrightarrow{a}}_T=0$ 이라면 식 (7)에서 다음 식이 성립한다.

 

$$\begin{array}{r}\text{(9)}& -{\overrightarrow{a}}_M\cdot {\hat{s}}_2& =2\dot{R}{\omega }_3+R{\dot{\omega }}_3\\ & =-2V_c{\omega }_3+R{\dot{\omega }}_3\end{array}$$

 

식 (9)에서 미사일 가속도를 다음과 같이 정하면,

 

$$\begin{array}{}\text{(10)}& {\hat{a}}_M\cdot {\hat{s}}_2=N{V}_c{\omega }_3\end{array}$$

 

식 (9)는 다음과 같이 된다.

 

$$\begin{array}{}\text{(11)}& {\dot{\omega }}_3=-\frac{(N-2)V_c}{R}{\omega }_3\end{array}$$

 

여기서 $N$ 을 항법상수라고 한다. 식 (11)에 의하면 미사일 가속도가 식 (10)으로 주어질 때 $N>2$ 이면 ${\omega }_3\to 0$ 이 된다.

 

 

관성좌표계에 대한 좌표계 $\{s\}$ 의 각속도 벡터 ${}^i{\overrightarrow{\omega }}^s$ 는 LOS 단위벡터의 회전속력 ${\omega }_1$ 까지 포함하고 있으므로 다음과 같이 분리하도록 한다.

 

$$\begin{array}{}\text{(12)}& {}^i{\overrightarrow{\omega }}^s={\omega }_1{\hat{s}}_1+\overrightarrow{\mathrm{\Omega }}\end{array}$$

 

여기서 $\overrightarrow{\mathrm{\Omega }}$ 는 순수하게 LOS 단위벡터 ${\hat{s}}_1$ 의 각속도 만을 표현한 것이므로 LOS 각속도(angular velocity) 벡터라고 한다. 미사일의 시커(seeker)가 측정하거나 추정할 수 있는 물리량은 ${}^i{\overrightarrow{\omega }}^s$ 가 아니라 LOS 각속도 벡터인 $\overrightarrow{\mathrm{\Omega }}$ 이다. 식 (6)과 (12)에서

 

$$\begin{array}{r}\text{(13)}& {}^i{\overrightarrow{\omega }}^s\times {\hat{s}}_1& =({\omega }_1{\hat{s}}_1+\overrightarrow{\mathrm{\Omega }})\times {\hat{s}}_1\\ & =\overrightarrow{\mathrm{\Omega }}\times {\hat{s}}_1={\omega }_3{\hat{s}}_2\end{array}$$

 

이므로 식 (10)에서 미사일 가속도를 다음과 같이 구할 수 있다.

 

$$\begin{array}{}\text{(14)}& {\overrightarrow{a}}_{TPN}=N{V}_c\overrightarrow{\mathrm{\Omega }}\times {\hat{s}}_1,N>2\end{array}$$

 

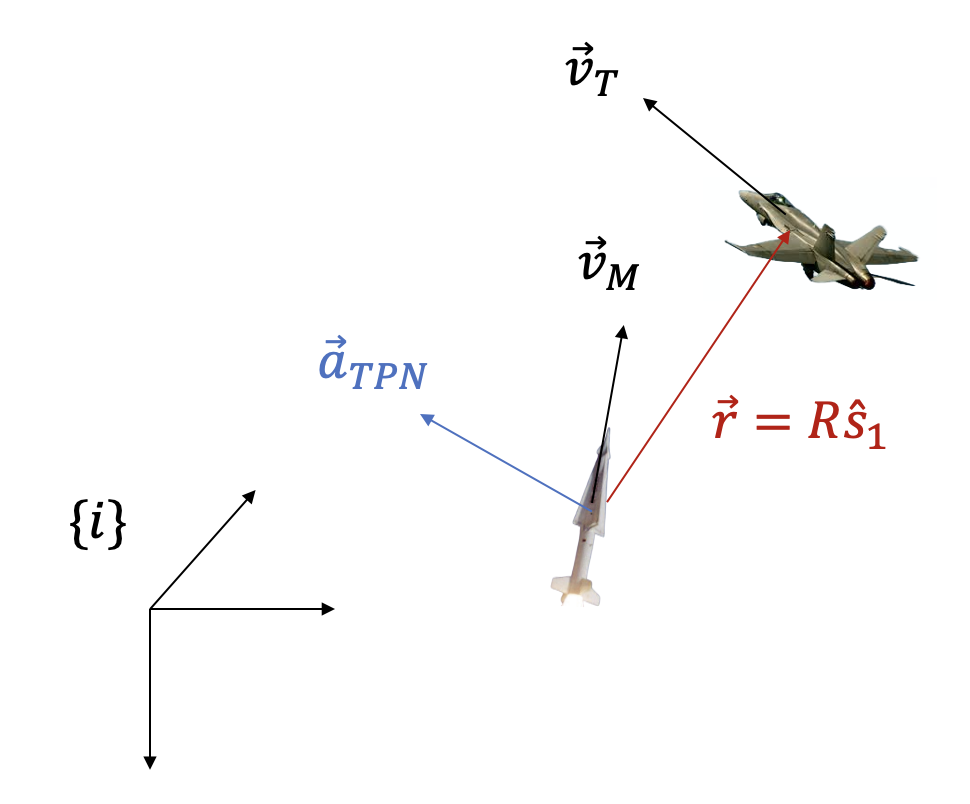
여기서 ${\overrightarrow{a}}_{TPN}$ 를 미사일 가속도 명령(acceleration command)이라고 하고 식 (14)를 참 PNG(TPNG, true proportional navigation guidance) 법칙이라고 한다. 식 (14)에 의하면 미사일 가속도 명령은 LOS에 수직이고 LOS 각속도 및 접근속력에 비례한다.

 

 

식 (14)를 식 (7)에 대입하고 LOS 단위벡터 방향의 성분을 구하면 다음과 같이 된다.

 

$$\begin{array}{}\text{(15)}& -{\overrightarrow{a}}_{TPN}\cdot {\hat{s}}_1=0=\ddot{R}-R{\omega }_3^2\end{array}$$

 

따라서 ${\omega }_3\to 0$ 이면 $\ddot{R}\to 0$ 이 되므로 $\dot{R}(0)<0$ 의 조건만 충족되면 TPNG 법칙은 표적을 요격하기 위한 충분조건을 만족한다.

TPNG 법칙에 의하면 미사일과 표적을 잇는 LOS가 변화하지 않으면, 즉 ${\omega }_3=0$ 이면 결국 미사일이 표적에 충돌하게 된다는 것을 말해준다.

미사일 가속도 명령은 공력 제어면(aerodynamic control surface)을 움직이거나 추력기(thruster) 또는 둘을 조합하여 물리적으로 구현한다.

공기역학적으로 제어되는 미사일의 경우 가속도 벡터는 LOS가 아니라 미사일 속도벡터에 거의 수직이고, 목표물에 대한 미사일의 접근속력도 기존 적외선 시커로는 측정할 수 없으며, 또한 엔진 스로틀링 기능이 없으면 미사일의 속도벡터 방향으로 가속할 수 없다. 이런 경우 TPNG를 적용하기는 힘들다.

하지만 PNG 법칙에는 TPNG 외에 변종인 순수 PNG(PPNG, pure proportional navigation guidance)라는 법칙이 있다. 이름으로 보면 PNG 법칙에서 진짜는 TPNG 하나라는 뜻인 것 같다. 그 변종인 PNG에 왜 순수(pure)라는 용어를 붙였는지는 모르겠으나 아마도 깊이 따지지 말고 순수하게 이용만 하라는 뜻인가 보다 (농담임).

PPNG 법칙은 식 (14)에서 접근속도 $V_c{\hat{s}}_1$ 대신에 미사일의 속도벡터를 사용한다.

 

$$\begin{array}{}\text{(16)}& {\overrightarrow{a}}_{PPN}=N\overrightarrow{\mathrm{\Omega }}\times {\overrightarrow{v}}_M\end{array}$$

 

TPNG가 LOS에 수직이고 LOS 각속도 및 접근속력에 비례하는 미사일 가속도 명령을 생성하는 반면, PPNG는 식 (16)에서 보듯이 미사일 속도벡터에 수직이며 LOS 각속도와 미사일 속도에 비례하는 미사일 가속도 명령을 생성한다.

 

 

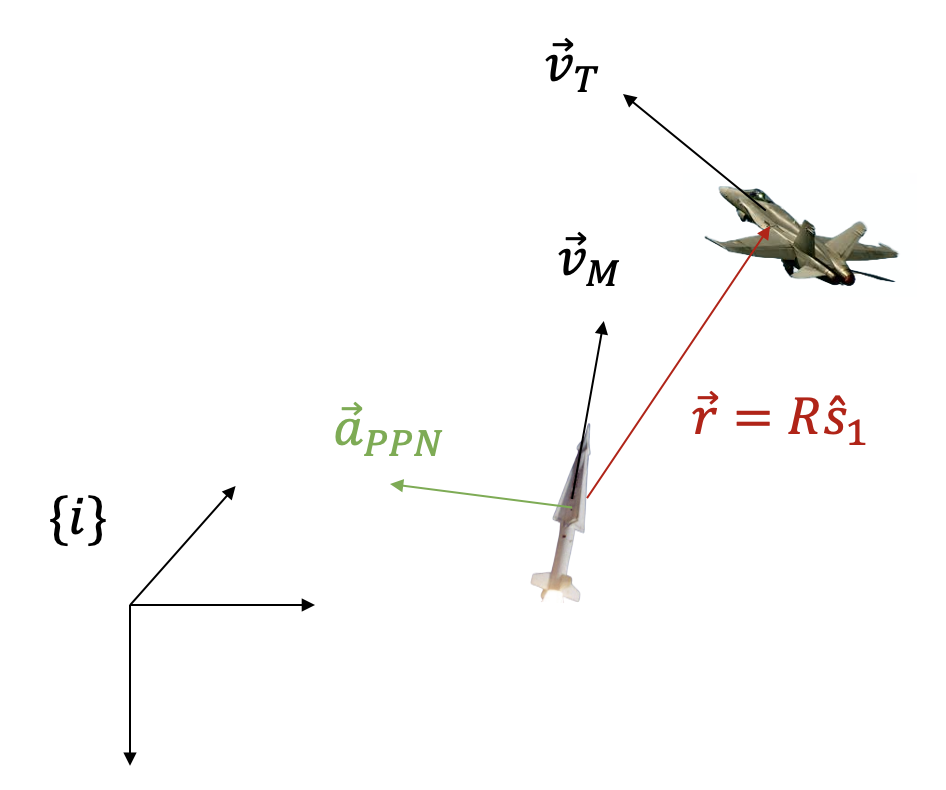
따라서 대기권 내 표적의 요격에는 TPNG보다 PPNG가 자연스럽게 더 선호되며, 대기권 외 요격에는 일반적으로 TPNG가 사용된다.

 

 

만약 중력의 영향을 고려해야 한다면 식 (14)와 (16)에서 중력 가속도를 보상해줘야 한다.

 

$$\begin{array}{r}\text{(17)}& & {\overrightarrow{a}}_{TPN}=N{V}_c\overrightarrow{\mathrm{\Omega }}\times {\hat{s}}_1-\overrightarrow{g}\\ & {\overrightarrow{a}}_{PPN}=N\overrightarrow{\mathrm{\Omega }}\times {\overrightarrow{v}}_M-{\overrightarrow{g}}_p\end{array}$$

 

여기서 ${\overrightarrow{g}}_p=\overrightarrow{g}-\frac{(\overrightarrow{g}\cdot {\overrightarrow{v}}_M){\overrightarrow{v}}_M}{|{\overrightarrow{v}}_M{|}^2}$ 로서 중력가속도 벡터에서 미사일 속도벡터 방향 성분을 뺀 것이다. PPNG가 미사일 속도벡터에 수직인 가속도 명령을 생성하는 것을 고려한 것이다.

PNG를 구현하려면 LOS 각속도 $\overrightarrow{\mathrm{\Omega }}$ 를 측정 또는 추정해야 하며, 이는 일반적으로 미사일의 시커 시스템이 담당한다. LOS 각속도의 참값은 수학적으로 다음과 같이 계산할 수 있다. 식 (1)과 (2)로부터

 

$$\begin{array}{r}\text{(18)}& \overrightarrow{r}\times \overrightarrow{v}& =R{\hat{s}}_1\times (\dot{R}{\hat{s}}_1+R^i{\overrightarrow{\omega }}^s\times {\hat{s}}_1)\\ & =R^2{\hat{s}}_1\times ({}^i{\overrightarrow{\omega }}^s\times {\hat{s}}_1)\\ \\ & =R^2({\hat{s}}_1\cdot {\hat{s}}_1{)}^i{\overrightarrow{\omega }}^s-R^2({\hat{s}}_1{\cdot }^i{\overrightarrow{\omega }}^s){\hat{s}}_1\end{array}$$

 

이므로 식 (12)를 이용하면 식 (18)은 다음과 같이 된다.

 

$$\begin{array}{r}\text{(19)}& \overrightarrow{r}\times \overrightarrow{v}& =R^2{\omega }_1{\hat{s}}_1+R^2\overrightarrow{\mathrm{\Omega }}-R^2({\omega }_1+{\hat{s}}_1\cdot \overrightarrow{\mathrm{\Omega }}){\hat{s}}_1\\ & =R^2\overrightarrow{\mathrm{\Omega }}\end{array}$$

 

따라서 식 (19)로 부터 LOS 각속도 벡터는 다음과 같이 계산된다.

 

$$\begin{array}{}\text{(20)}& \overrightarrow{\mathrm{\Omega }}=\frac{\overrightarrow{r}\times \overrightarrow{v}}{R^2}\end{array}$$