다음과 같이 제약조건이 없는 일반적인 최적화 문제가 있다.
\[ \min_{\mathbf{x}} f(\mathbf{x}) \ \ \ \ 또는 \ \ \ \ \max_{\mathbf{x}} f(\mathbf{x}) \]
여기서 \( \mathbf{x} \in R^n \)은 최적화 변수이고, \( f(\mathbf{x}) \)은 목적함수(objective function)이다. 이 목적함수를 최소화 또는 최대화하기 위한 조건은 무엇일까.
\( \mathbf{x} \)의 독립적 변화에 의해 유도된 함수 \( f(\mathbf{x}) \)의 변화량을 계산해 보자. \( \mathbf{x} \)의 변화량을 \( \Delta \mathbf{x} \)라고 하면, 함수의 증분(increment) \( \Delta f \)는 다음 식으로 주어진다.
\[ \Delta f = f(\mathbf{x}+ \Delta \mathbf{x} ) - f( \mathbf{x} ) \]
변화량이 매우 작을 때, 즉 \( \| \Delta \mathbf{x} \| → 0 \)일 때는 미분(differential) \( d \mathbf{x} \)로 표기하고 함수의 증분도 미분 \( df \)로 표기한다. 미분 \( df \)와 미분 \( d \mathbf{x} \)의 비율 \( \frac{df}{d \mathbf{x}} \)를 도함수(derivative)라고 한다 (흔히 이것도 미분이라고 번역한다).
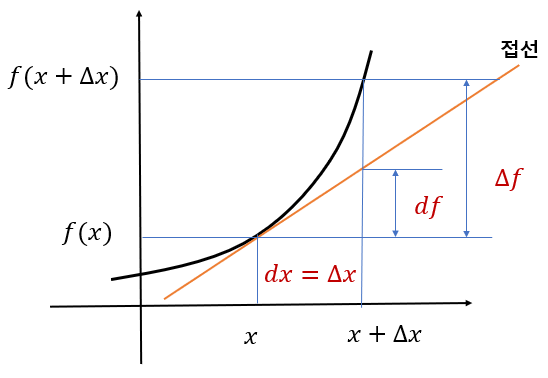
다음 그림은 최적화 변수가 스칼라일때의 함수의 증분과 미분 사이의 관계를 보여준다. 증분 \( \Delta f \)는 \( x \)의 변화량이 \( d x=\Delta x \)일 때 함수 \( f( x) \)의 변화량인 반면 \( df \)는 \( x \)점에서 계산한 접선(도함수)을 따라 생긴 변화량을 나타낸다. 즉 \( df= \frac{df}{d x} d x \)이다. 그래서 미분 \( df \)를 1차(first-order) 증분 또는 선형 증분이라고 한다.
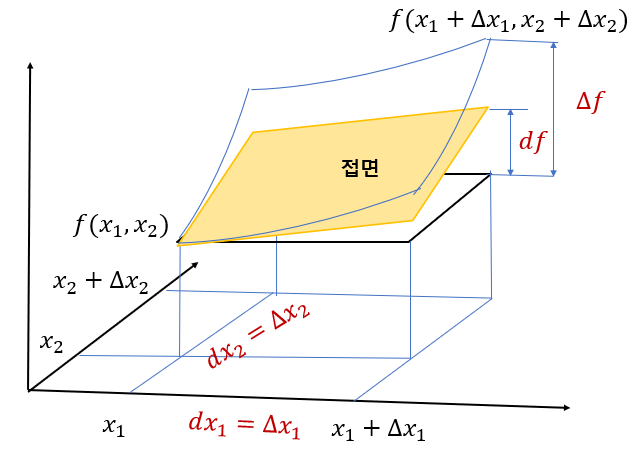
다음 그림은 최적화 변수가 2차원 벡터 \( \mathbf{x}= \begin{bmatrix} x_1 & x_2 \end{bmatrix}^T \)일 때의 함수의 증분과 미분 사이의 관계를 보여준다. 증분 \( \Delta f \)는 \( x_1 \)과 \( x_2 \)의 변화량이 각각 \( dx_1=\Delta x_1 \)과 \( dx_2=\Delta x_2 \)일 때 함수 \( f(\mathbf{x}) \)의 변화량인 반면, \( df \)는 \( x_1 \)과 \( x_2 \)점에서 계산한 접면(도함수)을 따라 생긴 변화량을 나타낸다. 즉
\[ d f = \frac{ \partial f}{\partial x_1} dx_1 + \frac{ \partial f}{\partial x_2} dx_2 \]
함수의 변수가 일반적인 \( n \)-차원 벡터 \( \mathbf{x} \)일 때의 함수의 미분 \( df \)는 다음과 같이 계산된다.
\[ \begin{align} d f &= \frac{ \partial f}{\partial x_1} dx_1 + \frac{ \partial f}{\partial x_2} dx_2 + \cdots + \frac{ \partial f}{\partial x_n} dx_n \\ \\ &= \left( \frac{df}{d \mathbf{x}} \right)^T d\mathbf{x} \end{align} \]
만약 \( \mathbf{x}^* \)을 기준으로 \( \| \mathbf{x}- \mathbf{x}^* \| < \epsilon \)을 만족하는 모든 \( \mathbf{x} \)에 대해서 \( \Delta f=f( \mathbf{x})-f( \mathbf{x}^* ) \ge 0 \)인 어떤 값 \( \epsilon > 0 \)가 존재한다면, \( f( \mathbf{x}^*) \)를 로컬 최소값이라고 하고, \( \Delta f= f(\mathbf{x})-f(\mathbf{x}^* ) \le 0 \)이라면 \( f( \mathbf{x}^*) \)를 로컬 최대값이라고 한다. 만약 \( \epsilon \)값을 임의의 큰 값으로 정할 수 있다면 각각 글로벌 최소값, 글로벌 최대값이라고 한다. 그리고 이 때의 \( \mathbf{x}^* \)를 정류점(stationary point) 또는 극점(extremal point)이라고 한다.
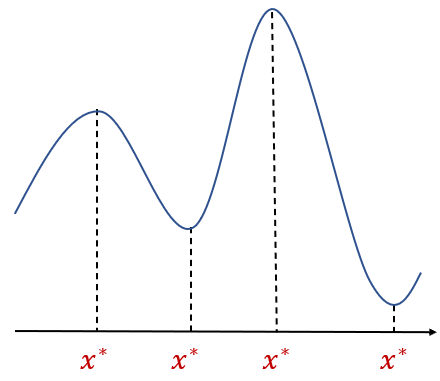
정류점에서는 함수의 미분이 0이 된다. 즉. \( df( \mathbf{x}^*)=0 \) 이다. 이 말은 어떤 함수가 어떤 값 \( \mathbf{x} \)에서 (로컬) 최소값 또는 최대값을 갖는다면 그 값이 바로 정류점이고 그 때 함수의 미분은 0이라는 뜻이다. 즉, 함수 \( f( \mathbf{x}) \)가 (로컬) 최소값 또는 최대값을 갖기 위한 필요조건은 다음과 같다.
\[ df( \mathbf{x}^* ) = 0 \]
증명해 보자.
먼저 함수가 \( \mathbf{x}^* \)에서 로컬 최소값을 갖는다면, \( \mathbf{x}= \mathbf{x}^*+ \alpha d \mathbf{x} \) 일 때 함수의 미분은 다음 식을 만족해야 한다.
\[ \begin{align} df( \mathbf{x}^* ) &= f(\mathbf{x}+\alpha d \mathbf{x}) - f(\mathbf{x}^*) \\ \\ &= \alpha \left( \frac{df}{d \mathbf{x}} \right)^T _{\mathbf{x}^*} d\mathbf{x} \ge 0 \end{align} \]
여기서 \( \alpha \gt 0 \)이고 \( ]|\alpha d \mathbf{x} \| → 0 \) 이며, \( \left( \frac{df}{d \mathbf{x}} \right)_{\mathbf{x}^*} \)는 \( \mathbf{x}=\mathbf{x}^* \)에서 계산한 \( \mathbf{x} \)에 대한 \( f \)의 그래디언트(gradient)이다. 또한 함수가 \( \mathbf{x}^* \)에서 로컬 최소값을 갖는다면, \( \mathbf{x}= \mathbf{x}^*-\alpha d \mathbf{x} \) 일 때도 다음 식을 만족해야 한다.
\[ \begin{align} df( \mathbf{x}^* ) &= f(\mathbf{x}- \alpha d \mathbf{x}) - f(\mathbf{x}^*) \\ \\ &= - \alpha \left( \frac{df}{d \mathbf{x}} \right)^T _{\mathbf{x}^*} d\mathbf{x} \ge 0 \end{align} \]
위 두 식에 의하면 동시에 \( \left( \frac{df}{d \mathbf{x}} \right)_{\mathbf{x}^*}^T d \mathbf{x} \ge 0 \) 과 \( \left( \frac{df}{d \mathbf{x} }\right)_{\mathbf{x}^*}^T d \mathbf{x} \le 0 \)을 만족해야 하므로, 함수가 \( \mathbf{x}^* \)에서 로컬 최소값을 갖는다면 \( \left( \frac{df}{d \mathbf{x}} \right)_{\mathbf{x}^*}^T d \mathbf{x} = 0 \) 또는 \( df( \mathbf{x}^* )=0 \)이 되야 한다.
동일한 방법을 사용하면 함수가 \( \mathbf{x}^* \)에서 로컬 최대값을 갖을 때에도 \( df( \mathbf{x}^* )=0 \)이 돼야 함을 증명할 수 있다.
정리하면, 함수 \( f( \mathbf{x}) \)가 \( \mathbf{x}^* \)에서 (로컬) 최소값 또는 최대값을 갖기 위한 필요조건은 다음과 같다.
\[ \begin{align} d f &= \left( \frac{df}{d \mathbf{x}} \right)^T d\mathbf{x} \\ \\ &= \frac{ \partial f}{\partial x_1} dx_1 + \frac{ \partial f}{\partial x_2} dx_2 + \cdots + \frac{ \partial f}{\partial x_n} dx_n \\ \\ &= 0 \end{align} \]
만약 \( \mathbf{x} \)의 성분이 모두 독립이라면, stationary point \( \mathbf{x}^* \)는 다음 식으로 계산할 수 있다.
\[ \frac{ \partial f}{\partial x_i} =0, \ \ \ \ i=1, 2, ... , n \]
'AI 수학 > 최적화' 카테고리의 다른 글
| 최소화의 필요조건과 충분조건 (0) | 2021.01.10 |
|---|---|
| SGD에서 데이터를 무작위로 추출해야 하는 이유 (1) | 2021.01.04 |
| 라그랑지 곱수법의 증명 (0) | 2020.10.01 |
| 라그랑지 곱수법 (0) | 2020.10.01 |
| 경사하강법 (0) | 2020.09.30 |




댓글