라그랑지 곱수(Lagrange multiplier)법은 등식 제약조건이 있는 최적화 문제를 풀기 위해 고안된 방법이다. 등식 제약조건이 있는 최적화 문제는 다음과 같다.
\[ \begin{align} & p^* = \min_{\mathbf{x}} f( \mathbf{x} ) \\ \\ subject \ to \ \ \ & h_j ( \mathbf{x} ) = 0, \ \ \ j=1,...,p \end{align} \]
여기서 \( \mathbf{x} \in R^n \) 은 최적화 변수, \( f( \mathbf{x}):R^n \to R \) 은 목적함수, \( h_j (\mathbf{x}):R^n \to R \) 은 등식 제약함수이다.
라그랑지 곱수법에 의하면 등식 제약조건이 있는 최적화 문제를 제약조건이 없는 최적화 문제로 바꿀 수 있다. 먼저 라그랑지안(Lagrangian)을 다음과 같이 정의하면,
\[ L (\mathbf{x}, \lambda_1, \lambda_2 , ... , \lambda_p ) = f( \mathbf{x}) + \lambda_1 h_1 (\mathbf{x}) + \lambda_2 h_2 (\mathbf{x}) + \cdots + \lambda_p h_p (\mathbf{x}) \]
원래 최적화 문제를 다음과 같이 제약조건이 없는 최적화 문제로 변환할 수 있다.
\[ p^* = \min_{\mathbf{x}, \lambda_1 , \lambda_2 , ... , \lambda_p} f( \mathbf{x}, \lambda_1 , \lambda_2 , ... , \lambda_p ) \]
여기서 \( \lambda_1 , \lambda_2 , ... , \lambda_p \)를 라그랑지 곱수라고 한다.
라그랑지 곱수법은 함수 값을 최소화하든 최대화하든 동일하게 사용된다.
예제를 풀어보자.
다음과 같이 가로 길이가 \( x \), 세로 길이가 \( y \), 높이가 \( z \)인 상자가 있다.
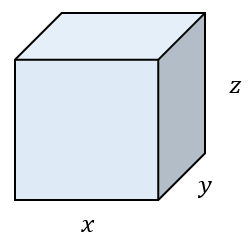
상자의 표면적이 \( c \)로 고정된 제약조건 하에서 상자의 부피가 최대가 되도록 상자의 가로, 세로, 높이를 계산하는 것이 문제다.
상자의 부피는 \( xyz \)이고, 상자의 표면적은 \( 2(xy+yz+xz) \)이므로 최적화 문제를 다음과 같이 수식으로 표현할 수 있다.
\[ \begin{align} & V^* = \min_{x,y,z} {f( x,y,z )=xyz} \\ \\ subject \ to \ \ \ & h_j (x,y,z) =xy+yz+xz-\frac{c}{2}= 0 \end{align} \]
위 최적화 문제를 풀기 위해서 라그랑지안을 다음과 같이 도입하면,
\[ L (x,y,z, \lambda) = xyz + \lambda (xy+yz+xz-\frac{c}{2} ) \]
원래 최적화 문제는 다음과 같이 제약조건이 없는 최적화 문제로 바꿀 수 있다.
\[ V^* = \min_{x,y,z, \lambda} { L( x,y,z, \lambda ) = xyz + (xy+yz+xz-\frac{c}{2} ) } \]
라그랑지안의 그래디언트를 계산해서 \( \triangledown L=0 \)으로 놓으면,
\[ \begin{align} \frac{\partial L}{\partial x} & = 0 = yz + \lambda (y+z) \\ \\ \frac{\partial L}{\partial y} & = 0 = xz + \lambda (x+z) \\ \\ \frac{\partial L}{\partial z} & = 0 = xy + \lambda (x+y) \\ \\ \frac{\partial L}{\partial \lambda} & = 0 = xy+yz +xz - \frac{c}{2} \end{align} \]
이 된다. 위 식을 풀면,
\[ x=y=z=\sqrt{\frac{c}{6}} \]
을 얻을 수 있다. 그 때의 상자의 부피는 \( V^*=\frac{c}{6} \sqrt{\frac{c}{6}} \)이다. 즉 동일한 표면적의 상자라면 정육면체가 부피가 제일 크다.
'AI 수학 > 최적화' 카테고리의 다른 글
| 함수의 최소화 또는 최대화의 조건 (0) | 2020.10.20 |
|---|---|
| 라그랑지 곱수법의 증명 (0) | 2020.10.01 |
| 경사하강법 (0) | 2020.09.30 |
| 최적화 문제의 분류 (0) | 2020.09.30 |
| 스칼라 함수를 벡터로 두번 미분하기 : 헤시안 (1) | 2020.07.17 |




댓글