제약조건이 없는 일반적인 최적화 문제는 다음과 같다.
\[ p^* = \min_{\mathbf{x}} f(\mathbf{x}) \]
또는,
\[ \mathbf{x}^* = \arg \min_{\mathbf{x}} f(\mathbf{x}) \]
여기서 \( \mathbf{x} \in R^n \) 은 최적화 변수이고, \( f(\mathbf{x}) \)은 목적함수(objective function)이다.
대부분 신경망 학습 알고리즘은 손실함수(loss function)를 정하거나 최적화를 위한 목적함수를 만드는 것으로 시작한다. 경사하강법(gradient descent) 또는 경사상승법(gradient ascent)은 목적함수를 최소화(minimization)하거나 최대화(maximization)하기 위해 신경망 학습 알고리즘에서 일반적으로 사용되는 최적화 방법이다.
경사하강법은 목적함수 \( f(\mathbf{x}) \)를 최소화하는 \( \mathbf{x} \)를 구하는 문제다. 경사상승법은 반대로 \( f(\mathbf{x}) \)를 최대화하는 \( \mathbf{x} \)를 구하는 문제다. \( f(\mathbf{x}) \)를 최대화하는 \( \mathbf{x} \)는 \( -f(\mathbf{x}) \)를 최소화하는 \( \mathbf{x} \)와 같으므로, 경사하강법과 경사상승법은 같은 문제라고 볼 수 있다.
경사하강법은 다음과 같이 직관적으로 이해할 수 있다. 아래 그림과 같은 일변수 함수 \( f(x) \)가 있다고 하자.
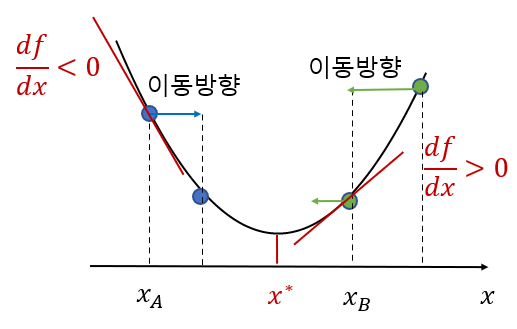
위치 \( x_A \)에서 최소값의 위치 \( x^* \)를 찾아가려면 우선 현재 위치에서의 목적함수 값 \( f(x_A) \)보다 작은 값을 갖는 방향으로 \( x \)를 움직여야 한다. 높은 곳에서 낮은 곳으로 방향을 잡아야 하므로 아래 방향으로 경사진 곳(경사하강)으로 이동해야 한다. 경사 또는 기울기는 \( x_A \)에서 \( f(x) \)의 미분(또는 접선의 기울기)을 계산하면 알 수 있다. 기울기가 음(\(-\))의 값이라면 양(\(+\))의 방향으로 \( x \)를 움직이면 된다. 만약 현재 위치가 \( x_B \)라면 기울기가 양(\(+\))의 값을 갖으므로 \( x \)를 음(\(-\))의 방향으로 움직여야 현재 위치보다 낮은 곳으로 이동할 수 있다. 이런 식으로 조금씩 아래 방향으로 \( x \)를 움직이다 보면 최소값의 위치 \( x^* \)에 도달할 수 있을 것이다.
이를 수식으로 쓰면 다음과 같다.
\[ x \gets x - \alpha \frac{df}{dx} \]
여기서 \( \alpha \gt 0 \)를 학습율(learning rate), 또는 스텝 사이즈(step size)라고 한다.
경사하강법은 일변수 뿐만 아니라 다변수 함수에도 적용할 수 있다. 경사하강법의 수식을 유도해 보도록 하자.
다변수 함수 \( f(\mathbf{x}) \)를 테일러 시리즈(Taylor series)로 전개하고 1차항에서 절삭하면 다음과 같다.
\[ f( \mathbf{x} + \eta \ \mathbf{d} ) \approx f( \mathbf{x}) + \triangledown_{\mathbf{x}} ^T f(\mathbf{x}) \eta \ \mathbf{d} \]
여기서 \( \mathbf{d} \in R^n \)은 크기가 1인 방향 벡터, \( \eta \gt 0 \)은 스칼라 변수다. \( \eta \)가 작을수록 1차 테일러 시리즈로 근사화한 값은 더 정확해진다. \( \triangledown_{\mathbf{x}} f( \mathbf{x} ) \)는 \( f(\mathbf{x}) \)의 그래디언트(gradient)로서 미분 \( \frac{df}{d \mathbf{x}} \)를 나타낸다.
\[ \triangledown_{\mathbf{x}} f(\mathbf{x}) = \frac{df}{d \mathbf{x}} = \begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots \\ \frac{\partial f}{\partial x_n} \end{bmatrix} \]
이제 \( f(\mathbf{x}+\eta \mathbf{d} ) \le f(\mathbf{x}) \)가 되도록 방향 벡터 \( \mathbf{d} \)를 계산해 보자. 방향 벡터 \( \mathbf{d} \)가 가리키는 방향으로 \( \mathbf{x} \)를 조금 이동시키면 함수의 값을 줄일 수 있을 것이다. 위 식에서
\[ \begin{align} f(\mathbf{x}) - f( \mathbf{x} + \eta \ \mathbf{d} ) & \approx -\triangledown_{\mathbf{x}} ^T f(\mathbf{x}) \eta \ \mathbf{d} \\ \\ &= -\cos \phi \ | \triangledown_{\mathbf{x}} f(\mathbf{x}) | \ \eta \end{align} \]
이므로, \( f(\mathbf{x})-f( \mathbf{x} + \eta \ \mathbf{d} ) \ge 0 \)을 최댓값으로 만드는 방향 벡터 \( \mathbf{d} \)를 구하면 된다. 여기서 \( \phi \)는 벡터 \( \triangledown_{\mathbf{x}} f(\mathbf{x}) \)와 \( \mathbf{d} \)의 사잇각이므로 최대화되기 위해서는 \( \phi = 180^0 \) 또는 \( \cos \phi = -1 \)이 되어야 한다. 즉 \( \mathbf{d} \)는 그래디언트 \( \triangledown_{\mathbf{x}} f(\mathbf{x}) \)의 정반대 방향이 되어야 한다.
\[ \mathbf{d} = - \frac{ \triangledown_{\mathbf{x}} f(\mathbf{x}) }{| \triangledown_{\mathbf{x}} f(\mathbf{x}) |} \]
따라서
\[ \begin{align} \mathbf{x} & \gets \mathbf{x} + \eta \ \mathbf{d} \\ \\ &= \mathbf{x}- \eta \frac{\triangledown_{\mathbf{x}} f(\mathbf{x})}{| \triangledown_{\mathbf{x}} f(\mathbf{x}) |} \\ \\ &= \mathbf{x}- \alpha \ \triangledown_{\mathbf{x}} f(\mathbf{x}) \end{align} \]
이면 \( f(\mathbf{x} + \eta \ \mathbf{d} ) \le f(\mathbf{x}) \)가 된다.
결국, 함수 \( f(\mathbf{x}) \)의 값을 줄이기 위한 \( \mathbf{x} \)의 이동 방향은 기울기 \( -\triangledown_{\mathbf{x}} f(\mathbf{x}) \)의 방향이다. 그 방향으로 \( \mathbf{x} \)를 조금씩 움직여 가며 함수 \( f(\mathbf{x}) \)를 계산하면 그 값이 점점 작아질 것이다. 물론 \( \triangledown_{\mathbf{x}} f(\mathbf{x}) = 0\)이 되는 지점에서 그 움직임이 멈출 것이므로 최종적으로 도착한 \( \mathbf{x} \)점이 글로벌 최소점(global minimum)임을 보장하지는 못한다. 목적함수가 컨벡스 함수가 아닐 경우에는 안장점(saddle point) 또는 지역 최솟값(local minimum)에 도달할 가능성도 있다.

참고로 안장점은 마치 말의 안장처럼 한쪽으로는 기울기가 상승되고 다른 쪽 방향으로는 기울기가 하강하는 평평한 지점을 말한다.

함수 \( f(\mathbf{x}) \)를 1차 테일러 시리즈로 근사화했다는 점을 상기하면 학습율 \( \alpha \)는 큰 값을 가지면 안 된다. 학습율 \( \alpha \)가 큰 값이면 \( f(\mathbf{x}) \)가 빠르게 최솟값으로 수렴할 수도 있지만 발산할 가능성이 크고, \( \alpha \)가 작으면 수렴 속도가 매우 느릴 것이므로, 학습율 \( \alpha \)는 너무 크지도 작지도 않아야 한다.
다음 그림은 학습율 \( \alpha \)를 크게 설정했기 때문에 \( x_1 \to x_2 \to \cdots \) 가 \( x^* \)에서 점점 멀어지고 있는 것을 보여준다.

'AI 수학 > 최적화' 카테고리의 다른 글
| 라그랑지 곱수법의 증명 (0) | 2020.10.01 |
|---|---|
| 라그랑지 곱수법 (0) | 2020.10.01 |
| 최적화 문제의 분류 (0) | 2020.09.30 |
| 스칼라 함수를 벡터로 두번 미분하기 : 헤시안 (1) | 2020.07.17 |
| 벡터 함수를 벡터로 미분하기 : 자코비안 (0) | 2020.07.16 |




댓글