다음과 같이 제약조건이 없는 일반적인 함수의 최적화 문제에서,
\[ \min_\mathbf{x} f(\mathbf{x}) \]
함수 \(f(\mathbf{x})\)가 \( \mathbf{x}^\star\)에서 로컬(local) 최소값이 되기 위한 필요조건(necessary condition)은 \( \mathbf{x}=\mathbf{x}^\star\)에서 계산한 \(f\)의 그래디언트(gradient)가 \(0\)이 되는 것이다.
\[ \nabla_\mathbf{x} f(\mathbf{x}^\star ) = 0 \]
위 조건을 \(\mathbf{x}^\star\)이 최소점이 되기 위한 1차(first order) 필요조건이라고 한다.
사실 위 조건은 로컬 최대점에서도 성립한다. 그럼 또 다른 필요조건이 필요할까, 그리고 충분조건(sufficient condition)은 무엇일까.
어떤 점 \(\mathbf{x}^\star\)를 기준으로 \(\lVert \mathbf{x}-\mathbf{x}^\star \rVert \le \epsilon \)을 만족하는 모든 \(\mathbf{x}\)에 대해서 \(f(\mathbf{x})-f(\mathbf{x}^\star ) \ge 0 \)인 어떤 값 \( \epsilon \gt 0\)이 존재한다면, \(\mathbf{x}^\star\)를 로컬 최소점이라고 한다.
로컬 최소점에서 가까운 점을 \(\mathbf{x}=\mathbf{x}^\star + \epsilon \mathbf{d}\)라고 할 때 \(f(\mathbf{x})\)를 \(\mathbf{x}^\star\)를 기준으로 테일러 시리즈로 전개하면 다음과 같다.
\[ \begin{align} f(\mathbf{x}) &= f(\mathbf{x}^\star + \epsilon \mathbf{d}) \\ \\ &=f( \mathbf{x}^\star ) + \epsilon \left( \nabla_\mathbf{x} f(\mathbf{x}^\star ) \right)^T \mathbf{d} + \frac{\epsilon ^2}{2} \mathbf{d}^T \nabla_\mathbf{x}^2 f(\mathbf{x}^\star ) \mathbf{d} + \mathcal{O} ( \epsilon^3) \end{align} \]
여기서 \(\nabla_\mathbf{x}^2 f(\mathbf{x}^\star )\)은 \( \mathbf{x}=\mathbf{x}^\star\)에서 계산한 \(\mathbf{x}\)에 대한 \(f\)의 헤시안(Hessian) 행렬이다. \(\nabla_\mathbf{x} f(\mathbf{x}^\star )=0\)이므로 극소 크기 \(\epsilon \gt 0\)에 대해서 위 식은 다음과 같이 된다.
\[ \frac{ f(\mathbf{x})-f(\mathbf{x}^\star) }{\epsilon^2 } = \frac{1}{2} \mathbf{d}^T \nabla_\mathbf{x}^2 f(\mathbf{x}^\star ) \mathbf{d} + \mathcal{O} ( \epsilon) \ge 0 \]
극한 \( \epsilon \to 0\)을 취하면 \( \mathbf{d}^T \nabla_\mathbf{x}^2 f(\mathbf{x}^\star ) \mathbf{d} \ge 0\)이 되므로
\[ \nabla_\mathbf{x}^2 f(\mathbf{x}^\star ) \ge 0 \]
이 되어야 한다. 즉 \(\mathbf{x}=\mathbf{x}^\star\)에서 계산한 \(\mathbf{x}\)에 대한 \(f\)의 헤시안이 준정정(positive semi-definite) 행렬이 되어야 한다.
따라서 \(\mathbf{x}^\star\)이 로컬 최소점이라면 다음 식이 성립한다.
\[ \begin{align} \nabla_\mathbf{x} f(\mathbf{x}^\star ) & = 0 \\ \\ \nabla_\mathbf{x}^2 f(\mathbf{x}^\star ) & \ge 0 \end{align} \]
위 식을 \(\mathbf{x}^\star\)가 최소점이 되기 위한 2차(second order) 필요조건이라고 한다.
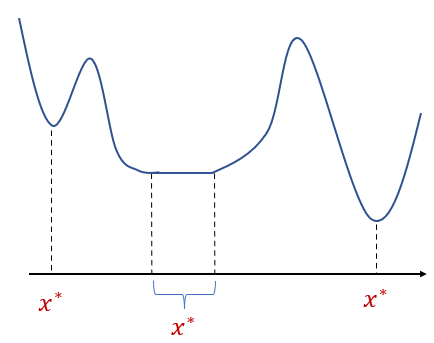
하지만 1차 필요조건과 2차 필요조건을 만족한다고 해서 \(\mathbf{x}^\star\)가 로컬 최소점이 된다는 보장은 없다. 아래 그림이 그 예다.

다시 테일러 시리즈를 이용하여 어떤 점 \(\mathbf{x}^\star\) 근방에서 \(f(\mathbf{x})\)를 전개해 보자.
\[ f(\mathbf{x}) - f(\mathbf{x}^\star) = \left( \nabla_\mathbf{x} f(\mathbf{x}^\star ) \right)^T (\mathbf{x}-\mathbf{x}^\star) + \frac{1}{2} (\mathbf{x}-\mathbf{x}^\star)^T \nabla_\mathbf{x}^2 f(\mathbf{x}^\star ) (\mathbf{x}-\mathbf{x}^\star) + \mathcal{O} ( \lVert \mathbf{x}-\mathbf{x}^\star \rVert^3 ) \]
여기서 \( \nabla_\mathbf{x} f(\mathbf{x}^\star )=0\)이고 \( \nabla_\mathbf{x}^2 f(\mathbf{x}^\star ) \)의 최소 고유값(eigenvalue)이 \( \lambda \gt 0\)이라면, 위 식은 다음과 같이 된다.
\[ \begin{align} f(\mathbf{x}) - f(\mathbf{x}^\star) & \ge \frac{\lambda}{2} \lVert \mathbf{x}-\mathbf{x}^\star \rVert^2 + \mathcal{O} ( \lVert \mathbf{x}-\mathbf{x}^\star \rVert^3 ) \\ \\ & = \left( \frac{\lambda}{2} + \mathcal{O} ( \lVert \mathbf{x}-\mathbf{x}^\star \rVert \right) \ \lVert \mathbf{x}-\mathbf{x}^\star \rVert^2 \end{align} \]
만약 \(\lVert \mathbf{x}-\mathbf{x}^\star \rVert \)가 매우 작다면 \( \frac{\lambda}{2}\)에 비해서 \( \mathcal{O} \left( \lVert \mathbf{x}-\mathbf{x}^\star \rVert \right) \)은 무시할 수 있으므로
\[ f(\mathbf{x}) - f(\mathbf{x}^\star) \ge 0 \]
이 된다. 따라서 다음과 같이 정리할 수 있다.
만약 어떤 점 \(\mathbf{x}^\star\)에서 다음 식이 성립하면,
\[ \begin{align} \nabla_\mathbf{x} f(\mathbf{x}^\star ) & = 0 \\ \\ \nabla_\mathbf{x}^2 f(\mathbf{x}^\star ) & \gt 0 \end{align} \]
\(\mathbf{x}^\star\)는 로컬 최소점이 된다. 위 식을 \(\mathbf{x}^\star\)가 최소점이 되기 위한 2차 충분조건이라고 한다.
여기서 \( \nabla_\mathbf{x}^2 f(\mathbf{x}^\star ) \)가 정정행렬(positive definite)이면, 즉 \( \nabla_\mathbf{x}^2 f(\mathbf{x}^\star ) \gt 0 \)이면 \( \nabla_\mathbf{x}^2 f(\mathbf{x}^\star ) \)의 모드 고유값이 양(plus)의 값임을 이용하였다.
'AI 수학 > 최적화' 카테고리의 다른 글
| [KKT 조건 - 2] KKT 조건과 적용 예제 (0) | 2021.01.18 |
|---|---|
| [KKT 조건 - 1] 등식과 부등식 제약조건이 있는 최적화 문제 (0) | 2021.01.14 |
| SGD에서 데이터를 무작위로 추출해야 하는 이유 (1) | 2021.01.04 |
| 함수의 최소화 또는 최대화의 조건 (0) | 2020.10.20 |
| 라그랑지 곱수법의 증명 (0) | 2020.10.01 |




댓글