램버트 정리 (Lambert’s theorem)

램버트(Lambert)는 궤도 운동을 하는 물체에 대한 두 지점 사이의 비행시간(time of flight)은 두 지점까지의 거리의 합, 두 지점을 직선으로 연결한 코드(chord) 길이, 궤도의 장반경만의 함수가 아닐까 생각했다. 나중에 라그랑지에 의해서 증명된 이 내용을 램버트 정리(Lambert's theorem)라고 한다.

램버트 정리는 케플러 방정식에서 도출할 수 있으며, 둘은 비슷한 문제를 푸는 관계라고 볼 수 있다. 케플러 방정식의 경우와 마찬가지로 램버트의 정리도 타원, 포물선, 쌍곡선의 세 가지 경우로 나뉜 램버트 방정식으로 표현되는데 수학적인 형식은 다음과 같다.

 

$$\begin{array}{}\text{(1)}& t_2-t_1=f(r_1+r_2,c,a)\end{array}$$

 

여기서 $r_1,r_2$ 는 궤도의 촛점(지구 중심)에서 두 지점까지의 거리, $c$ 는 코드 길이, $a$ 는 장반경이다.

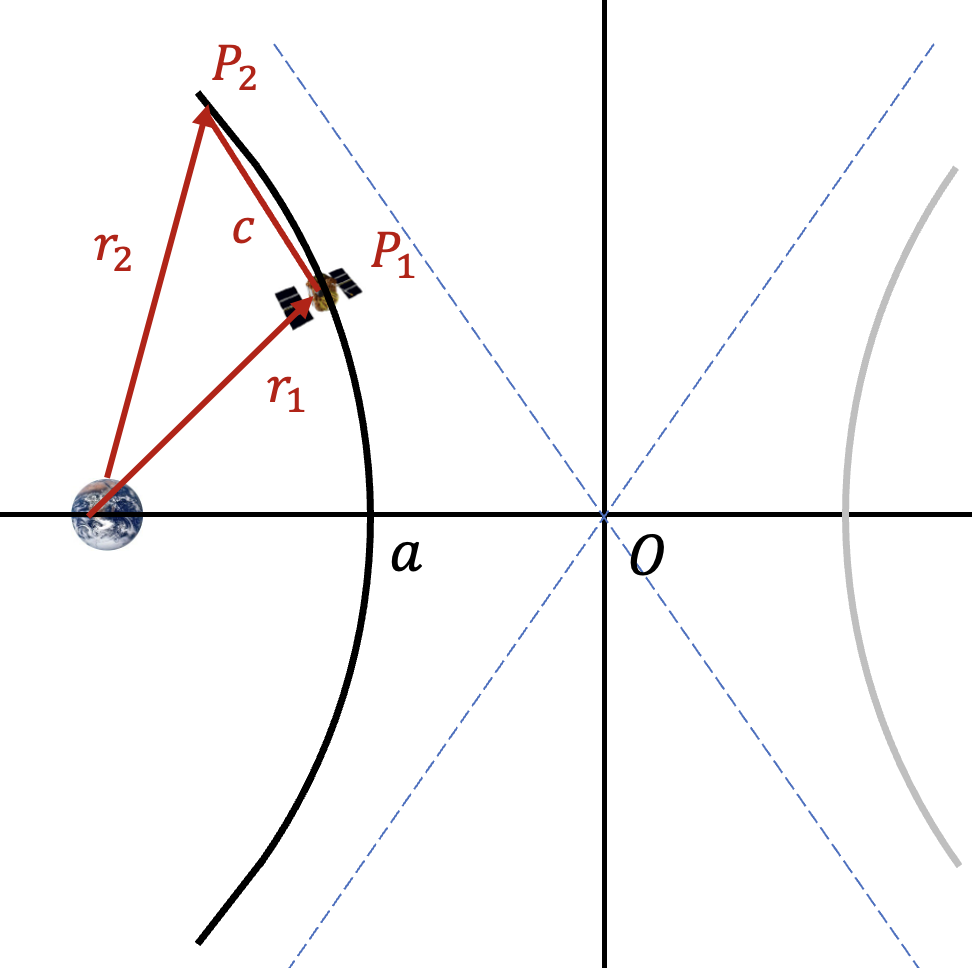
먼저 타원궤도에서 램버트 방정식을 유도해 보겠다.

 

 

그림에서 $x$ 축과 $y$ 축은 타원의 중심 $O$ 를 원점으로 하는 좌표축이다. 그러면 타원궤도를 돌고 있는 물체의 두 지점 $P_1$ 과 $P_2$ 의 위치는 다음과 같이 $x$ 축과 $y$ 축으로 표현할 수 있다.

 

$$\begin{array}{r}\text{(2)}& & x_1=a\cos E_1,x_2=a\cos E_2\\ & y_1=b\sin E_1,y_2=b\sin E_2\end{array}$$

 

여기서 $b$ 는 단반경(semi-minor axis)의 길이로서 이심율이 $e$ 인 경우 $b=a\sqrt{1-e^2}$ 으로 주어진다. 식 (2)를 이용하면 코드 길이 $c$ 는 다음과 같이 계산할 수 있다.

 

$$\begin{array}{r}\text{(3)}& c^2& =(x_1-x_2{)}^2+(y_1-y_2{)}^2\\ & =a^2(\cos E_1-\cos E_2{)}^2+a^2(1-e^2)(\sin E_1-\sin E_2{)}^2\end{array}$$

 

한편 두 지점 $P_1$ 과 $P_2$ 의 거리는 기하학적인 관계식을 이용하여 다음과 같이 계산할 수 있다.

 

$$\begin{array}{r}\text{(4)}& & r_1=a-ae\cos E_1\\ & r_2=a-ae\cos E_2\end{array}$$

 

따라서 두 거리의 합은 다음과 같다.

 

$$\begin{array}{}\text{(5)}& r_1+r_2=2a[1-\frac{1}{2}e(\cos E_1+\cos E_2)]\end{array}$$

 

타원궤도의 케플러 방정식(https://pasus.tistory.com/308)에 의하면 두 지점까지의 비행시간은 다음과 같이 주어진다.

 

$$\begin{array}{r}\text{(6)}& t_2-t_1& =\sqrt{\frac{a^3}{\mu }}(E_2-e\sin E_2-E_1+e\sin E_1)\\ & =\sqrt{\frac{a^3}{\mu }}[E_2-E_1-e(\sin E_2-\sin E_1)]\end{array}$$

 

식 (3), (5), (6)에 의하면 공통적으로 $a,e.E_1,E_2$ 의 함수이기 때문에 식 (1)의 형태로 종합할 수 있지 않을까 하는 생각이 들 것이다. 삼각함수의 덧셈이 등장하므로 일단 필요한 삼각함수 관계식을 모두 모아보겠다.

 

$$\begin{array}{r}\text{(7)}& & \cos d_2+\cos d_1=2\cos \left(\frac{d_2+d_1}{2}\right)\cos \left(\frac{d_2-d_1}{2}\right)\\ & \cos d_2-\cos d_1=-2\sin \left(\frac{d_2+d_1}{2}\right)\sin \left(\frac{d_2-d_1}{2}\right)\\ \\ & \sin d_2-\sin d_1=2\cos \left(\frac{d_2+d_1}{2}\right)\sin \left(\frac{d_2-d_1}{2}\right)\\ \\ & {\sin }^2\frac{d}{2}=\frac{1}{2}(1-\cos d)\end{array}$$

 

식 (7)을 적용하면 식 (3), (5), (6)은 각각 다음과 같이 쓸 수 있다.

 

$$\begin{array}{rl}\text{(8)}& & c^2=a^{2}4{\sin }^2\left(\frac{E_2+E_1}{2}\right){\sin }^2\left(\frac{E_2-E_1}{2}\right)& +a^2(1-e^2)4{\cos }^2\left(\frac{E_2+E_1}{2}\right){\sin }^2\left(\frac{E_2-E_1}{2}\right)\\ & =4a^2{\sin }^2\left(\frac{E_2-E_1}{2}\right)-4a^2{e}^2{\cos }^2\left(\frac{E_2+E_1}{2}\right){\sin }^2\left(\frac{E_2-E_1}{2}\right)\\ \\ & =4a^2{\sin }^2\left(\frac{E_2-E_1}{2}\right)[1-e^2{\cos }^2\left(\frac{E_2+E_1}{2}\right)]\\ \\ \text{(9)}& & r_1+r_2=2a[1-e\cos \left(\frac{E_2+E_1}{2}\right)\cos \left(\frac{E_2-E_1}{2}\right)]\\ \text{(10)}& & t_2-t_1=\sqrt{\frac{a^3}{\mu }}[E_2-E_1-2e\cos \left(\frac{E_2+E_1}{2}\right)\sin \left(\frac{E_2-E_1}{2}\right)]\end{array}$$

 

식 (8), (9), (10)을 보면 공통적인 항이 두 개가 보이는데 새로운 변수 $\kappa$ 와 $\gamma$ 를 도입하여 이를 간단히 표기하고자 한다.

 

$$\begin{array}{r}\text{(11)}& & \kappa =e\cos (\frac{E_2+E_1}{2})\\ & \gamma =\frac{1}{2}(E_2-E_1)\end{array}$$

 

그러면 식 (8), (9), (10)은 다음과 같이 간략히 표기된다.

 

$$\begin{array}{r}\text{(12)}& & c^2=4a^2{\sin }^2\gamma (1-{\kappa }^2)\\ \text{(13)}& & r_1+r_2=2a(1-\kappa \cos \gamma )\\ \text{(14)}& & t_2-t_1=\sqrt{\frac{a^3}{\mu }}[2\gamma -2\kappa \sin \gamma ]\end{array}$$

 

여기서 목표는 $\kappa$ 와 $\gamma$ 를 $r_1+r_2,c,a$ 의 관계식으로 만드는 것이다. 식 (12)와 (13)에 의하면,

 

$$\begin{array}{rl}\text{(15)}& r_1+r_2+c& =2a(1-\kappa \cos \gamma )+2a\sqrt{1-{\kappa }^2}\sin \gamma & =2a(1-\kappa \cos \gamma +\sqrt{1-{\kappa }^2}\sin \gamma )\\ \\ \text{(16)}& r_1+r_2-c& =2a(1-\kappa \cos \gamma )-2a\sqrt{1-{\kappa }^2}\sin \gamma & =2a(1-\kappa \cos \gamma -\sqrt{1-{\kappa }^2}\sin \gamma )\end{array}$$

 

이 된다. 식 (15)와 (16)의 패턴과 삼각함수 관계식 (7)을 유심히 살펴보면 다음과 같이 새로운 변수 ${\alpha }_e$ 와 ${\beta }_e$ 를 한번 더 도입하는 것이 식을 더 간단히 만들 수 있는 방법이라는 생각이 들 것이다.

 

$$\begin{array}{r}\text{(17)}& & \kappa =\cos \left(\frac{{\alpha }_e+{\beta }_e}{2}\right)\\ & \gamma =\frac{1}{2}({\alpha }_e-{\beta }_e)\end{array}$$

 

식 (17)을 식 (14), (15), (16)에 대입하면 다음과 같다.

 

$$\begin{array}{rl}\text{(18)}& & t_2-t_1=\sqrt{\frac{a^3}{\mu }}[({\alpha }_e-{\beta }_e)-2\cos \left(\frac{{\alpha }_e+{\beta }_e}{2}\right)\sin \left(\frac{{\alpha }_e-{\beta }_e}{2}\right)]& =\sqrt{\frac{a^3}{\mu }}[({\alpha }_e-\sin {\alpha }_e)-({\beta }_e-\sin {\beta }_e)]\\ \\ \text{(19)}& & r_1+r_2+c=2a(1-\cos {\alpha }_e)& =4a{\sin }^2\frac{{\alpha }_e}{2}\\ \\ \text{(20)}& & r_1+r_2-c=2a(1-\cos {\beta }_e)& =4a{\sin }^2\frac{{\beta }_e}{2}\end{array}$$

 

식 (19)와 (20)으로 부터

 

$$\begin{array}{r}\text{(21)}& \sin \frac{{\alpha }_e}{2}& =\sqrt{\frac{r_1+r_2+c}{4a}}=\sqrt{\frac{s}{2a}}\\ \sin \frac{{\beta }_e}{2}& =\sqrt{\frac{r_1+r_2-c}{4a}}=\sqrt{\frac{s-c}{2a}}\end{array}$$

 

를 얻을 수 있다. 여기서 $s=\frac{r_1+r_2+c}{2}$ 로서 삼각형 $P_{1}O{P}_2$의 둘레 길이의 반(semi-perimeter)이다.

식 (18)과 (21)은 식 (1)의 형태가 되며, 이를 타원궤도의 램버트 방정식이라고 한다. 램버트 방정식 (18)은 케플러 방정식 (6)과 유사해 보이지만 $E_1,E_2$ 와 ${\alpha }_e,{\beta }_e$ 는 서로 다른 변수이며, 케플러 방정식보다 풀기가 훨씬 어렵다.

 

 

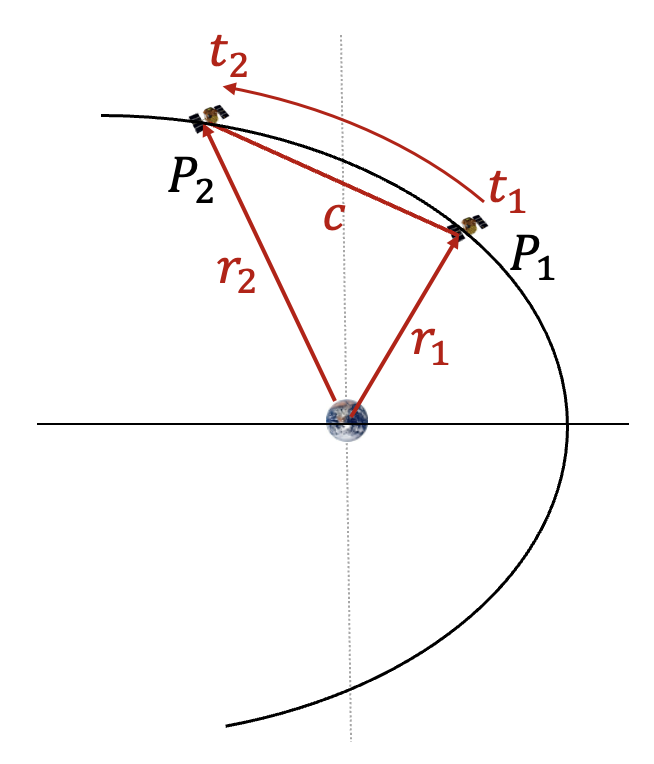
쌍곡선궤도에서도 타원궤도와 유사한 방법으로 램버트 방정식을 유도할 수 있다.

 

쌍곡선궤도의 케플러 방정식은 다음과 같이 주어진다 (https://pasus.tistory.com/309).

 

$$\begin{array}{}\text{(22)}& t_2-t_1=\sqrt{\frac{-a^3}{\mu }}(e\sinh F_2-F_2-e\sinh F_1+F_1),a<0\end{array}$$

 

두 지점 $P_1$ 과 $P_2$ 의 거리는 기하학적인 관계식을 이용하여 다음과 같이 계산할 수 있다.

 

$$\begin{array}{r}\text{(23)}& r_1& =-a(e\cosh F_1-1),a<0\\ r_2& =-a(e\cosh F_2-1)\end{array}$$

 

식 (22)와 (23)은 타원궤도와 쌍곡선궤도 수식의 유사성에 의해서도 유도될 수 있었다. 즉 식 (4)와 (6)에서 $jE\to -F$ 의 치환을 통하면 식 (23)과 (22)를 얻을 수 있다.

이와 같은 유사성을 바탕으로 식 (18)과 (21)은 다음과 같이 $\sin$ 함수를 $\sinh$ 함수로 바꾼 형태의 식으로 변환된다.

 

$$\begin{array}{r}\text{(24)}& & t_2-t_1=\sqrt{\frac{-a^3}{\mu }}[(\sinh {\alpha }_h-{\alpha }_h)-(\sinh {\beta }_h-{\beta }_h)],a<0\\ \text{(25)}& & \sinh \frac{{\alpha }_h}{2}=\sqrt{\frac{r_1+r_2+c}{-4a}}=\sqrt{\frac{s}{-2a}}\\ & \sinh \frac{{\beta }_h}{2}=\sqrt{\frac{r_1+r_2-c}{-4a}}=\sqrt{\frac{s-c}{-2a}}\end{array}$$

 

식 (24)와 (25)를 쌍곡선궤도의 램버트 방정식이라고 한다.

포물선궤도의 램버트 방정식은 타원궤도에서 장반경을 무한대로 늘려서, 즉 $a\to \mathrm{\infty }$ 로 놓으면 구할 수 있다.

 

 

식 (21)에 의하면 $a\to \mathrm{\infty }$ 일 때 ${\alpha }_e$ 와 ${\beta }_e$ 는 매우 작으므로 다음과 같은 근사식이 성립한다.

 

$$\begin{array}{r}\text{(26)}& & \sin {\alpha }_e\approx {\alpha }_e-\frac{1}{6}{\alpha }_e^3,\sin \frac{{\alpha }_e}{2}\approx \frac{{\alpha }_e}{2}\\ & \sin {\beta }_e\approx {\beta }_e-\frac{1}{6}{\beta }_e^3,\sin \frac{{\beta }_e}{2}\approx \frac{{\beta }_e}{2}\end{array}$$

 

식 (26)에서 $\sin {\alpha }_e\approx {\alpha }_e$ 로 근사하면 비행시간이 $0$ 이 되기 때문에 3차 테일러 항에서 절삭했다. 식 (26)을 식 (18)과 (21)에 대입하면 다음과 같이 된다.

 

$$\begin{array}{r}\text{(27)}& & \frac{{\alpha }_e}{2}=\sqrt{\frac{r_1+r_2+c}{4a}}=\sqrt{\frac{s}{2a}}\\ & \frac{{\beta }_e}{2}=\sqrt{\frac{r_1+r_2-c}{4a}}=\sqrt{\frac{s-c}{2a}}\\ \\ \text{(28)}& & t_2-t_1=\frac{1}{6}\sqrt{\frac{a^3}{\mu }}[{\alpha }_e^3-{\beta }_e^3]& =\frac{1}{6\sqrt{\mu }}[(r_1+r_2+c{)}^{3/2}-(r_1+r_2-c{)}^{3/2}]\\ & =\frac{1}{3}\sqrt{\frac{2}{\mu }}(s^{3/2}-(s-c{)}^{3/2})\end{array}$$

 

식 (28)을 포물선궤도의 램버트 방정식이라고 한다.

 

 

정리하면 각 궤도에서 램버트 방정식은 다음과 같다.

 

$$\begin{array}{rl}& \text{타원궤도:}\\ \\ & t_2-t_1=\sqrt{\frac{a^3}{\mu }}[({\alpha }_e-\sin {\alpha }_e)-({\beta }_e-\sin {\beta }_e)]\\ & \sin \frac{{\alpha }_e}{2}=\sqrt{\frac{r_1+r_2+c}{4a}}=\sqrt{\frac{s}{2a}}\\ & \sin \frac{{\beta }_e}{2}=\sqrt{\frac{r_1+r_2-c}{4a}}=\sqrt{\frac{s-c}{2a}}\\ \\ \\ & \text{쌍곡선궤도:}\\ \\ & t_2-t_1=\sqrt{\frac{-a^3}{\mu }}[(\sinh {\alpha }_h-{\alpha }_h)-(\sinh {\beta }_h-{\beta }_h)],a<0\\ & \sinh \frac{{\alpha }_h}{2}=\sqrt{\frac{r_1+r_2+c}{-4a}}=\sqrt{\frac{s}{-2a}}\\ & \sinh \frac{{\beta }_h}{2}=\sqrt{\frac{r_1+r_2-c}{-4a}}=\sqrt{\frac{s-c}{-2a}}\\ \\ \\ & \text{포물선궤도:}\\ \\ & t_2-t_1=\frac{1}{6\sqrt{\mu }}[(r_1+r_2+c{)}^{3/2}-(r_1+r_2-c{)}^{3/2}]\\ & =\frac{1}{3}\sqrt{\frac{2}{\mu }}(s^{3/2}-(s-c{)}^{3/2})\end{array}$$