케플러 문제 (Kepler’s problem) - 5

타원궤도, 포물선궤도, 쌍곡선궤도의 케플러 방정식을 이용하여 케플러 문제 (Kepler's problem)를 풀어보았는데(https://pasus.tistory.com/313). 이번에는 범용(universal) 케플러 방정식을 이용하여 케플러 문제를 풀어보도록 하겠다.

범용 케플러 방정식은 다음과 같았다. (https://pasus.tistory.com/310).

 

$$\begin{array}{}\text{(1)}& \sqrt{\mu }(t-t_0)=S(z){\chi }^3+\frac{{\overrightarrow{r}}_0\cdot {\overrightarrow{v}}_0}{\sqrt{\mu }}{\chi }^{2}C(z)+r_0\chi (1-zS(z))\end{array}$$

 

여기서 $z=\frac{{\chi }^2}{a}$ 이다.

범용변수(universal variable) $\chi$ 와 타원궤도의 이심 비행각 $E$, 포물선궤도의 실제 비행각 $\theta$, 그리고 쌍곡선궤도의 이심 비행각 $F$ 와의 관계식은 다음과 같다.

 

$$\begin{array}{r}\text{(2)}& \chi & =\sqrt{a}(E-E_0)\\ \chi & =\frac{h}{\sqrt{\mu }}(\tan \frac{\theta }{2}-\tan \frac{{\theta }_0}{2})\\ \\ \chi & =\sqrt{-a}(F-F_0)\end{array}$$

 

식 (2)에서 보듯이 범용변수 $\chi$ 는 각 궤도의 이심 비행각과 연결되어 있기 때문에 범용 '비행각' (universal anomaly)라고도 한다. 참고로 $\chi$ 의 단위는 $\sqrt{km}$ 이다.

 

 

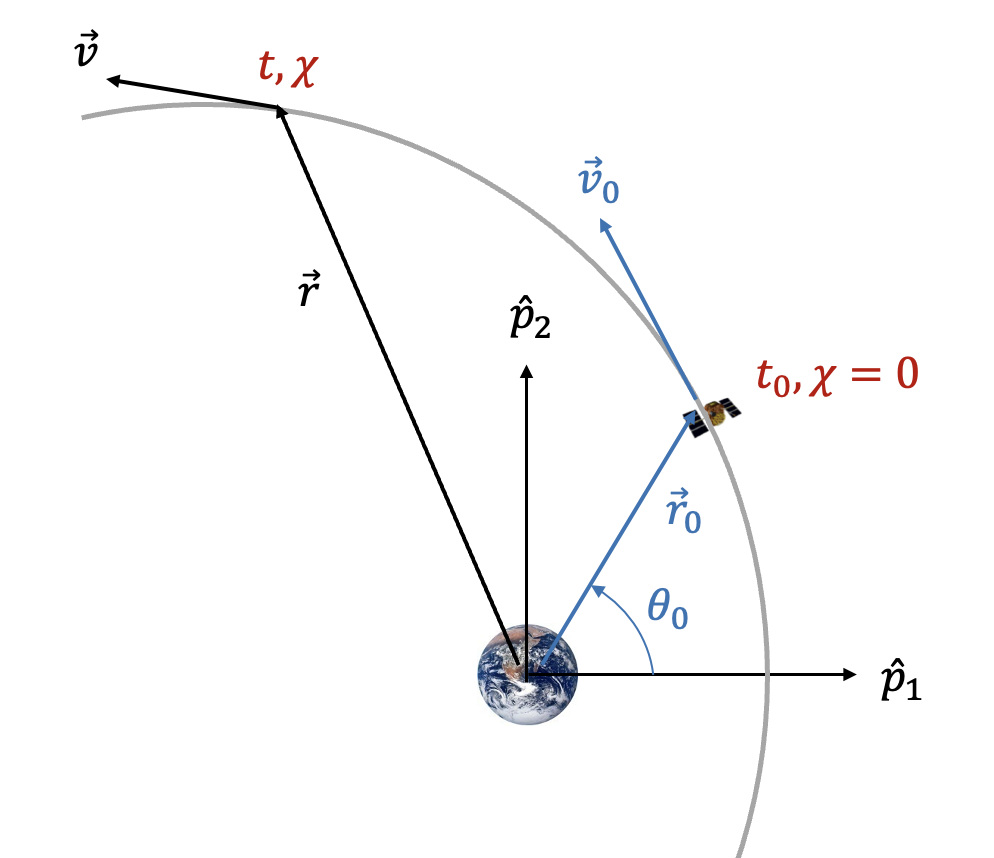
우주비행체의 위치벡터와 속도벡터가 시간 $t=t_0$ 에서 ${\overrightarrow{r}}_0,{\overrightarrow{v}}_0$ 로 주어졌을 때, 비행시간이 $t-t_0$ 만큼 경과한 후의 범용 비행각 $\chi$ 는 다음과 같은 순서로 계산할 수 있다.

[1] ${\overrightarrow{r}}_0$ 와 ${\overrightarrow{v}}_0$ 로부터 $r_0$ 와 장반경 $a$ 를 계산한다. 여기서 포물선궤도의 경우 $a=\mathrm{\infty }$ 이기 때문에 장반경 $a$ 의 역수인 $\alpha =\frac{1}{a}$ 를 사용하는 것이 편리하다.
[2] 식 (1)을 이용하여 비행시간 $t-t_0$ 에 대응하는 $\chi$ 를 계산한다.

범용 케플러 방정식 (1)은 비선형 방정식이므로 해석적으로 해를 구하기가 어렵기 때문에 수치적인 반복계산법으로 계산해야 한다. 뉴톤-랩슨 방법(Newton-Raphson method)을 이용하기 위해서 식 (1)을 다음과 같은 함수로 놓는다.

 

$$\begin{array}{r}\text{(3)}& f(\chi )& =S(z){\chi }^3+\frac{{\overrightarrow{r}}_0\cdot {\overrightarrow{v}}_0}{\sqrt{\mu }}{\chi }^{2}C(z)\\ & +r_0\chi (1-zS(z))-\sqrt{\mu }(t-t_0)\end{array}$$

 

$z=\frac{{\chi }^2}{a}=\alpha {\chi }^2$ 의 관계식을 이용하면 위 식을 다음과 같이 쓸 수 있다.

 

$$\begin{array}{rl}\text{(4)}& f(\chi )& =S(z){\chi }^3+\frac{{\overrightarrow{r}}_0\cdot {\overrightarrow{v}}_0}{\sqrt{\mu }}{\chi }^{2}C(z)& +r_0\chi (1-\alpha {\chi }^{2}S(z))-\sqrt{\mu }(t-t_0)\\ \\ & =\frac{{\overrightarrow{r}}_0\cdot {\overrightarrow{v}}_0}{\sqrt{\mu }}{\chi }^{2}C(z)+(1-\alpha r_0){\chi }^{3}S(z)+r_0\chi -\sqrt{\mu }(t-t_0)\end{array}$$

 

$|{\chi }_{i+1}-{\chi }_i|<ϵ$ 의 조건이 수렴할 때까지 다음식을 반복하여 업데이트 하기 위해서는

 

$$\begin{array}{}\text{(5)}& {\chi }_{i+1}={\chi }_i-\frac{f({\chi }_i)}{f^{\prime }({\chi }_i)}\end{array}$$

 

$f^{\prime }({\chi }_i)$ 을 계산해야 한다. $f^{\prime }({\chi }_i)$ 는 다음과 같이 계산할 수 있다.

 

$$\begin{array}{r}\text{(6)}& \frac{f(\chi )}{d\chi }& =2\frac{{\overrightarrow{r}}_0\cdot {\overrightarrow{v}}_0}{\sqrt{\mu }}\chi C(z)+\frac{{\overrightarrow{r}}_0\cdot {\overrightarrow{v}}_0}{\sqrt{\mu }}{\chi }^2\frac{dC(z)}{dz}\frac{dz}{d\chi }\\ & +3(1-\alpha r_0){\chi }^{2}S(z)+(1-\alpha r_0){\chi }^3\frac{dS(z)}{dz}\frac{dz}{d\chi }+r_0\end{array}$$

 

여기서

 

$$\begin{array}{r}\text{(7)}& \frac{dz}{d\chi }& =2\alpha \chi \\ \text{(8)}& \frac{dC(z)}{dz}& =-\frac{1}{z^2}-\frac{-z\left(\frac{1}{2\sqrt{z}}\right)\sin \sqrt{z}-\cos \sqrt{z}}{z^2}\\ & =\frac{1}{z^2}(-1+\frac{\sqrt{z}}{2}\sin \sqrt{z}+\cos \sqrt{z})\\ \\ & =\frac{1}{z^2}(-1+\frac{\sqrt{z}}{2}(\sqrt{z}-(\sqrt{z}{)}^{3}S(z))+(1-zC(z)))\\ \\ & =\frac{1}{2z}(1-zS(z)-2C(z))\\ \\ \text{(9)}& \frac{dS(z)}{dz}& =-\frac{1}{z^2}-\frac{(\sqrt{z}{)}^3\cos \sqrt{z}\left(\frac{1}{2\sqrt{z}}\right)-\left(\frac{3}{2}\sqrt{z}\right)\sin \sqrt{z}}{z^3}\\ & =\frac{1}{z^3}(-z-\frac{z}{2}\cos \sqrt{z}+\frac{3}{2}\sqrt{z}\sin \sqrt{z})\\ \\ & =\frac{1}{z^3}(-z-\frac{z}{2}(1-zC(z))+\frac{3}{2}\sqrt{z}(\sqrt{z}-(\sqrt{z}{)}^{3}S(z)))\\ \\ & =\frac{1}{2z}(C(z)-3S(z))\end{array}$$

 

이므로 식 (6)은 $z=\alpha {\chi }^2$ 임을 이용하면 다음과 같이 쓸 수 있다.

 

$$\begin{array}{r}\text{(10)}& \frac{f(\chi )}{d\chi }& =2\frac{{\overrightarrow{r}}_0\cdot {\overrightarrow{v}}_0}{\sqrt{\mu }}\chi C(z)\\ & +\frac{{\overrightarrow{r}}_0\cdot {\overrightarrow{v}}_0}{\sqrt{\mu }}{\chi }^2(\frac{1}{2\alpha {\chi }^2}(1-\alpha {\chi }^{2}S(z)-2C(z)))2\alpha \chi \\ \\ & +3(1-\alpha r_0){\chi }^{2}S(z)\\ \\ & +(1-\alpha r_0){\chi }^3(\frac{1}{2\alpha {\chi }^2}(C(z)-3S(z)))2\alpha \chi +r_0\\ \\ & =\frac{{\overrightarrow{r}}_0\cdot {\overrightarrow{v}}_0}{\sqrt{\mu }}\chi (1-\alpha {\chi }^{2}S(z))+(1-\alpha r_0){\chi }^{2}C(z)+r_0\end{array}$$

 

식 (5)에서 $\chi$ 의 초기값을 ${\chi }_0=\sqrt{\mu }|\alpha |(t-t_0)$ 로 하는 것이 일반적이다.

 

 

만약 범용 비행각으로부터 실제 비행각 $\theta$ 를 계산하고자 한다면, $\alpha$ 또는 $a$ 로 궤도의 모양을 판단하여 식 (2)로 궤도의 이심 비행각의 변화량을 계산해야 한다. 그런 후 다음 관계식을 이용하여 $\theta$ 를 계산하면 된다.

 

$$\begin{array}{r}\text{(11)}& & \tan \frac{E}{2}=\sqrt{\frac{1-e}{1+e}}\tan \frac{\theta }{2}\\ & \tanh \frac{F}{2}=\sqrt{\frac{e-1}{e+1}}\tan \frac{\theta }{2}\end{array}$$

 

$\alpha$ 는 다음과 같이 에너지 방정식으로부터 유도할 수 있다.

 

$$\begin{array}{}\text{(12)}& \alpha =\frac{1}{a}=\frac{2}{r_0}-\frac{v_0^2}{\mu }\end{array}$$

 

$\alpha >0$ 이면 타원궤도, $\alpha =0$ 이면 포물선궤도, $\alpha <0$ 이면 쌍곡선궤도이다.

초기 비행각 ${\theta }_0$ 는 ${\overrightarrow{r}}_0$ 와 ${\overrightarrow{v}}_0$ 를 이용하여 계산할 수 있다.

다음은 $\chi$ 의 계산 과정을 매트랩 코드로 구현한 것이다.

 

stumpff.m

 

function [Cz, Sz] = stumpff(z)

% [Cz, Sz] = stumpff(z)
%
% Stumpff functions
% coded by st.watermelon

eps = 1e-8;
if z > eps
    Cz = (1- cos(sqrt(z)))/z;
    Sz = (sqrt(z) - sin(sqrt(z)))/(sqrt(z))^3;

elseif z < -eps
    Cz = (cosh(sqrt(-z))-1)./(-z);
    Sz = (sinh(sqrt(-z))-sqrt(-z))/(sqrt(-z))^3;

else
    Cz = 1/2;
    Sz = 1/6;
    
end

 

universal_chi.m

 

function chi = universal_chi(r0_vec, v0_vec, tof)

% chi = universal_chi(r0_vec, v0_vec, tof)
%        given r0_vec, r0_vec and time-of-flight
%        compute universal alomaly chi
%       
% Input  r0_vec: initial position vector in km
%        v0_vec: initial velocity vector in km/sec
%        tof: time of flight in sec
% Output chi: universal anomaly in sqrt(km)
%
% all in inertial frame
%
% coded by st.watermelon

mu_e=398600; % gravitational parameter km^3/s^2


% step 1: compute r0 and a ---------------
r0 = sqrt(r0_vec'*r0_vec);
v0 = sqrt(v0_vec'*v0_vec);

alpha = 2/r0 - v0^2/mu_e; % alpha = 1/a 

% step 2 ----------------------------------

eps = 1e-8;

% compute chi
chi = sqrt(mu_e)*abs(alpha)*tof;
for ii = 1:100

    % Stumpff
    z = alpha * chi^2;
    [Cz, Sz] = stumpff(z);

    % Newton-Raphson
    f_chi = (r0_vec'*v0_vec)/sqrt(mu_e)*chi^2*Cz ...
             + (1-alpha*r0)*chi^3*Sz + r0*chi - sqrt(mu_e)*tof;
    dfdchi = (r0_vec'*v0_vec)/sqrt(mu_e)*chi*(1-alpha*chi^2*Sz) ...
             + (1-alpha*r0)*chi^2*Cz + r0;

    chi_next = chi - f_chi/dfdchi;

    if abs(chi_next-chi) < eps
        break;
    else
        chi = chi_next;
    end
   
end

 

 

 

만약 우주비행체의 초기 위치벡터 ${\overrightarrow{r}}_0$ 와 속도벡터 ${\overrightarrow{v}}_0$ 가 주어졌을 때, 비행시간이 $t-t_0$ 만큼 변화한 후의 위치벡터와 속도벡터 $\overrightarrow{r},\overrightarrow{v}$ 를 구하고자 한다면 범용변수와 라그랑지 계수(Lagrange coefficients)와의 관계식을 이용하면 된다.

라그랑지 계수는 다음과 같았다 (https://pasus.tistory.com/312).

 

$$\begin{array}{r}\text{(13)}& f& =1-\frac{{\chi }^2}{r_0}C(z)\\ g& =(t-t_0)-\frac{{\chi }^3}{\sqrt{\mu }}S(z)\\ \\ \text{(14)}& \dot{f}& =\frac{\sqrt{\mu }}{r{r}_0}\chi (zS(z)-1)\\ \dot{g}& =1-\frac{{\chi }^2}{r}C(z)\end{array}$$

 

위치벡터 및 속도벡터와 라그랑지 계수와의 관계식은 다음과 같았다 (https://pasus.tistory.com/311).

 

$$\begin{array}{r}\text{(15)}& \overrightarrow{r}& =f{\overrightarrow{r}}_0+g{\overrightarrow{v}}_0\\ \overrightarrow{v}& =\dot{f}{\overrightarrow{r}}_0+\dot{g}{\overrightarrow{v}}_0\end{array}$$

 

계산 순서는 다음과 같다.

[1] ${\overrightarrow{r}}_0$ 와 ${\overrightarrow{v}}_0$ 로부터 $r_0$ 와 장반경 $a$ 를 계산한다.
[2] $t-t_0$ 로부터 범용변수 $\chi$ 를 계산한다.
[3] 식 (13) 으로 라그랑지 계수 $f,g$ 를 계산한다.
[4] 식 (15) 로 $\overrightarrow{r}$ 를 계산한다. 그리고 $\overrightarrow{r}$ 의 크기인 $r$ 도 계산한다.
[5] 식 (14) 로 라그랑지 계수 $\dot{f},\dot{g}$ 를 계산한다.
[6] 식 (15) 로 $\overrightarrow{v}$ 를 계산한다.

다음은 위 알고리즘을 매트랩 코드로 구현한 것이다.

 

kepler_chi.m

 

function [r_vec, v_vec] = kepler_chi(r0_vec, v0_vec, tof)

% [r_vec, v_vec] = kepler_chi(r0_vec, v0_vec, tof)
%        given r0_vec, r0_vec and time-of-flight
%        compute r_vec and v_vec
%       
% Input  r0_vec: initial position vector in km
%        v0_vec: initial velocity vector in km/sec
%        tof: time of flight in sec
% Output r_vec: final position vector in km
%        v_vec: final velocity vector in km/sec
%
% all in inertial frame
%
% coded by st.watermelon

mu_e=398600; % gravitational parameter km^3/s^2

% step 1 : compute r0 and v0
r0 = sqrt(r0_vec'*r0_vec);
v0 = sqrt(v0_vec'*v0_vec);

alpha = 2/r0 - v0^2/mu_e; % alpha = 1/a 

% step 2 : compute chi
chi = universal_chi(r0_vec, v0_vec, tof);

% compute C(z), S(z) and z
z = alpha * chi^2;
[Cz, Sz] = stumpff(z);

% step 3 : Lagrange coefficients f and g
f = 1 - chi^2/r0 * Cz;
g = tof - chi^3/sqrt(mu_e)*Sz;

% step 4 : compute r_vec
r_vec = f*r0_vec + g*v0_vec;
r = sqrt(r_vec'*r_vec);

% step 5 : Lagrange coefficients f_dot and g_dot
f_dot = sqrt(mu_e)/(r*r0) * chi * (z*Sz-1);
g_dot = 1 - chi^2/r*Cz;

v_vec = f_dot*r0_vec + g_dot*v0_vec;