고전 궤도요소 (COE, classical orbital elements)의 6개 파라미터는 우주비행체의 위치벡터 및 속도벡터와 함수관계에 있다. 따라서 임의의 시간
우선 위치벡터와 속도벡터로부터 각운동량 벡터
다음은 위치벡터와 속도벡터로부터 각운동량 벡터, 승교선 벡터, 이심율 벡터를 구하는 방법에 대한 설명이다.
각운동량 벡터
각운동량 벡터
로 구하면 된다. 각운동량 벡터는 전 궤도상에서 상수로 유지되므로 모든
승교선 벡터
승교선 벡터는 적도면과 궤도면의 교차선과 평행하며 크기는 각운동량과 같고 방향은 지구중심에서 우주비행체가 지구의 남반구에서 북반구로 올라가면서 만나는 점을 향하는 벡터이다. 적도면과 직각인 벡터는

이심율 벡터
이심율 벡터는 크기가 이심율

궤적방정식 유도 과정 (https://pasus.tistory.com/102)에 의하면 다음 식이 있었다.
여기서
로 놓을 수 있다.
가 된다.
이 된다.
다음은 각운동량 벡터
통반경
이심율은 이심율 벡터의 크기이고, 통반경은 정의에 의하여 구하면 된다. 장반경은 포물선궤도를 제외하고는
여기서

경사각
경사각은
RAAN
RAAN은
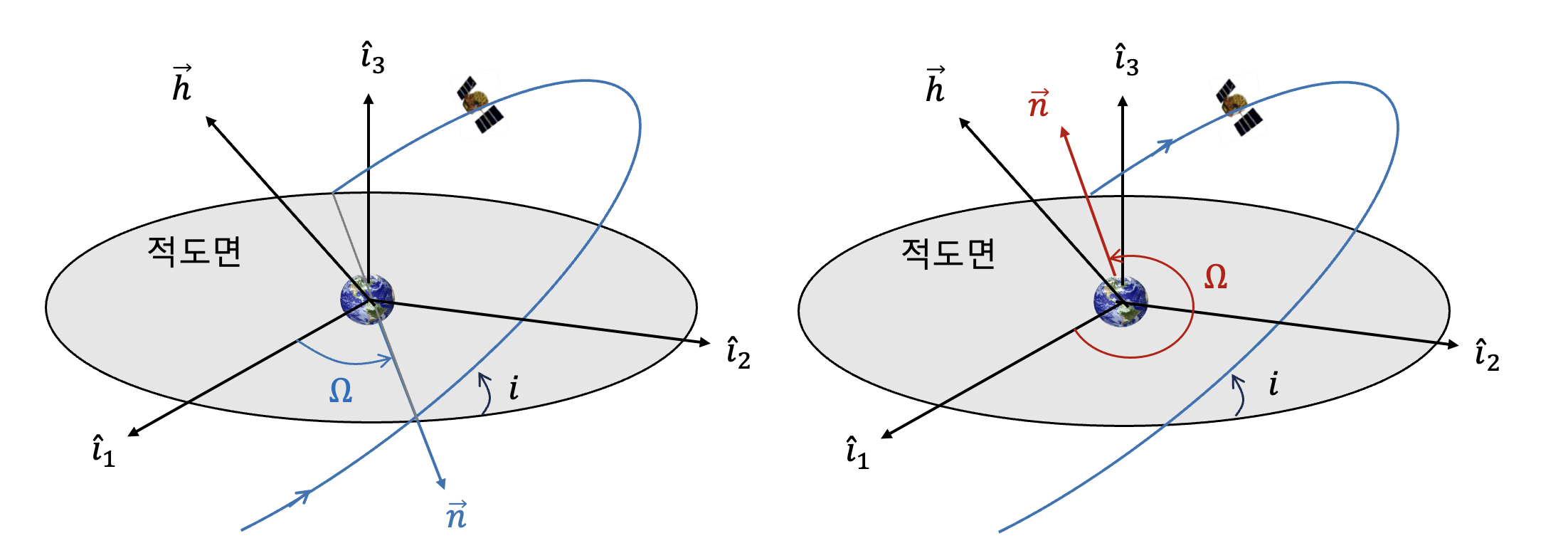
RAAN은
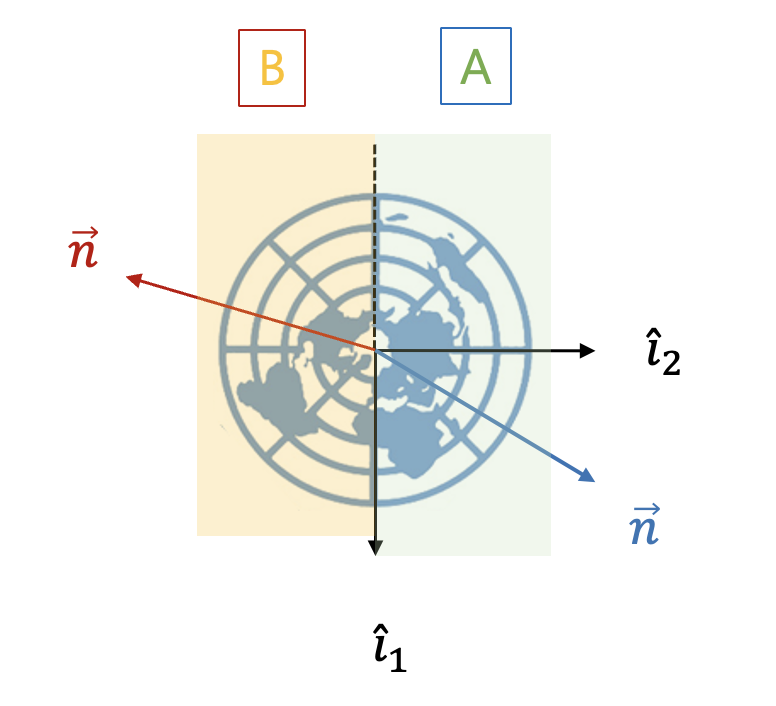
적도궤도인 경우
근점편각
근점편각은
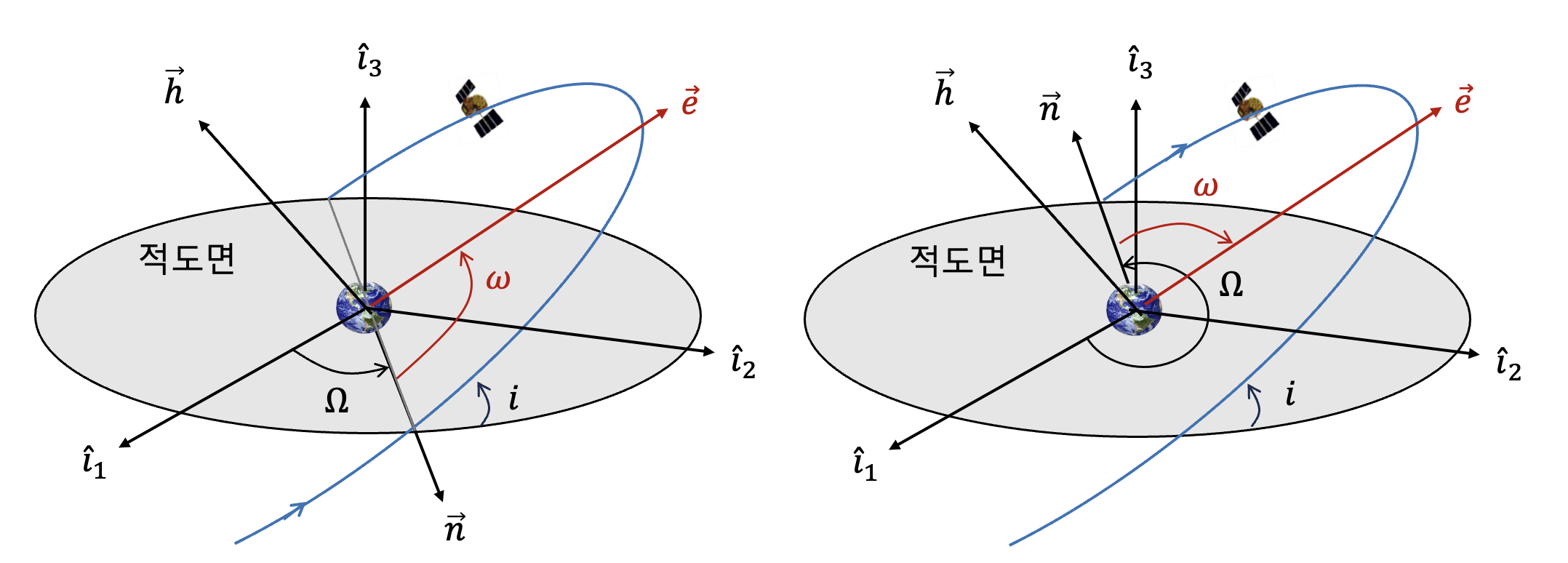
근점편각은 궤도의 운동방향으로 측정해야 한다. RAAN 과 마찬가지로 식 (10)으로 계산한 근점편각도 0도에서 180도의 범위밖에 계산하지 못하므로 부호를 구별할 수 있는 정보가 더 필요하다. 아래 그림의 A영역에서는 근점편각이
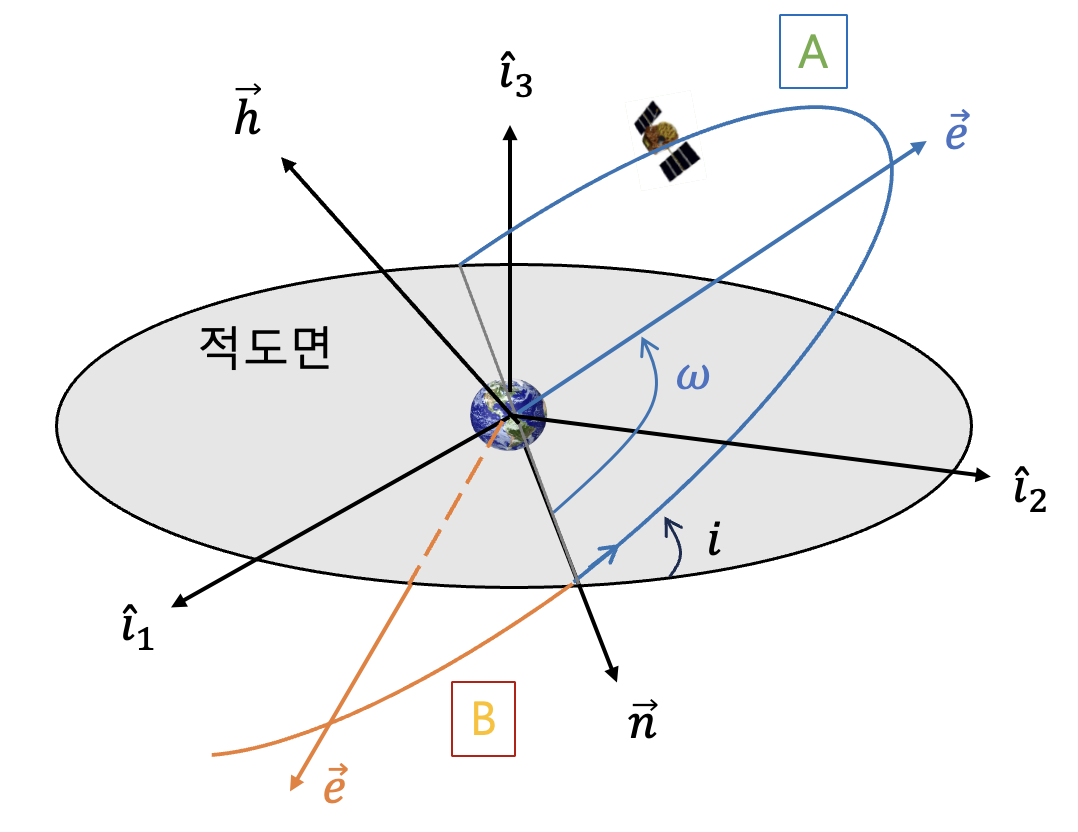
적도궤도인 경우
다음 그림의 A영역에서는 근점편각이
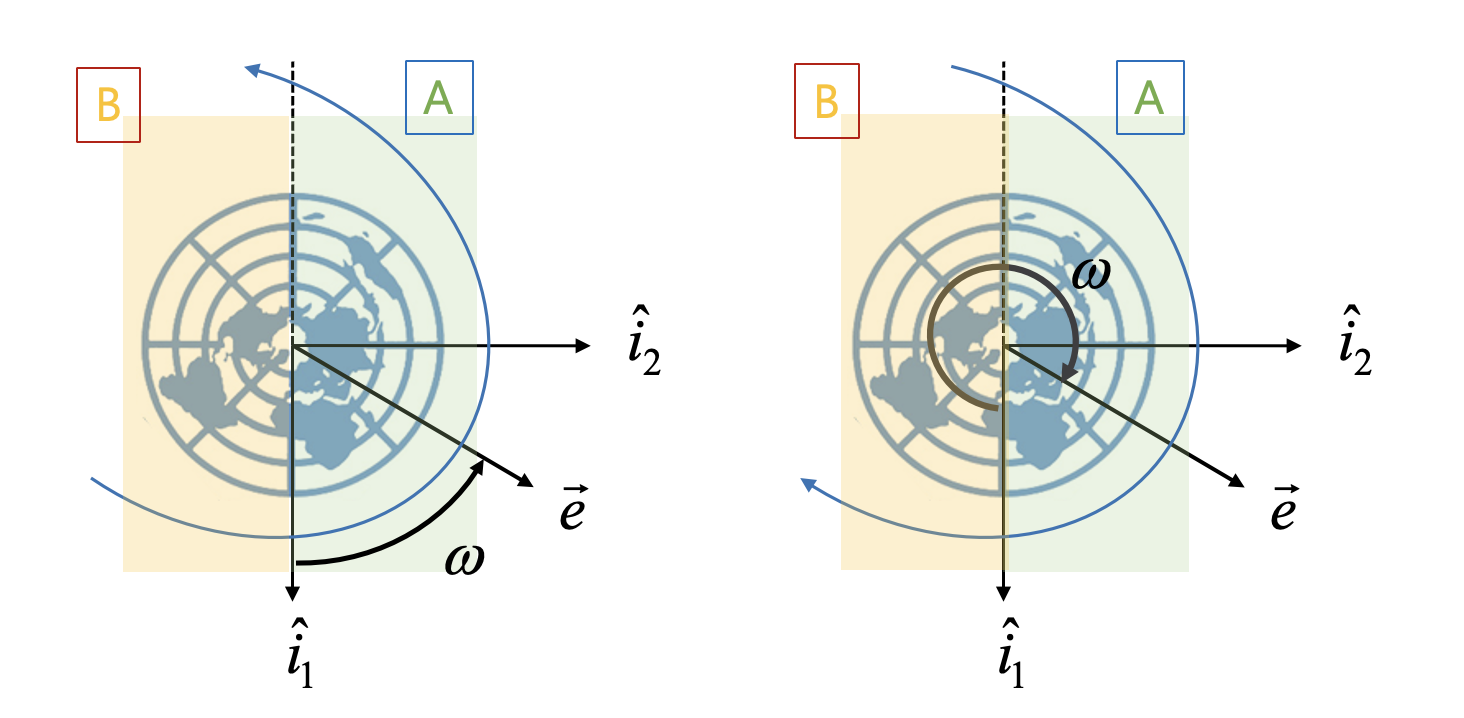
원궤도인 경우
실제비행각
실제비행각은 위치벡터
실제비행각은
실제비행각은 궤도의 운동방향으로 측정해야 한다. 다음 그림의 A영역에서는 실제비행각이
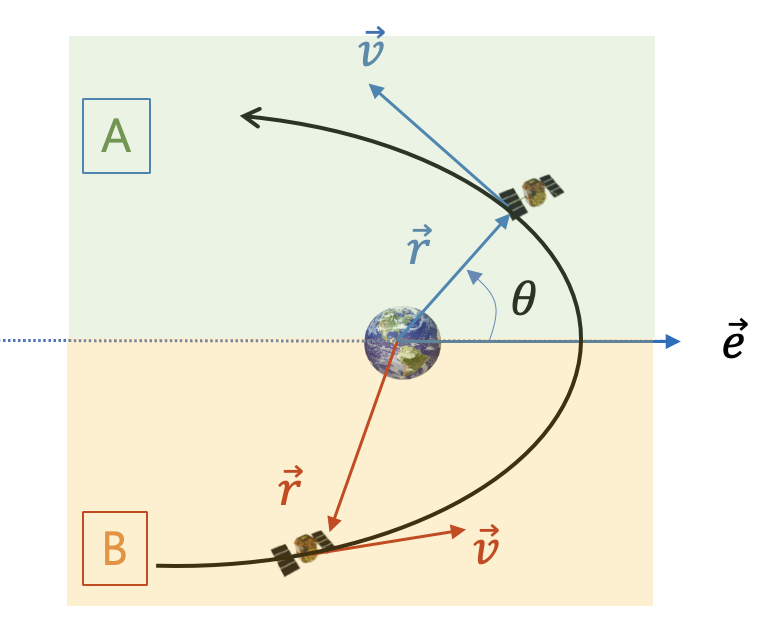
원궤도인 경우
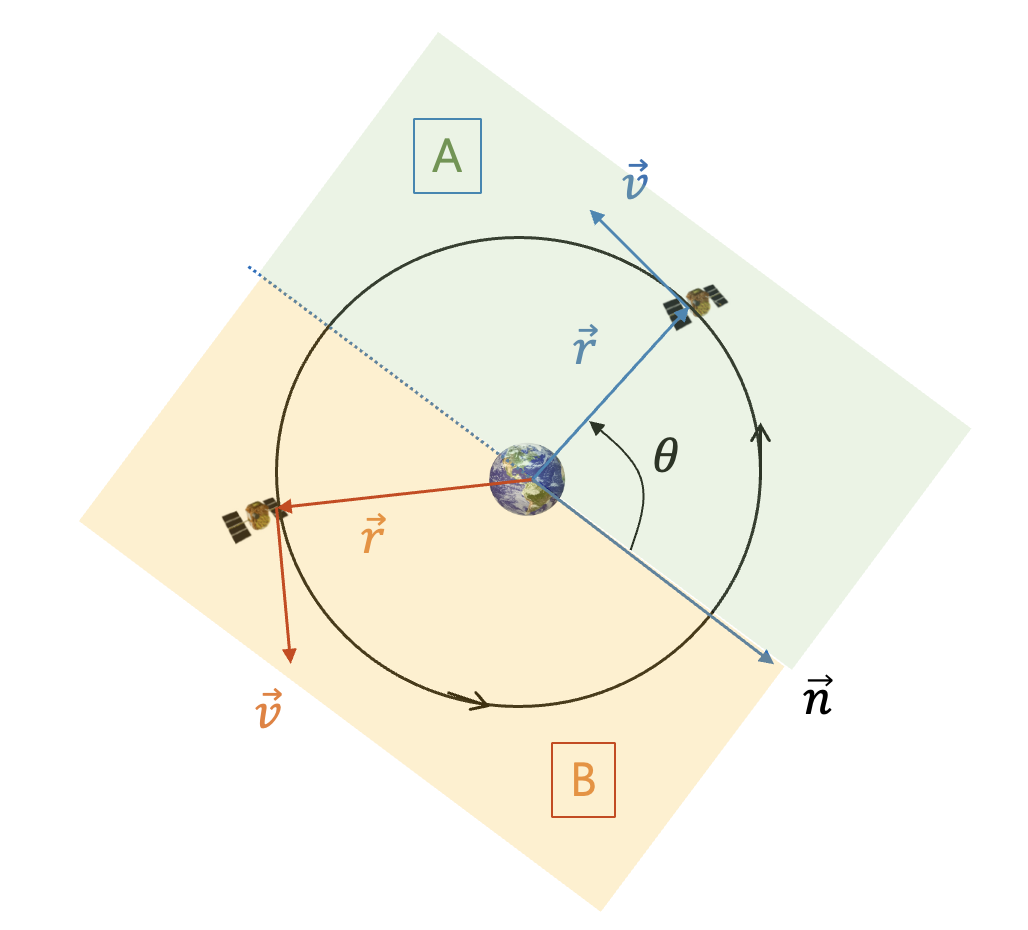
다음 그림의 A영역에서는 실제비행각이
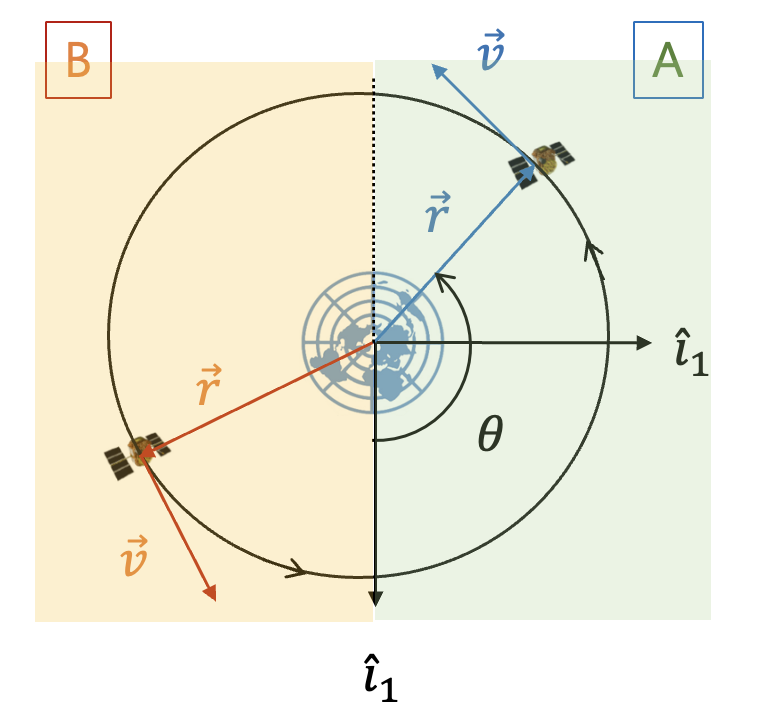
원궤도이면서 적도궤도인 경우
다음 그림의 A영역에서는 실제 비행각이
예를 들어서, 어떤 싯점에서 우주비행체의 위치벡터와 속도벡터가 다음과 같이 주어졌다면,
궤도요소
다음은 위치벡터와 속도벡터를 고전 궤도요소로 변환해 주는 매트랩 코드다.
function [a,es,ii,W,w,theta] = rv2coe(r,v)
% [a,e,i,W,w,theta] = rv2coe(r,v)
% Converting vectors R and V in inertial frame to orbit elements,
% where V=dR/dt in inertial frame.
% Input (R, V) in km, km/sec
% Output (a, e, i, W, w, theta) in (km, sec) and degrees (p=a(1-e^2))
% equatorial orbit: W=0, w is angle between (i_1) and perigee
% circular orbit: w=0, theta is angle between ascending node and R
% equatorial and circular orbit: W=w=0, theta is angle between (i_1) and R
%
% coded by st.watermelon
Req = 6378.137; % km Earth radius
e_er = 0.0818191908426; % Earth eccentricity
mu=398600; % gravitational parameter km^3/s^2
% angular momentum, ascending node and eccentricity vectors
h = cross(r,v);
n = cross([0 0 1]',h);
ev = ((v'*v-mu/norm(r))*r-(r'*v)*v)/mu;
%
p = h'*h/mu; % semi-latus rectum
es = norm(ev); % eccentricity
ns = norm(n);
ii = acos([0 0 1]*h/(norm(h)))*180/pi; % inclination
a = p/(1-es^2);
eps = 1e-8;
if abs(ii)<=eps | abs(ii-180)<=eps % equatorial orbit
W=0;
if abs(es)>eps % equatorial, but NOT circular orbit
w = acos([1 0 0]*ev/es)*180/pi;
if ([0 1 0]*ev<0) w = -w; end
if (abs((ii-180))<=eps) w = -w; end
theta = acos(ev'*r/(es*norm(r)))*180/pi;
if (r'*v<0) theta = -theta; end
else % euqatorial and circular orbit
w = 0;
theta = acos([1 0 0]*r/(nomr(r)))*180/pi;
if ([1 0 0]*v>0) theta = -theta; end
end
else % NOT equatorial orbit
W = acos([1 0 0]*n/ns)*180/pi;
if ([0 1 0]*n<0) W = -W; end
if abs(es)>eps % NOT circular orbit
w = acos(n'*ev/(ns*es))*180/pi;
if ([0 0 1]*ev<0) w = -w; end
theta=acos(ev'*r/(es*norm(r)))*180/pi;
if (r'*v<0) theta = -theta; end
else % circular orbit
w = 0;
theta = acos(n'*r/(ns*norm(r)))*180/pi;
if (n'*v>0) theta = -theta; end
end
end
'항공우주 > 우주역학' 카테고리의 다른 글
| [CR3BP] 주기궤도의 매니폴드 계산 (0) | 2023.08.01 |
|---|---|
| 궤도요소 (COE)로 부터 위치 및 속도벡터 계산 (0) | 2023.07.31 |
| 고전 궤도요소 (Classical Orbital Elements) (0) | 2023.07.24 |
| [CR3BP] 주기궤도의 안정성 (0) | 2023.07.22 |
| [CR3BP] 헤일로 궤도 (Halo Orbit) 계산 (0) | 2023.07.14 |




댓글