[CR3BP] 주기궤도의 안정성

어떤 $\overline{\mathbf{x}}(t)$ 가 다음 미분방정식의 해로 주어지는 주기(period)가 $T$ 인 주기궤도라고 하자.

 

$$\begin{array}{}\text{(1)}& \dot{\overline{\mathbf{x}}}(t)=\mathbf{f}(\overline{\mathbf{x}}(t))\end{array}$$

 

$\overline{\mathbf{x}}(t)$ 에 약간의 섭동 $\delta \mathbf{x}(t)$ 을 주고 식 (1)에 대입한 후 테일러 시리즈 1차 근사식을 구하면 다음과 같이 된다.

 

$$\begin{array}{rl}& \dot{\overline{\mathbf{x}}}(t)+\delta \dot{\mathbf{x}}(t)\approx \mathbf{f}(\overline{\mathbf{x}}(t))+{\frac{\partial \mathbf{f}}{\partial \mathbf{x}}|}_{\overline{\mathbf{x}}(t)}\delta \mathbf{x}(t)\\ \\ \text{(2)}& \to & \delta \dot{\mathbf{x}}(t)=A(t)\delta \mathbf{x}(t)\end{array}$$

 

$\overline{\mathbf{x}}(t)$ 가 주기함수이므로 $A(t)$ 도 주기함수다.

 

$$\begin{array}{}\text{(3)}& A(t)=A(t+T)\end{array}$$

 

 

한편 식 (2)의 기본행렬 $\mathrm{\Psi }(t)$ 는 다음과 같다 (https://pasus.tistory.com/274).

 

$$\begin{array}{}\text{(4)}& \frac{d}{dt}\mathrm{\Psi }(t)=A(t)\mathrm{\Psi }(t),\mathrm{\Psi }(t_0)=I\end{array}$$

 

여기서 $A(t)$ 가 주기함수이므로 다음과 같은 상수 비특이행렬(non-singular matrix) $M$ 이 존재한다.

 

$$\begin{array}{}\text{(5)}& \mathrm{\Psi }(t+T)=\mathrm{\Psi }(t)M\end{array}$$

 

여기서 $M$ 을 모노드로미 행렬(monodromy matrix)이라고 하며 다음과 같이 주어진다.

 

$$\begin{array}{}\text{(6)}& M={\mathrm{\Psi }}^{-1}(t)\mathrm{\Psi }(t+T)=\mathrm{\Phi }(t+T,t)\end{array}$$

 

여기서 $\mathrm{\Phi }(t,\tau )$ 는 상태천이행렬(state transition matrix)로서 다음 미분방정식을 만족한다.

 

$$\begin{array}{}\text{(7)}& \frac{d}{dt}\mathrm{\Phi }(t,\tau )=A(t)\mathrm{\Phi }(t,\tau ),\mathrm{\Phi }(\tau ,\tau )=I\end{array}$$

 

또한 두 싯점간의 상태변수를 매핑해 준다.

 

$$\begin{array}{}\text{(8)}& \delta \mathbf{x}(t)=\mathrm{\Phi }(t,\tau )\delta \mathbf{x}(\tau )\end{array}$$

 

 

 

식 (6)과 (8)에 의하면,

 

$$\begin{array}{r}\text{(9)}& \delta \mathbf{x}(t_0+kT)& =\mathrm{\Phi }(t_0+kT,t_0+(k-1)T)\delta \mathbf{x}(t_0+(k-1)T)\\ & =M\delta \mathbf{x}(t_0+(k-1)T)\\ \\ & =M\mathrm{\Phi }(t_0+(k-1)T,t_0+(k-2)T)\delta \mathbf{x}(t_0+(k-2)T)\\ \\ & =M^2\delta \mathbf{x}(t_0+(k-2)T)\\ \\ & \cdots \\ \\ & =M^k\delta \mathbf{x}(t_0)\end{array}$$

 

이므로 주기궤도 $\overline{\mathbf{x}}(t)$ 의 안정성(stability)은 모노드로미 행렬 $M$ 의 고유값(eigenvalue)에 달려있다. 모노드로미 행렬의 고유값 ${\mu }_i$ 을 Floquet multipliers 라고 한다. 고유값이 $|{\mu }_j|<1$ 이면 궤도의 섭동은 $0$ 으로 수렴할 것이고 $|{\mu }_j|>1$ 이면 발산할 것이다. 참고로 Floquet exponents ${\gamma }_j$ 는 다음과 같이 Floquet multipliers의 로그값으로 정의한다.

 

$$\begin{array}{}\text{(10)}& {\gamma }_j=\frac{1}{T}\log {\mu }_j\end{array}$$

 

이제 라그랑지 포인트(Langrage point)에서의 주기함수의 모노드로미 행렬의 고유값을 구해보도록 하자. 라그랑지 포인트에서의 주기궤도의 선형화 미분방정식은 식 (2)로 주어지며 그 때의 상태변수는 다음과 같다 (https://pasus.tistory.com/280).

 

$$\begin{array}{}\text{(11)}& \delta \mathbf{x}(t)=[\delta x\delta y\delta z\delta v_x\delta v_y\delta v_z{]}^T\end{array}$$

 

한편 원궤도제한 삼체문제(CR3BP)의 운동 방정식은 해밀톤(Hamilton) 방정식으로도 유도할 수 있다 (https://pasus.tistory.com/158). 일반화 좌표 $\mathbf{q}$ 와 일반화 운동량 $\mathbf{p}$ 를 다음과 같이 정의하고,

 

$$\begin{array}{}\text{(12)}& \mathbf{q}=\left[\begin{array}{c}{q}_1\\ q_2\\ q_3\end{array}\right]=\left[\begin{array}{c}x\\ y\\ z\end{array}\right],\mathbf{p}=\left[\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right]=\left[\begin{array}{c}\dot{x}-y\\ \dot{y}+x\\ \dot{z}\end{array}\right]\end{array}$$

 

해밀토니안 함수(Hamiltonian function)를 다음과 같이 정의한다면,

 

$$\begin{array}{}\text{(13)}& H=\frac{1}{2}((p_1+y{)}^2+(p_2-x{)}^2+p_3^2)+U_{eff}\end{array}$$

 

해밀톤 표준 방정식에 의해서 CR3BP의 운동 방정식을 얻을 수 있다 (https://pasus.tistory.com/147).

 

$$\begin{array}{r}\text{(14)}& \dot{\mathbf{q}}& =\frac{\partial H}{\partial \mathbf{p}}=\left[\begin{array}{c}{p}_1+y\\ p_2-x\\ p_3\end{array}\right]\\ \dot{\mathbf{p}}& =-\frac{\partial H}{\partial \mathbf{q}}=\left[\begin{array}{c}{p}_2-x-{\overline{U}}_x\\ -p_1-y-{\overline{U}}_y\\ -{\overline{U}}_z\end{array}\right]\end{array}$$

 

식 (14)를 상태변수 $\mathbf{z}=\left[\begin{array}{c}\mathbf{q}\\ \mathbf{p}\end{array}\right]$ 의 방정식으로 표현하면 다음과 같다.

 

$$\begin{array}{r}\text{(15)}& \dot{\mathbf{z}}& =\left[\begin{array}{c}\dot{\mathbf{q}}\\ \dot{\mathbf{p}}\end{array}\right]=\left[\begin{array}{cc}0& I\\ -I& 0\end{array}\right]\left[\begin{array}{c}\frac{\partial H}{\partial \mathbf{q}}\\ \frac{\partial H}{\partial \mathbf{p}}\end{array}\right]\\ & =\left[\begin{array}{cc}0& I\\ -I& 0\end{array}\right]\frac{\partial H}{\partial \mathbf{z}}\end{array}$$

 

위 식으로부터 기준 주기궤도 $\overline{\mathbf{z}}$ 에서의 선형화 미분방정식을 다음과 같이 얻을 수 있다.

 

$$\begin{array}{}\text{(16)}& \delta \dot{\mathbf{z}}=J\frac{\partial }{\partial \mathbf{z}}\left(\frac{\partial H}{\partial \mathbf{z}}\right)\delta \mathbf{z}=JS(\overline{\mathbf{z}})\delta \mathbf{z}\end{array}$$

 

여기서

 

$$J=\left[\begin{array}{cc}0& I\\ -I& 0\end{array}\right],S(\overline{\mathbf{z}})=\frac{\partial }{\partial \mathbf{z}}\left(\frac{\partial H}{\partial \mathbf{z}}\right)$$

 

이다. 선형 미분방정식 (16)의 상태천이행렬 $\tilde{\mathrm{\Phi }}(t,\tau )$ 는 다음과 같이 구할 수 있다.

 

$$\begin{array}{}\text{(17)}& \frac{d}{dt}\tilde{\mathrm{\Phi }}(t,\tau )=JS(\overline{\mathbf{z}})\tilde{\mathrm{\Phi }}(t,\tau )\end{array}$$

 

그리고 시간 $t$ 의 상태변수 $\delta \mathbf{z}(t)$ 는 다음과 같이 계산할 수 있다.

 

$$\begin{array}{}\text{(18)}& \delta \mathbf{z}(t)=\tilde{\mathrm{\Phi }}(t,t_0)\delta \mathbf{z}(t_0)\end{array}$$

 

 

 

이제 상태천이행렬 $\tilde{\mathrm{\Phi }}(t,t_0)$ 가 심플렉틱 행렬(symplectic matrix)이라는 것을 증명하려고 한다 (https://pasus.tistory.com/275). 먼저 행렬 $U(t)$ 를 다음과 같이 정의한다.

 

$$\begin{array}{}\text{(19)}& U(t)={\tilde{\mathrm{\Phi }}}^T(t,t_0)J\tilde{\mathrm{\Phi }}(t,t_0),U(t_0)=J\end{array}$$

 

위 식을 미분하면 식 (17)에 의해서 다음과 같이 된다.

 

$$\begin{array}{r}\text{(20)}& \dot{U}(t)& ={\dot{\tilde{\mathrm{\Phi }}}}^T(t,t_0)J\tilde{\mathrm{\Phi }}(t,t_0)+{\tilde{\mathrm{\Phi }}}^T(t,t_0)J\dot{\tilde{\mathrm{\Phi }}}(t,t_0)\\ & ={\tilde{\mathrm{\Phi }}}^T(t,t_0)S(\overline{\mathbf{z}})J^{T}J\tilde{\mathrm{\Phi }}(t,t_0)+{\tilde{\mathrm{\Phi }}}^T(t,t_0)JJS(\overline{\mathbf{z}})\tilde{\mathrm{\Phi }}(t,t_0)\\ \\ & ={\tilde{\mathrm{\Phi }}}^T(t,t_0)S(\overline{\mathbf{z}})\tilde{\mathrm{\Phi }}(t,t_0)-{\tilde{\mathrm{\Phi }}}^T(t,t_0)S(\overline{\mathbf{z}})\tilde{\mathrm{\Phi }}(t,t_0)\\ \\ & =0\end{array}$$

 

따라서

 

$$\begin{array}{}\text{(21)}& U(t)={\tilde{\mathrm{\Phi }}}^T(t,t_0)J\tilde{\mathrm{\Phi }}(t,t_0)=J\end{array}$$

 

이기 때문에 $\tilde{\mathrm{\Phi }}(t,t_0)$ 는 심플렉틱 행렬이다. 심플렉틱 행렬의 특성 (https://pasus.tistory.com/275)에 의해서 $\tilde{\mathrm{\Phi }}(t,t_0)$ 의 행렬식(determinant)은 항상 $1$ 이고, $\lambda$ 가 $\tilde{\mathrm{\Phi }}(t,t_0)$ 의 고유값이면, ${\lambda }^{-1},\overline{\lambda },{\overline{\lambda }}^{-1}$ 도 같은 다중도(multiplicity)를 갖는 고유값이 된다.

이제 시스템 (2)의 상태천이행렬을 구하기 위하여 식 (18)을 이용하기로 한다. 상태변수 $\delta \mathbf{z}$ 와 $\delta \mathbf{x}$ 의 좌표변환 행렬 $Q$ 는 식 (11)과 (12)에 의해서 다음과 같이 구할 수 있다.

 

$$\begin{array}{}\text{(22)}& \delta \mathbf{z}=Q\delta \mathbf{x},Q=\left[\begin{array}{cc}I& 0\\ K& I\end{array}\right],K=\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right]\end{array}$$

 

식 (22)를 식 (18)에 대입하면 다음과 같이 된다.

 

$$\begin{array}{}\text{(23)}& \delta \mathbf{x}(t)=Q^{-1}\tilde{\mathrm{\Phi }}(t,t_0)Q\delta \mathbf{x}(t_0)\end{array}$$

 

위 식을 식 (8)과 비교하면 시스템 (2)의 상태천이행렬 $\mathrm{\Phi }(t,t_0)$ 를 다음과 같이 계산할 수 있다.

 

$$\begin{array}{}\text{(24)}& \mathrm{\Phi }(t,t_0)=Q^{-1}\tilde{\mathrm{\Phi }}(t,t_0)Q\end{array}$$

 

위 식에 의하면 $\mathrm{\Phi }(t,t_0)$ 와 $\tilde{\mathrm{\Phi }}(t,t_0)$ 는 서로 상사(similarity)관계에 있으므로 고유값은 서로 같다. 그리고 행렬식도 $det\mathrm{\Phi }(t,t_0)=det\tilde{\mathrm{\Phi }}(t,t_0)=1$ 이다.

식 (24)를 (21)에 대입하면,

 

$$\begin{array}{r}\text{(25)}& & {\mathrm{\Phi }}^T(t,t_0)Q^{T}JQ\mathrm{\Phi }(t,t_0)=Q^{T}JQ\\ & Q^{T}JQ=\left[\begin{array}{cc}2K& I\\ -I& 0\end{array}\right]\end{array}$$

 

이 되어서 $\mathrm{\Phi }(t,t_0)$ 는 $Q^{T}JQ$ 에 대한 심플렉틱 행렬이 된다.

시스템 (2)의 모노드로미 행렬은 식 (6)에 의하면 다음과 같다.

 

$$\begin{array}{}\text{(26)}& M=\mathrm{\Phi }(t_0+T,t_0)\end{array}$$

 

따라서 모노드로미 행렬은 행렬식이 항상 $1$ 이며 $\mu$ 가 $M$ 의 고유값이면, ${\mu }^{-1},\overline{\mu },{\overline{\mu }}^{-1}$ 도 같은 다중도를 갖는 고유값이 된다.

만약 주기궤도의 섭동 $\delta \mathbf{x}(t)$도 주기가 $T$ 인 주기함수라면 식 (8)에 의해서

 

$$\begin{array}{r}\text{(27)}& \delta \mathbf{x}(t_0+T)=\delta \mathbf{x}(t_0)& =\mathrm{\Phi }(t_0+T,t_0)\delta \mathbf{x}(t_0)\\ & =M\delta \mathbf{x}(t_0)\end{array}$$

 

이 되므로 $M$ 은 고유값 $1$ 을 가지며 그에 해당하는 고유벡터는 $\delta \mathbf{x}(t_0)$ 이다. $M\in {\mathbb{R}}^{6\times 6}$ 이므로 $M$ 의 고유값은 중복된 값을 포함 $6$ 개가 있으며 행렬식이 $1$ 이므로 고유값을 모두 곱하면 $1$ 이다. 여기서 증명하지는 않겠지만 모노드로미 행렬의 $6$ 개의 고유값 중 $2$ 개는 항상 $1$ 이 된다. 따라서 각 고유값은 다음과 같이 주어진다.

 

$$\begin{array}{r}\text{(28)}& & {\mu }_1={\mu }_2=1\\ & {\mu }_3{\mu }_4=1,{\mu }_5{\mu }_6=1\end{array}$$

 

주기궤도의 안정성은 ${\mu }_3,{\mu }_4,{\mu }_5,{\mu }_6$ 에 의해서 결정된다. 고유값은 서로 역수의 관계에 있으므로 한 고유값이 안정하다면 다른 고유값은 불안정하다. 하지만 모든 고유값이 단위 원(unit circle)상에 있는 결레복소수라면 궤도는 안정하다.

 

 

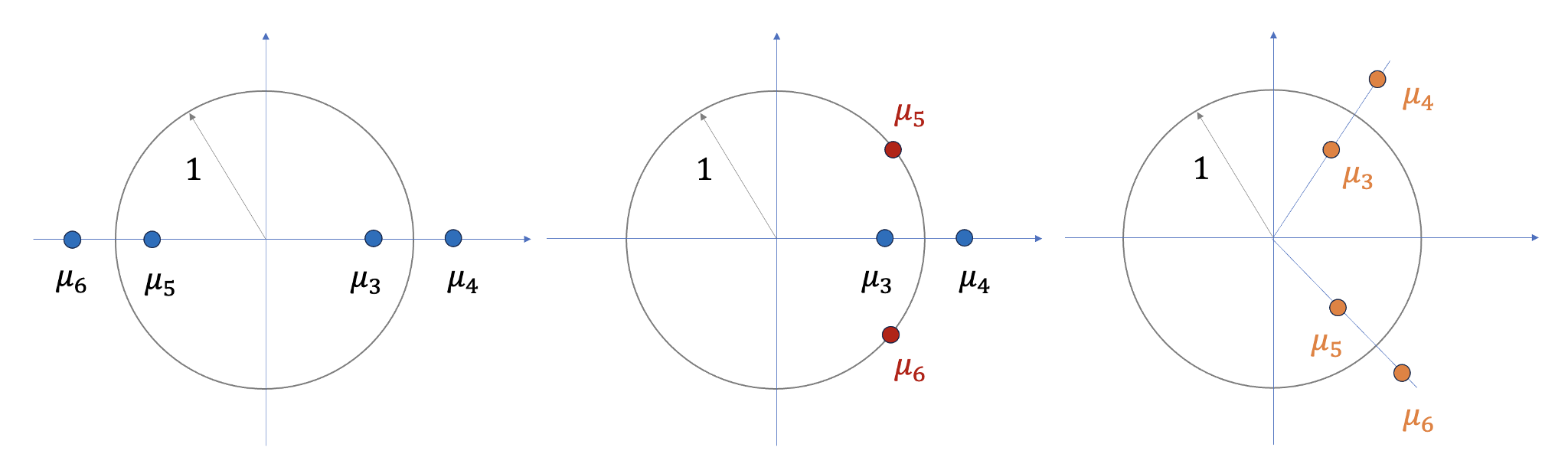
모노드로미 행렬 $M$ 은 주기궤도를 따라 상태천이행렬 $\mathrm{\Phi }(t_0+t,t_0)$ 를 시간 $t_0$ 에서 $t_0+T$ 까지 수치적분하여 얻을 수 있다. 행렬이 얻어지면 고유값을 수치적으로 계산할 수 있다.

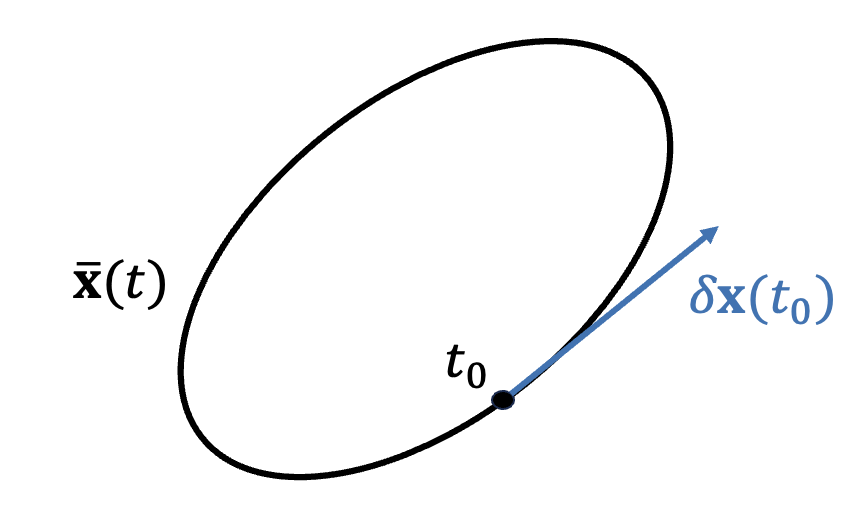
한편 식 (1)을 시간 미분하면 다음과 같다.

 

$$\begin{array}{}\text{(29)}& \frac{d\dot{\overline{\mathbf{x}}}(t)}{dt}=\frac{\partial \mathbf{f}(\overline{\mathbf{x}}(t))}{\partial \overline{\mathbf{x}}(t)}\dot{\overline{\mathbf{x}}}(t)=A(t)\dot{\overline{\mathbf{x}}}(t)\end{array}$$

 

식 (29)와 (2)에 의해서 만약 $\delta \mathbf{x}(t)$ 가 주기함수라면,

 

$$\begin{array}{}\text{(30)}& \delta \mathbf{x}(t)=\dot{\overline{\mathbf{x}}}(t)=\mathbf{f}(\overline{\mathbf{x}}(t))\end{array}$$

 

이이 성립한다. 따라서 $M$ 이 고유값 ${\mu }_1=1$ 을 가질 때의 고유벡터는 $\delta \mathbf{x}(t_0)$ 는 $\delta \mathbf{x}(t_0)=\dot{\overline{\mathbf{x}}}(t_0)$ 로서 주기궤도의 접선 방향이다.