[CR3BP] 리야프노프 궤도 (Lyapunov Orbit) 계산

리야프노프 궤도(Lyapunov orbit)는 (x-y) 평면에서 라그랑지 포인트 L1, L2, L3를 중심으로 공전하는 주기궤도(periodic orbit)이다. 앞서 살펴본 주기궤도의 조건 (https://pasus.tistory.com/277)에 따라 리야프노프 궤도는 x축에 대해 대칭이고, x축을 직각으로 통과한다.

따라서 시간 $t_0$ 의 초기조건과 주기 $T$ 의 반인 시간 $T/2$ 에서의 상태벡터는 다음과 같아야 한다.

 

$$\begin{array}{}\text{(1)}& \mathbf{x}(t_0)=\left[\begin{array}{c}x(t_0)\\ y(t_0)\\ \dot{x}(t_0)\\ \dot{y}(t_0)\end{array}\right]=\left[\begin{array}{c}{x}_0\\ 0\\ 0\\ v_{y0}\end{array}\right],\mathbf{x}(T/2)=\left[\begin{array}{c}x(T/2)\\ 0\\ 0\\ v_y(T/2)\end{array}\right]\end{array}$$

 

리야프노프 궤도를 구하기 위해서는 반주기($T/2$) 시간에서 x축을 직각으로 통과하도록 초기조건 $(x_0,v_{y0})$ 을 잘 선정하는 것이 핵심이다.

 

 

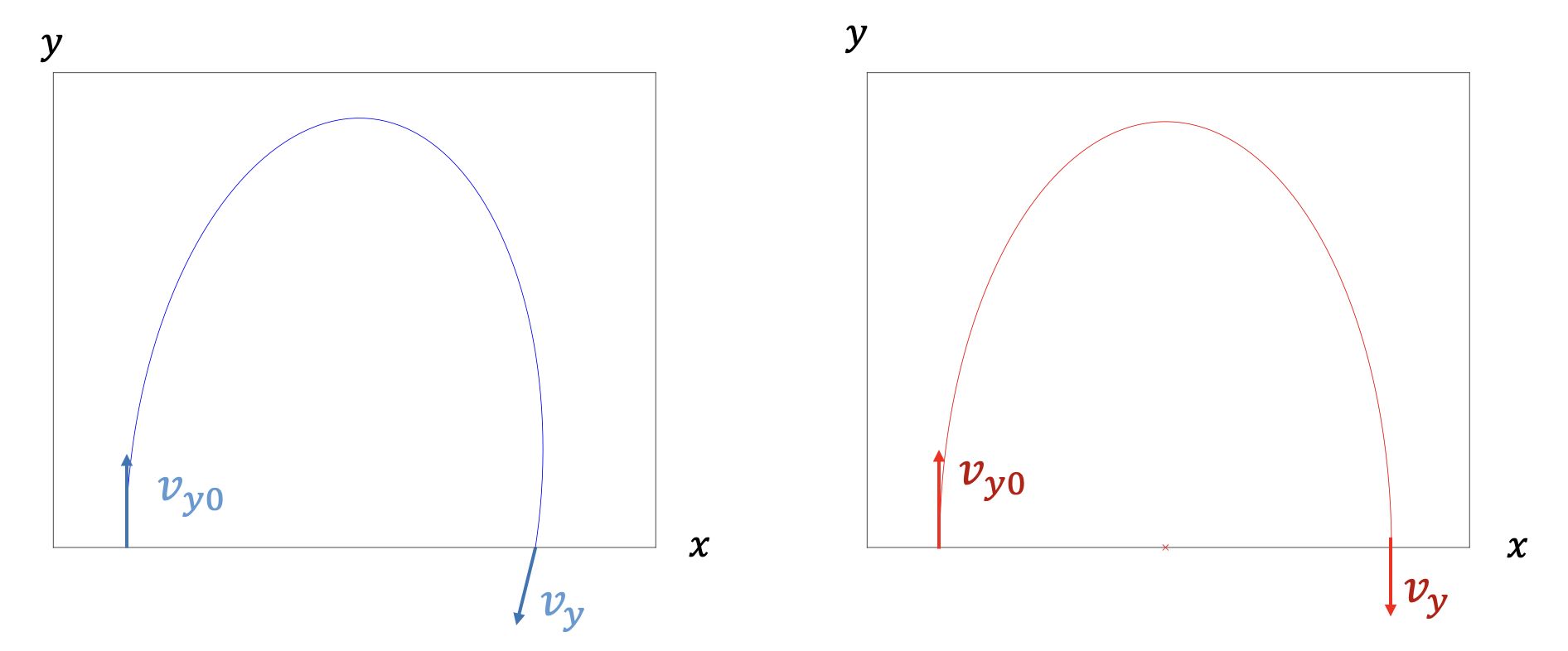
리야프노프 궤도의 계산 절차는 다음과 같다.

 

 

1. 선형화 운동모델의 주기궤도로부터 초기조건의 추측값(initial guess)을 계산한다 (https://pasus.tistory.com/273).

 

$$\begin{array}{}\text{(2)}& \mathbf{x}(t_0)=\left[\begin{array}{c}x(t_0)\\ y(t_0)\\ \dot{x}(t_0)\\ \dot{y}(t_0)\end{array}\right]=\left[\begin{array}{c}{x}_e-A_x\\ 0\\ 0\\ {\omega }_p\kappa A_x\end{array}\right]\end{array}$$

 

여기서 $x_e$ 는 라그랑지 포인트 L1, L2, L3의 위치이고 $A_x>0$ 은 궤도의 x 축 반경이며

 

$$\begin{array}{r}\text{(3)}& \kappa & =\frac{{\omega }_p^2+(1+2c_2)}{2{\omega }_p}\\ c_2& =\frac{(1-\mu )}{|x_e+\mu {|}^3}+\frac{\mu }{|x_e+\mu -1{|}^3}\\ \\ {\omega }_p^2& =\frac{2-c_2+\sqrt{9c_2^2-8c_2}}{2}\end{array}$$

 

이다. 이에 해당하는 매트랩 코드는 다음과 같다.

 

% cr3bp linear dynamics for Lypapunov orbit
% input:
%       Lpoint: Lagrange point 1 or 2 (not 3)
%       Ax: x-axis amplitude
%       param
% output:
%       x0: initial x-position
%       vy0: initial y_dot
%       wp: frequency
%       kappa: Ay = kappa*Ax
%
% coded by st.watermelon

% unpack
mu = param.mu;
if Lpoint == 1
    xe = param.L1; % x-position of Lagrange point
else
    xe = param.L2;
end


% parameter computation
c2 = (1-mu)/(sqrt((xe+mu)^2))^3 + mu/(sqrt((xe+mu-1)^2))^3;
wp2 = 1/2 * (2 - c2 + sqrt(9*c2*c2-8*c2));
wp = sqrt(wp2);
kappa = (wp2+1+2*c2)/(2*wp);

% initial guess
x0 = xe - Ax;
vy0 = wp*kappa*Ax;

 

2. 초기조건의 추측값 식 (2)를 이용하여 CR3BP의 무차원 비선형 운동방정식을 $y=0$ 이 될 때까지 수치적분한다. $y=0$ 일 때의 시간을 $t_1$ 으로 표기한다.

 

$$\begin{array}{r}\text{(4)}& \dot{\mathbf{x}}(t)& =\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ {\dot{v}}_x\\ {\dot{v}}_y\end{array}\right]=\mathbf{f}(\mathbf{x}(t))\\ & =\left[\begin{array}{c}{v}_x\\ v_y\\ 2v_y+x-\frac{(1-\mu )(x+\mu )}{r_1^3}-\frac{\mu (x+\mu -1)}{r_2^3}\\ -2v_x+y-\frac{(1-\mu )y}{r_1^3}-\frac{\mu y}{r_2^3}\end{array}\right]\end{array}$$

 

여기서

 

$$\begin{array}{rl}& r_1=\sqrt{(x+\mu {)}^2+y^2}\\ \\ & r_2=\sqrt{(x+\mu -1{)}^2+y^2}\end{array}$$

 

이다. CR3BP 비선형 운동방정식의 매트랩 코드는 다음과 같다.

 

function X_dot = cr3bp_ode_2d(t, X, mu)
% CR3BP nonlinear differential equation 2D version
% input:
%       t
%       X: [x, y, vx, vy]
%       mu
% output:
%       X_dot
%
% coded by st.watermelon

X_dot = zeros(4,1);

% unpack
x = X(1);
y = X(2);
vx = X(3);
vy = X(4);

% paramter computation
r1 = sqrt((x+mu)^2 + y^2);
r2 = sqrt((x+mu-1)^2 + y^2);

% xvec_dot computation
X_dot(1) = vx;
X_dot(2) = vy;
X_dot(3) = 2*vy + x - (1-mu)*(x+mu)/r1^3 - mu*(x+mu-1)/r2^3;
X_dot(4) = -2*vx + y - (1-mu)*y/r1^3 - mu*y/r2^3;

 

3. 시간 $t_1$ 에서 $v_x=0$ 인지 확인한다. 아니라면 y축 초기속도 $v_{y0}$ 를 조정하기 위한 미분보정(differential correction)을 실시해야 한다. 미분보정을 위해서 다음과 같이 상태천이행렬 미분방정식을 만든다 (https://pasus.tistory.com/274).

 

$$\begin{array}{}\text{(5)}& \frac{d}{dt}\mathrm{\Phi }(t,t_0)=A(t)\mathrm{\Phi }(t,t_0),\mathrm{\Phi }(t_0,t_0)=I\end{array}$$

 

여기서 $A(t)$ 는 식 (4)를 수치적분한 궤적 $\mathbf{x}(t)$ 에서 선형화한 미분방정식의 시스템 행렬로서

 

$$\begin{array}{}\text{(6)}& A(t)={\frac{\partial \mathbf{f}}{\partial \mathbf{x}}|}_{\mathbf{x}(t)}={\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ -{\overline{U}}_{xx}(t)& -{\overline{U}}_{xy}(t)& 0& 2\\ -{\overline{U}}_{xy}(t)& -{\overline{U}}_{yy}(t)& -2& 0\end{array}\right]}_{\mathbf{x}(t)}\end{array}$$

 

이며, 각 성분은 다음과 같이 계산된다.

 

$$\begin{array}{rl}\text{(7)}& & {\overline{U}}_{xx}(t)=-1-\frac{3(1-\mu )(x+\mu {)}^2}{r_1^5}-\frac{3\mu (x+\mu -1{)}^2}{r_2^5}& +\frac{(1-\mu )}{r_1^3}+\frac{\mu }{r_2^3}\\ \\ & {\overline{U}}_{yy}(t)=-1-\frac{3(1-\mu )y^2}{r_1^5}-\frac{3\mu y^2}{r_2^5}+\frac{(1-\mu )}{r_1^3}+\frac{\mu }{r_2^3}\\ \\ & {\overline{U}}_{xy}(t)=-\frac{3(1-\mu )(x+\mu )y}{r_1^5}-\frac{3\mu (x+\mu -1)y}{r_2^5}\end{array}$$

 

식 (5)의 미분방정식을 시간 $t_1$ 까지 수치적분하여 $\mathrm{\Phi }(t_1,t_0)$ 을 계산한다. 상태천이행렬 $\mathrm{\Phi }(t,t_0)$ 는 $4\times 4$ 행렬이므로 $16$ 개의 스칼라 미분방정식이 나오고 식 (4) 또한 $4$ 개의 스칼라 미분방정식이므로 $\mathrm{\Phi }(t_1,t_0)$ 을 계산하기 위해서는 총 $20$ 개의 미분방정식을 수치적분해야 한다. 이에 대한 해당하는 매트랩 코드는 다음과 같다.

 

function Phi_dot = state_trans_ode_2d(t, Phi, mu)
%
% CR3BP state transition matrix differential equation 2D version
% input:
%       t
%       Phi: 16x1 for state transition matrix
%             4x1 for cr3bp state
%       mu
% output
%       Phi_dot: 16x1 for state transition matrix dot
%                 4x1 for cr3bp state
%
% coded by st.watermelon

Phi_dot = zeros(20,1);

% unpack
x = Phi(17);
y = Phi(18);
vx = Phi(19);
vy = Phi(20);

% parameter computation
r1 = sqrt((x+mu)^2 + y^2);
r2 = sqrt((x+mu-1)^2 + y^2);

Uxx = -1 - 3*(1-mu)*(x+mu)^2/r1^5 - 3*mu*(x+mu-1)^2/r2^5 + (1-mu)/r1^3 + mu/r2^3;
Uyy = -1 - 3*(1-mu)*y^2/r1^5 - 3*mu*y^2/r2^5 + (1-mu)/r1^3 + mu/r2^3;
Uxy = -3*(1-mu)*(x+mu)*y/r1^5 - 3*mu*(x+mu-1)*y/r2^5;

% Phi_dot computation
A = [0     0     1  0;
     0     0     0  1;
    -Uxx  -Uxy   0  2;
    -Uxy  -Uyy  -2  0];

PHI = reshape(Phi(1:16),4,4);
PHI_dot = A * PHI;

Phi_dot(1:16) = reshape(PHI_dot,16,1);
Phi_dot(17) = vx;
Phi_dot(18) = vy;
Phi_dot(19) = 2*vy + x - (1-mu)*(x+mu)/r1^3 - mu*(x+mu-1)/r2^3;
Phi_dot(20) = -2*vx + y - (1-mu)*y/r1^3 - mu*y/r2^3;

 

4. 초기속도 $v_{y}0$ 는 다음 연립방정식을 풀어서 계산할 수 있다.

 

$$\begin{array}{r}\text{(8)}& 0& ={\mathrm{\Phi }}_{24}\delta v_{y0}+v_{y1}\delta t_1\\ \delta v_{x1}& ={\mathrm{\Phi }}_{34}\delta v_{y0}+{\dot{v}}_{x1}\delta t_1\end{array}$$

 

여기서 ${\mathrm{\Phi }}_{ij}$ 는 상태천이행렬 $\mathrm{\Phi }(t_1,t_0)$ 의 성분이다. 식 (8)에서 $v_{y0}$ 를 계산하면 다음과 같다.

 

$$\begin{array}{r}\text{(9)}& \delta v_{y0}& ={({\mathrm{\Phi }}_{34}-\frac{{\dot{v}}_{x1}}{v_{y1}}{\mathrm{\Phi }}_{24})}^{-1}\delta v_{x1}\\ & =-{({\mathrm{\Phi }}_{34}-\frac{{\dot{v}}_{x1}}{v_{y1}}{\mathrm{\Phi }}_{24})}^{-1}{v}_{x1}\end{array}$$

 

식 (9)에서 $v_{y0}$ 를 계산한 후 초기값을 $v_{y0}\leftarrow v_{y0}+\delta v_{y0}$ 로 업데이트한다. 다시 2번항으로 돌아가서 시간 $t_1$ 에서 $v_x=0$ 이 될 때까지 반복하면 리야프노프 궤도가 계산된다.

여기서 $y=0$ 과 $v_x=0$ 의 기준은 $|y|\le {10}^{-11}\sim {10}^{-15},|v_x|\le {10}^{-8}\sim {10}^{-15}$ 일 정도로 매우 정밀하게 계산해야 한다.

 

 

2번항과 4번항에 대한 매트랩 코드는 다음과 같다.

 

function [X0, t1, flag] = dp_cr3bp_2d(X0_guess, mu)
%
% Differential correction for CR3BP 2D version
% input:
%       X0_guess: initial guess from linear dynamics
%               = [x0 0 0 vy0]'
%       mu
% output
%       X0: corrected initial condition
%       t1: corrected half period (T/2)
%
% coded by st.watermelon

% setup
max_iter = 100; % maximum DC iteration
absTol = 1e-15;
relTol = 3e-14;
X0 = X0_guess;

for iter = 1: max_iter
    
    fprintf("iter %2d \n", iter)

    % compute t1 and x, vx, vy, and state transition matrix at y=0
    tspan = [0 10];
    Phi0(1:16) = reshape(eye(4),16,1);
    Phi0(17:20) = X0;

    opt2 = odeset('RelTol',relTol,'AbsTol',absTol,'Events',@events);
    [t, Phi, t1, Phi_t1, ie] = ode113(@(t,Phi) state_trans_ode_2d(t,Phi,mu), tspan, Phi0, opt2);

    t1 = t1(end);
    Phi_t1 = Phi_t1(end,:);

    PHI_t1 = reshape(Phi_t1(1:16), 4,4);
    x1 = Phi_t1(17);
    y1 = Phi_t1(18);
    vx1 = Phi_t1(19);
    vy1 = Phi_t1(20);

    r1 = sqrt((x1+mu)^2 + y1^2);
    r2 = sqrt((x1+mu-1)^2 + y1^2);
    vxdot1 = 2*vy1 + x1 - (1-mu)*(x1+mu)/r1^3 - mu*(x1+mu-1)/r2^3;

    % update initial condition
    dvy0 = -vx1/(PHI_t1(3,4)-PHI_t1(2,4)*vxdot1/vy1);
    
    % learning rate
    eta = 1-0.9^iter;
    X0(4,1) = X0(4,1) + eta*dvy0;

    if abs(vx1) <= 1e-11
        break;
    end

end

if iter == max_iter
    flag = 1;
else
    flag = 0;
end

end % end of function


function [value,isterminal,direction] = events(t,Phi)
%
value = Phi(18); % event y=0
isterminal = 1; % stop integration
direction = -1; % negative direction

 

다음은 선형 방정식으로 계산한 궤도와 비선형 방정식으로 계산한 궤도이다. 궤도의 크기가 커질수록 차이가 발생함을 알 수 있다. 리야프노프 궤도의 크기는 궤도에너지에 따라 달라지며 이에 따라 궤도 주기도 달라지므로 임무 요구조건에 따라 궤도 크기를 설계해야 한다.

 

 

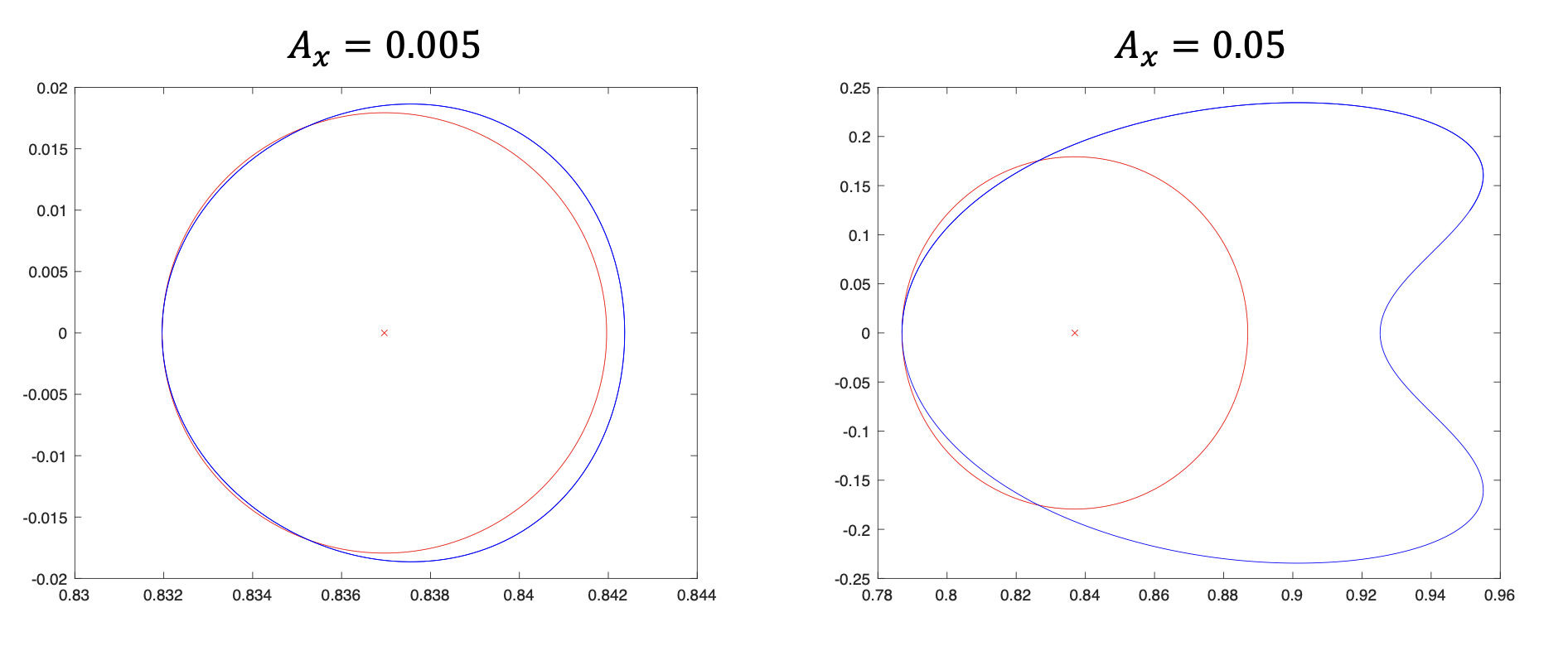
다음은 선형화 방정식으로 리야프노프 궤도의 초기값을 획득한 후, x 좌표값을 $0.001$ 씩 더해 가면서 계산한 지구-달 시스템의 L1과 L2 포인트 리야프노프 궤도들의 집합이다.

 

 

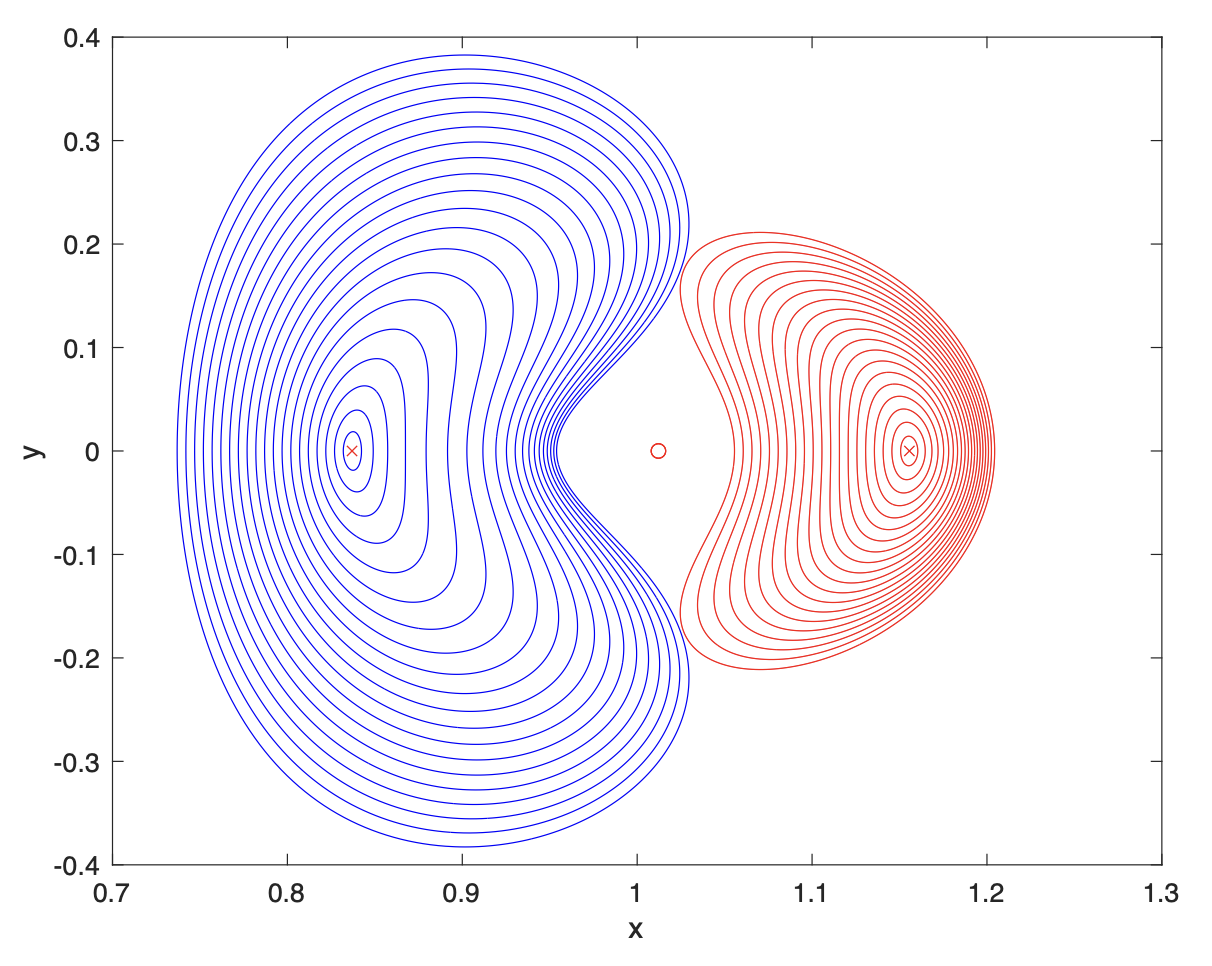
궤도의 크기가 작을 때는 선형화 방정식에서 계산된 궤도의 초기값을 미분보정의 초기 추측값으로 사용해도 잘 수렴하지만 궤도가 커질 수록 초기조건의 추측값에 대해서 미분보정이 매우 민감해 지기 때문에, x 좌표값 $x_0$ 을 서서히 증가시키며 y 축 속도의 초기 추측값으로 전 단계에서 수렴된 궤도의 초기값 $v_{y0}$ 을 사용했다.