오토인코더(AE, autoencoder)는 입력 데이터를 압축하고 의미 있는 표현으로 인코딩한 다음 복원시켜 복원된 데이터가 원본 데이터와 최대한 유사하도록 만든 신경망이다.
AE는 일반적인 용도인 차원축소(dimension reduction) 뿐만 아니라 다양한 응용 분야를 갖고 있는데 그 중 하나가 이상 탐지(anomaly detection) 분야다. 비정상 탐지 또는 이상 탐지란 대부분의 입력 데이터와는 특성이 상이하여 정상이 아닌 것으로 의심을 불러일으킬 만한 어떤 사건 또는 측정값을 식별하는 행위이다. 예를 들면 국내에서 주로 사용되던 신용카드가 갑자기 해외에서 결제된 사건, 공장의 제조라인에서 불량품을 발견하는 일, 또는 센서 또는 시스템의 고장이라고 의심될 만한 측정 신호 검출 등을 들 수 있겠다.
AE를 이용한 이상 탐지 기법은 개념적으로는 간단하다. 만약 정상 데이터로만 AE를 학습하면 원본 데이터와 복원 데이터의 차이인 복원손실 또는 복원오차는 매우 작을 것이다.

하지만 학습된 모델에 학습에 사용한 데이터와 상이한 특성을 갖는 데이터가 입력된다면 이 데이터는 학습되지 않았기 때문에 복원된 데이터는 원본 데이터와 많은 차이가 발생할 것이다. 이 복원오차가 정해진 임계치(threshold)를 넘게 되면 이상으로 판정하는 것이다.

이러한 방법을 시퀀스 또는 시계열(timeseries) 데이터에 적용한 것이 LSTM-AE 이상 탐지 모델이다. LSTM-AE는 인코더와 디코더에 LSTM(Long Short-Term Memory) 신경망을 적용한 오토인코더(AE)다.
최근 각 분야에서 시계열 데이터의 발생 및 수집이 증가함에 따라 시계열 데이터의 이상을 탐지하고자 하는 수요가 증가하고 있다. 시계열 데이터의 이상 상태란 시계열 데이터가 비정상적인 값을 갖는 것으로 의심되는 특정 싯점 또는 일정 구간으로 정의한다.
시계열 데이터를 이용하여 이상 발생 여부를 탐지하는 연구는 오래 전부터 수행되어 왔으나 최근에는 딥러닝 기반의 탐지 모델이 많이 제안되고 있다. 그 중 관심을 모으고 있는 모델 중의 하나가 바로 LSTM-AE이다. 시계열 데이터는 시간적인 특성을 고려해야 하기 때문에 LSTM이 적합하다고 생각하여 AE의 인코더와 디코더에 이 구조를 적용한 것으로 보인다.
LSTM-AE의 작동 방식은 AE와 같다. 우선 LSTM 신경망은 입력 시퀀스를 순차적으로 읽는다. 전체 입력 시퀀스를 모두 읽은 후 고정된 길이를 갖는 벡터로 인코딩한다. 그런 다음 이 벡터를 디코더 LSTM의 입력으로 사용하여 입력 시퀀스를 복원한다. LSTM-AE의 성능은 원본 입력 시퀀스와 복원된 시퀀스간의 차이로 평가된다.

LSTM-AE는 시퀀스 데이터의 특성을 학습할 수 있으며 음성 인식 및 텍스트 번역과 같은 복잡한 시퀀스 예측 문제에서 일정 부분 성과를 냈다. 또한 인코딩된 벡터는 다른 지도학습이나 강화학습 모델, 그리고 물리 시스템의 차원 축소 운동 모델을 구축하는데 사용될 수 있다.
LSTM-AE를 시퀀스 또는 시계열 데이터의 이상 탐지에 적용하기 위해서는 AE 경우와 마찬가지로 정상 시퀀스 데이터로만 학습한다. 학습된 모델에 비정상 시퀀스를 입력하면 높은 복원오차를 보이게 될 것이므로 이 오차가 정해진 임계치를 넘게 되면 이상으로 판정한다.
논문에 의하면 매우 다양한 LSTM-AE 아키텍처와 임계치 설정 방법이 제안되어 있는데, 여기서는 간단한 LSTM-AE 모델을 주식 데이터에 있는 이상 신호 탐지에 적용해 보기로 한다. 사용한 LSTM-AE 구조는 다음과 같다.

인코더는 2층으로 쌓은 LSTM이다. 첫번째 레이어에서는 30개(시퀀스 길이)의 연속한 벡터를 입력으로 받는다. 1층의 은닉 상태변수의 차원은 \(\mathbf{h}_t^{(1)} \in \mathbb{R}^{128}\), 2층의 은닉 상태변수 차원은 \(\mathbf{h}_t^{(2)} \in \mathbb{R}^{64}\), 입력 변수의 차원은 \(\mathbf{x}_t \in \mathbb{R}^1\) 로 설정한다.
이 모델을 코드로 구현하면 다음과 같다.
class Encoder(Model):
def __init__(self, seq_length, latent_dim):
super(Encoder, self).__init__()
self.h1 = LSTM(128, return_sequences=True) # (seq_len, input_dim) -> (seq_len, 128))
self.h2 = LSTM(latent_dim, return_sequences=False) # (seq_len , 128) -> (latent_dim)
self.h3 = RepeatVector(seq_length) # (latent_dim) -> (seq_length, latent_dim)
def call(self, x):
x = self.h1(x)
z = self.h2(x)
z_rep = self.h3(z)
return z, z_rep
Model: "encoder"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
lstm (LSTM) multiple 66560
lstm_1 (LSTM) multiple 49408
repeat_vector (RepeatVector) multiple 0
=================================================================
Total params: 115,968
Trainable params: 115,968
Non-trainable params: 0
1층은 모든 시퀀스에서 은닉 상태를 출력해야 하기 때문에 return_sequences=True 를 사용했지만, 2층은 마지막 시퀀스에서만 출력이 필요하기 때문에 이 속성을 사용하지 않았다. 인코더의 마지막 단계에서 생성된 은닉 상태는 잠재벡터로서 \(\mathbf{z} \in \mathbb{R}^{64}\) 이다. 잠재벡터를 디코더의 첫번째 레이어에 입력으로 사용되기 위해서 RepeatVector 레이어를 통해 30개의 동일한 벡터로 복사한다.
디코더도 2층으로 쌓은 LSTM으로서 인코더의 역순으로 레이어를 구성한다. 첫번째 레이어는 인코더에서 생성한 잠재벡터를 30개(시퀀스 길이)로 복사한 리피트 벡터를 입력으로 받는다. 1층의 은닉 상태변수의 차원은 \(\mathbf{h}_t^{(1)} \in \mathbb{R}^{64}\), 2층의 은닉 상태변수 차원은 \(\mathbf{h}_t^{(2)} \in \mathbb{R}^{128}\) 이다.
class Decoder(Model):
def __init__(self, input_dim, latent_dim):
super(Decoder, self).__init__()
self.h1 = LSTM(latent_dim, return_sequences=True) # (seq_length, latent_dim) -> (seq_len, input_dim)
self.h2 = LSTM(128, return_sequences=True) # (seq_len, input_dim) -> (seq_length, 128)
self.h3 = TimeDistributed(Dense(input_dim)) # (seq_length, 128) -> (seq_length, input_dim)
def call(self, x):
x = self.h1(x)
x = self.h2(x)
x = self.h3(x)
return x
Model: "decoder"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
lstm_2 (LSTM) multiple 33024
lstm_3 (LSTM) multiple 98816
time_distributed (TimeDistr multiple 129
ibuted)
=================================================================
Total params: 131,969
Trainable params: 131,969
Non-trainable params: 0
디코더의 2층 레이어의 출력인 은닉 상태변수에 완전연결(FC) 레이어를 연결하여 1차원의 입력을 복원한다. 이 때 전체 시퀀스에 대해서 동일한 신경망 파라미터를 적용하기 위해서 TimeDistributed 레이어를 사용한다. 그러면 디코더의 출력은 인코더의 입력 시퀀스와 동일한 길이를 갖는 시퀀스가 되며 이를 복원된 시퀀스(constructed sequence)라고 한다. LSTM-AE의 학습 목표는 원본 입력 시퀀스와 복원된 시퀀스간의 차이를 작게 만드는 것이다.
인코더와 디코더를 연결한 LSTM-AE 의 코드는 다음과 같다.
class LstmAE(Model):
def __init__(self, seq_length, input_dim, latent_dim):
super(LstmAE, self).__init__()
self.encoder = Encoder(seq_length, latent_dim)
self.decoder = Decoder(input_dim, latent_dim)
def call(self, x):
z, z_rep = self.encoder(x)
decoded = self.decoder(z_rep)
return decoded
저번 포스트(https://pasus.tistory.com/266)와 마찬가지로 엔비디아 주가 데이터를 이용하여 이상 신호를 탐지해 보도록 하자.
데이터는 지난 5년간의 엔비디아 주식의 종가(close)다. 이 중 2018년5월 29일부터 2022년 6월 30일까지의 종가는 정상적인 데이터로 간주하여 LSTM-AE의 학습에 사용하고, 2022년 7월 1일부터 2023년 5월 26일까지의 데이터는 이상 신호 검출용 데이터로 사용한다. 가만 살펴보니 불과 며칠 사이에 엔비디아 주가가 많이 올라서 신고가를 찍은 듯 하다 (살 걸..).

# split the data into training and testing sets at the mid of 2022
train = data.loc[:'2022-06-30'].copy()
test = data.loc['2022-07-01':].copy()
엔비디아 종가 데이터는 시작일부터 시작하여 하루 씩 이동해 가면서 시퀀스 길이가 30인 데이터로 변환한다.

def to_sequences(x, seq_len=1):
X = []
for i in range(len(x) - seq_len):
X.append(x.iloc[i:(i + seq_len)].values)
return np.array(X)
100번의 에퍽(epoch)을 사용한 학습 결과는 다음과 같다.

파랑색은 LSTM의 학습에 사용된 종가(close) 데이터이고 빨강색은 복원값이다. 복원오차의 히스토그램은 다음과 같다.

오차가 대략 0.08 이하에 몰려 있는 것으로 판단되어 이상 탐지를 위한 임계치(threshold)를 0.08로 설정하고, 2022년 7월 1일 이후의 종가 데이터를 LSTM-AE 모델에 입력해 봤다. 결과는 다음과 같다.
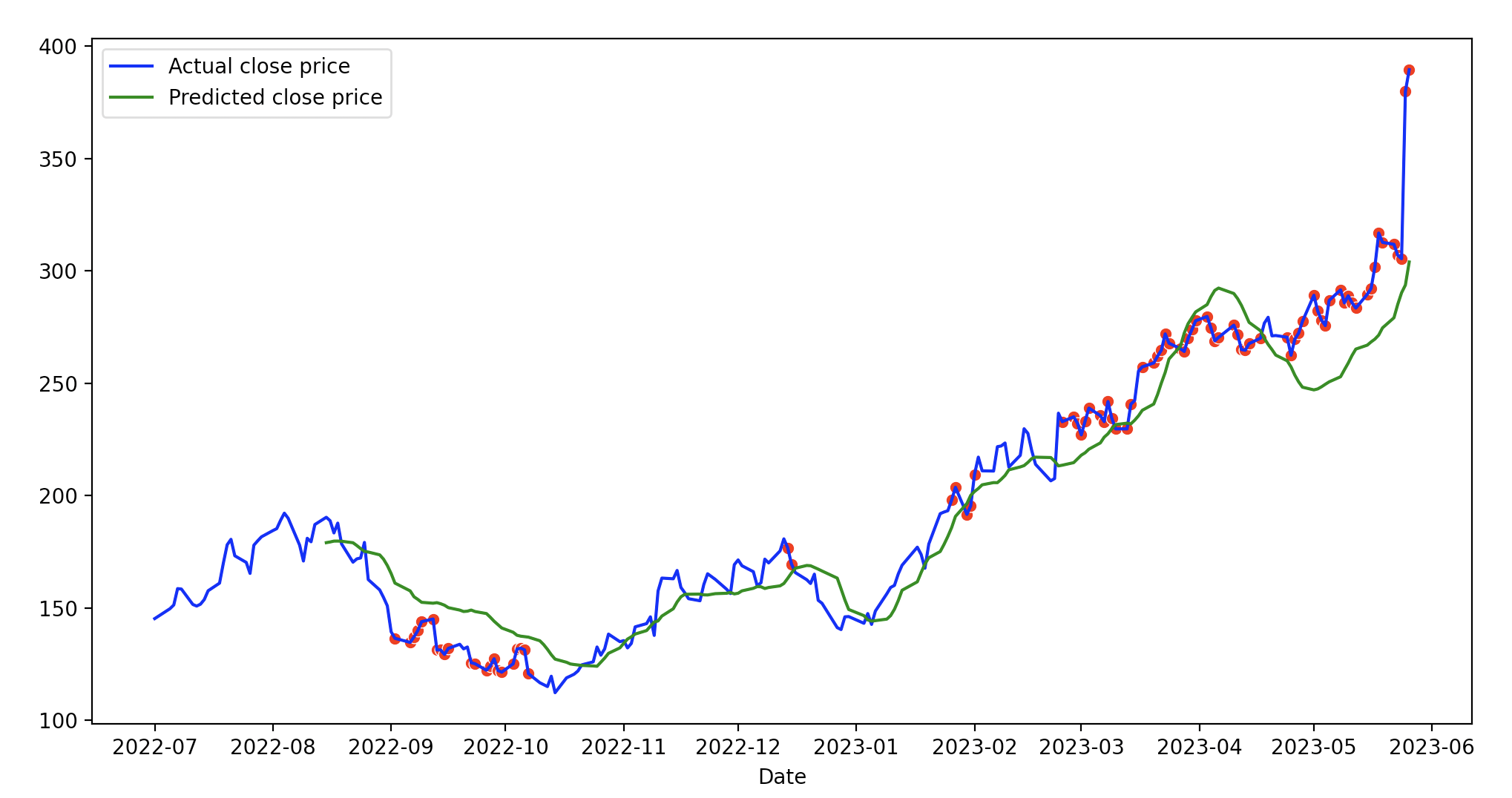
파랑색은 LSTM의 실제 종가(open) 데이터이고 녹색은 복원값이다. 빨강색 점은 이상 신호로 판단한 데이터이다. 제한된 데이터와 임의로 설정한 임계치를 이용한 것이기 때문에 이상 탐지된 부분에 대한 해석은 하지 않겠다.
다음은 Tensorflow 2로 작성한 LSTM-AE 이상 탐지 모델의 전체 코드다.
lstmae_model.py
# LSTM AE model for anomaly detection
# coded by st.watermelon
import numpy as np
from tensorflow.keras.models import Model
from tensorflow.keras.layers import LSTM, Dropout
from tensorflow.keras.layers import RepeatVector, TimeDistributed, Dense
""" LSTM encoder """
class Encoder(Model):
def __init__(self, seq_length, latent_dim):
super(Encoder, self).__init__()
self.h1 = LSTM(128, return_sequences=True) # (seq_len, input_dim) -> (seq_len, 128))
self.h2 = LSTM(latent_dim, return_sequences=False) # (seq_len , 128) -> (latent_dim)
self.h3 = RepeatVector(seq_length) # (latent_dim) -> (seq_length, latent_dim)
def call(self, x):
x = self.h1(x)
z = self.h2(x)
z_rep = self.h3(z)
return z, z_rep
""" LSTM dncoder """
class Decoder(Model):
def __init__(self, input_dim, latent_dim):
super(Decoder, self).__init__()
self.h1 = LSTM(latent_dim, return_sequences=True) # (seq_length, latent_dim) -> (seq_len, input_dim)
self.h2 = LSTM(128, return_sequences=True) # (seq_len, input_dim) -> (seq_length, 128)
self.h3 = TimeDistributed(Dense(input_dim)) # (seq_length, 128) -> (seq_length, input_dim)
def call(self, x):
x = self.h1(x)
x = self.h2(x)
x = self.h3(x)
return x
""" LSTM AE """
class LstmAE(Model):
def __init__(self, seq_length, input_dim, latent_dim):
super(LstmAE, self).__init__()
self.encoder = Encoder(seq_length, latent_dim)
self.decoder = Decoder(input_dim, latent_dim)
def call(self, x):
z, z_rep = self.encoder(x)
decoded = self.decoder(z_rep)
return decoded
lstmae_train.py
# LSTM AE model train for anomaly detection
# coded by st.watermelon
import os
import numpy as np
import pandas as pd
from tensorflow.keras.optimizers import Adam
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import seaborn as sns
from lstmae_model import LstmAE
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "2"
config ={}
config['seq_len'] = 30
config['latent_dim'] = 64
""" loading training and test stock data """
def get_stock_data(grimOn=1):
stock_data = pd.read_csv('data/NVDA.csv')
data = stock_data[['Date', 'Close']].copy()
# convert 'Date' column to datetime
data['Date'] = pd.to_datetime(data['Date'])
# set 'Date' as the index of the DataFrame
data.set_index('Date', inplace=True)
if grimOn:
# create figure and axis
fig, ax = plt.subplots()
# use seaborn to plot data
sns.lineplot(x=data.index, y=data['Close'], ax=ax)
# set x-axis major ticks to monthly interval
ax.xaxis.set_major_locator(mdates.MonthLocator())
# format x-tick labels as year and month number
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
# rotate x-tick labels 90 degrees
plt.xticks(rotation=90)
plt.show()
# split the data into training and testing sets at the mid of 2022
train = data.loc[:'2022-06-30'].copy()
test = data.loc['2022-07-01':].copy()
#print(train.tail(5), test.head(5))
#print(data.head(5))
# normalize the dataset
scaler = StandardScaler()
scaler = scaler.fit(train[['Close']])
train.loc[:, 'Close'] = scaler.transform(train[['Close']])
test.loc[:, 'Close'] = scaler.transform(test[['Close']])
data.loc[:, 'Close'] = scaler.transform(data[['Close']])
#print(train.shape, test.shape)
#print(data.shape)
return train, test, scaler, data
""" change stock data to sequential data for LSTM input """
def to_sequences(x, seq_len=1):
X = []
for i in range(len(x) - seq_len):
X.append(x.iloc[i:(i + seq_len)].values)
return np.array(X)
def train():
train, test, scaler, _ = get_stock_data(grimOn=1)
# set sequence length and latent space dimension
seq_len = config['seq_len']
latent_dim = config['latent_dim']
# get train and test data
trainX = to_sequences(train[['Close']], seq_len)
print(trainX[0:5,0, 0], train.head(5))
input_dim = trainX.shape[2]
# specify learning rate
learning_rate = 0.001
# create an Adam optimizer with the specified learning rate
optimizer = Adam(learning_rate=learning_rate)
# create lstm_ae agent
lstm_ae = LstmAE(seq_len, input_dim, latent_dim)
lstm_ae.compile(optimizer=optimizer, loss='mse')
# train
history = lstm_ae.fit(trainX, trainX, epochs=100, batch_size=32, validation_split=0.1, verbose=2)
# save weights
lstm_ae.save_weights("./save_weights/lstm_ae.h5")
# plotting
plt.plot(history.history['loss'], label='Training loss')
plt.plot(history.history['val_loss'], label='Validation loss')
plt.legend()
plt.show()
if __name__ == "__main__":
train()
lstmae_eval.py
# LSTM AE model evaluation for anomaly detection
# coded by st.watermelon
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from lstmae_model import LstmAE
from lstmae_train import config, get_stock_data, to_sequences
def eval(lstm_ae, scaler, train, trainX):
if os.path.exists('./save_weights/lstm_ae.h5'):
lstm_ae.load_weights("./save_weights/lstm_ae.h5")
else:
return 0
# predict on the training data
trainPredict = lstm_ae.predict(trainX)
#print(trainX.shape, trainPredict.shape) # (978,30,1)
# compute mean absolute error
trainMAE = np.mean(np.abs(trainPredict - trainX), axis=1)
#print(trainMAE.shape) # (978,1)
# plot MAE distribution
plt.hist(trainMAE, bins=30)
plt.show()
# assuming the 'Close' price is the first feature
close_feature_index = 0
# select the 'Close' price predictions for the last time step in each sequence
predicted_prices = trainPredict[:, -1, close_feature_index].reshape(-1, 1)
print(predicted_prices.shape, trainPredict.shape) # (978,1) (978,30,1)
# inverse transform the predicted prices
predicted_prices = scaler.inverse_transform(predicted_prices)
# Plot actual vs predicted prices
plt.figure(figsize=(12, 6))
plt.plot(train.index, scaler.inverse_transform(train['Close'].values.reshape(-1, 1)), color='blue',
label='Actual close price')
plt.plot(train.index[len(train.index) - len(predicted_prices):], predicted_prices, color='red',
label='Predicted close price')
plt.legend()
plt.show()
def detect(lstm_ae, seq_len, scaler, max_trainMAE, test, testX):
if os.path.exists('./save_weights/lstm_ae.h5'):
lstm_ae.load_weights("./save_weights/lstm_ae.h5")
else:
return 0
testPredict = lstm_ae.predict(testX)
testMAE = np.mean(np.abs(testPredict - testX), axis=1)
plt.hist(testMAE, bins=30)
plt.show()
# Assuming the 'Close' price is the first feature
close_feature_index = 0
# Select the 'Close' price predictions for the last time step in each sequence
predicted_prices = testPredict[:, -1, close_feature_index].reshape(-1, 1)
# Inverse transform the predicted prices
predicted_prices = scaler.inverse_transform(predicted_prices)
# Plot actual vs predicted prices
plt.figure(figsize=(12, 6))
plt.plot(test.index, scaler.inverse_transform(test['Close'].values.reshape(-1, 1)), color='blue',
label='Actual close price')
plt.plot(test.index[len(test.index) - len(predicted_prices):], predicted_prices, color='green',
label='Predicted close price')
plt.legend()
# Capture all details in a DataFrame for easy plotting
anomaly_df = pd.DataFrame(test[seq_len:])
anomaly_df['testMAE'] = testMAE
anomaly_df['max_trainMAE'] = max_trainMAE
anomaly_df['anomaly'] = anomaly_df['testMAE'] > anomaly_df['max_trainMAE']
anomaly_df['Close'] = test[seq_len:]['Close']
anomalies = anomaly_df.loc[anomaly_df['anomaly'] == True]
# plot anomalies
if not anomalies.empty:
sns.scatterplot(x=anomalies.index,
y=scaler.inverse_transform(anomalies['Close'].values.reshape(-1, 1)).flatten(),
color='r')
#plt.xticks(rotation=90)
plt.show()
if __name__ == "__main__":
seq_len = config['seq_len']
latent_dim = config['latent_dim']
train, test, scaler, data = get_stock_data(grimOn=0)
# get train and test data
trainX = to_sequences(train[['Close']], seq_len)
testX = to_sequences(test[['Close']], seq_len)
dataX = to_sequences(data[['Close']], seq_len)
input_dim = trainX.shape[2]
lstm_ae = LstmAE(seq_len, input_dim, latent_dim)
lstm_ae.build(input_shape=(None, seq_len, input_dim))
ev = 0
if ev == 1:
eval(lstm_ae, scaler, train, trainX)
else:
max_trainMAE = 0.08
detect(lstm_ae, seq_len, scaler, max_trainMAE, test, testX)
'AI 딥러닝 > Sequence' 카테고리의 다른 글
| [seq2seq] 어텐션이 포함된 seq2seq 모델 (0) | 2023.08.23 |
|---|---|
| [seq2seq] 간단한 seq2seq 모델 구현 (0) | 2023.08.17 |
| [LSTM] 주가 예측 (0) | 2023.05.19 |
| [LSTM] TF2에서 단방향 LSTM 모델 구현 - 2 (0) | 2022.07.23 |
| [LSTM] TF2에서 단방향 LSTM 모델 구현 - 1 (0) | 2022.07.21 |




댓글