항공기의 질점 (Point Mass) 운동 모델

전투기 교전 운동 모델, 비행기 성능(performance) 해석 모델, 그리고 단거리 미사일 운동 모델로서 다음과 같이 평평한 지구(flat Earth) 가정 하에서 유도된 질점(point mass) 운동 모델을 많이 사용한다 (https://pasus.tistory.com/181).

 

$$\begin{array}{r}\text{(1)}& & \dot{x}=V\cos \psi \cos \gamma \\ & \dot{y}=V\sin \psi \cos \gamma \\ \\ & \dot{h}=V\sin \gamma \\ \\ & \dot{V}=-\frac{D}{m}+\frac{T\cos ϵ}{m}-g\sin \gamma \\ \\ & \dot{\psi }=\frac{(L+T\sin ϵ)\sin \sigma }{mV\cos \gamma }\\ \\ & \dot{\gamma }=\frac{(L+T\sin ϵ)\cos \sigma }{mV}-\frac{g\cos \gamma }{V}\end{array}$$

 

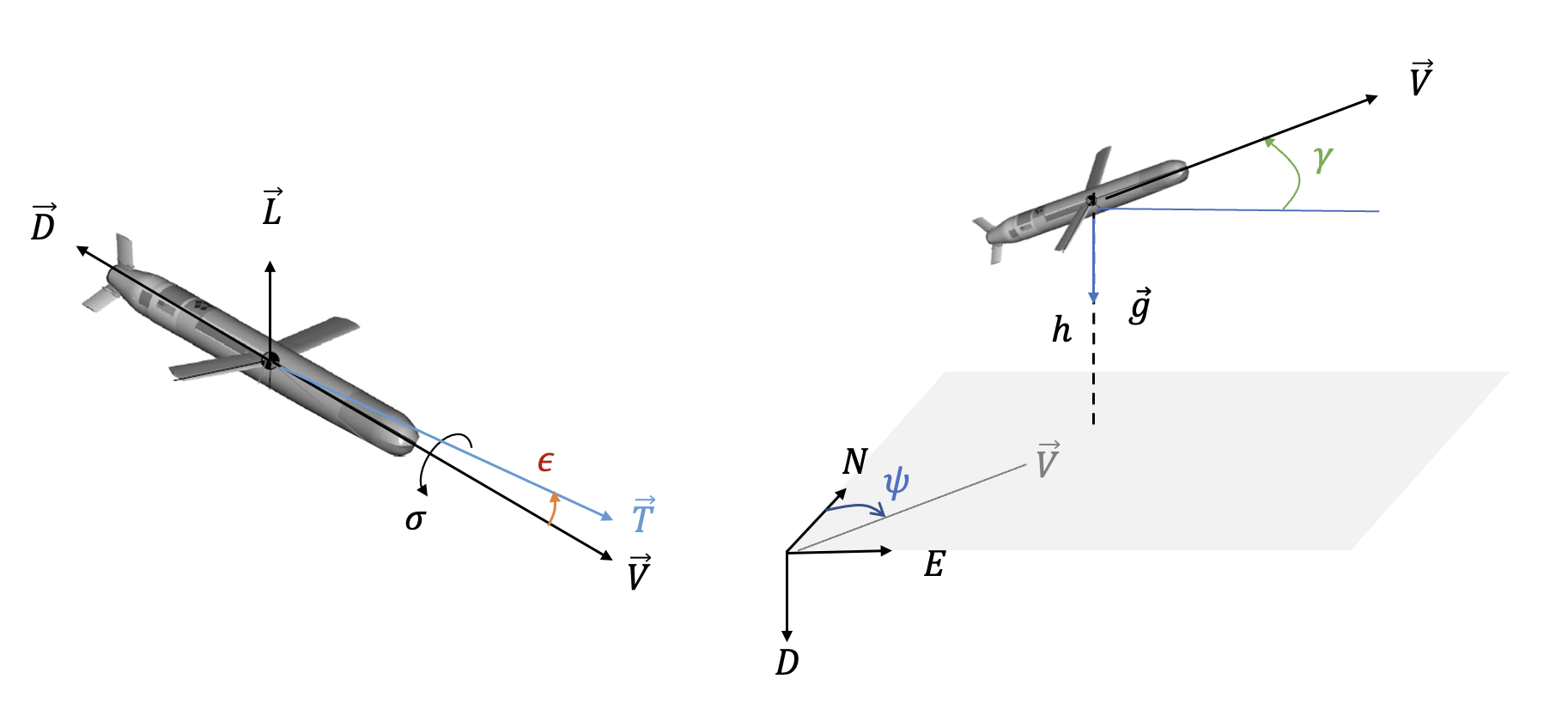
여기서 $\psi$ 는 북쪽 방향에서 동쪽 방향으로 측정한 항공기 속도벡터 $\overrightarrow{V}$ 의 방위각(heading angle), $\gamma$ 는 비행경로각(flight path angle)으로서 수평면과 속도벡터가 이루는 각이다. $\sigma$ 는 속도벡터를 중심으로 회전한 뱅크각(bank angle), $ϵ$ 은 추력벡터 $\overrightarrow{T}$ 와 속도벡터의 사잇각이다. 항공기 센터 라인과 추력벡터가 일치한다고 가정하면 $ϵ$ 은 받음각(angle of attack)으로 해석할 수 있다.

 

 

양력 $L$ 과 항력 $D$ 는 각각 다음과 같이 모델링한다.

 

$$\begin{array}{r}\text{(2)}& & L=\frac{1}{2}\rho V^{2}S{C}_L(\alpha ,Ma)\\ & D=\frac{1}{2}\rho V^{2}S{C}_D(\alpha ,Ma)\end{array}$$

 

여기서 $\rho ,S,C_L,C_D,\alpha ,Ma$ 는 각각 공기 밀도, 기준 면적, 양력계수, 항력계수, 받음각, 마하수(Mach number)이다.

비행기 성능해석에서는 보통 추력벡터와 속도벡터를 같은 방향으로 가정하여 $ϵ=0$ 으로 둔다.

양력이나 항력을 계산하기 위한 공력 모델이 없는 경우에는 다음과 같이 양력과 항공기 무게의 비율인 하중계수(load factor) $n_z$ 와, 이와 유사하게 정의된 전진력(추력-항력) 대 무게 비율인 가속계수 $n_x$ 를 사용하여 식 (1)을 수정한다.

 

$$\begin{array}{r}\text{(3)}& & n_z=\frac{L}{mg}\\ & n_x=\frac{T-D}{mg}\end{array}$$

 

$ϵ=0$ 으로 가정하면 식 (1)은 다음과 같이 된다.

 

$$\begin{array}{r}\text{(4)}& & \dot{x}=V\cos \psi \cos \gamma \\ & \dot{y}=V\sin \psi \cos \gamma \\ \\ & \dot{h}=V\sin \gamma \\ \\ & \dot{V}=g(n_x-\sin \gamma )\\ \\ & \dot{\psi }=\frac{g}{V}\frac{n_z\sin \sigma }{\cos \gamma }\\ \\ & \dot{\gamma }=\frac{g}{V}(n_z\cos \sigma -\cos \gamma )\end{array}$$

 

여기서 $n_x,n_z,\sigma$ 를 직접 제어할 수 있다고 가정하여 제어변수로 사용한다. 식 (4)는 무인 전투기의 교전이나 미사일 회피 기동 제어기 설계를 위한 운동 모델로 많이 사용된다.

전투기 교전 운동 모델에서는 에너지 기동성(energy maneuverability) 분석을 위해서 다음과 같이 항공기 무게 대비 역학 에너지(mechanical energy) $E_s$ 를 운동에너지와 위치에너지의 합으로 정의하고,

 

$$\begin{array}{r}\text{(5)}& E_s& =\frac{\frac{1}{2}m{V}^2+mgh}{mg}\\ & =\frac{V^2}{2g}+h\end{array}$$

 

그 미분 방정식을 식 (1) 또는 (4)의 운동 방정식과 함께 사용하기도 한다.

 

$$\begin{array}{r}\text{(6)}& {\dot{E}}_s& =\frac{V\dot{V}}{g}+\dot{h}\\ & =\frac{(T-D)V}{mg}-V\sin \gamma +V\sin \gamma \\ \\ & =\frac{(T-D)V}{mg}\end{array}$$