상대 궤도요소 (Relative Orbital Elements) - 1

식 (1)로 주어지는 Clohessy-Wiltshire(CW) 방정식

 

$$\begin{array}{r}\text{(1)}& & \ddot{x}-3n^{2}x-2n\dot{y}=0\\ & \ddot{y}+2n\dot{x}=0\\ \\ & \ddot{z}+n^{2}z=0\end{array}$$

 

의 해는 다음과 같았다 (https://pasus.tistory.com/239).

 

 

 

$$\begin{array}{r}\text{(2)}& & x(t)=\frac{{\dot{x}}_0}{n}\sin nt-(3x_0+\frac{2}{n}{\dot{y}}_0)\cos nt+\frac{2}{n}(2n{x}_0+{\dot{y}}_0)\\ & y(t)=2(3x_0+\frac{2}{n}{\dot{y}}_0)\sin nt+\left(\frac{2}{n}{\dot{x}}_0\right)\cos nt+y_0-\frac{2}{n}{\dot{x}}_0-3(2n{x}_0+{\dot{y}}_0)t\\ \\ & z(t)=z_0\cos nt+\frac{{\dot{z}}_0}{n}\sin nt\end{array}$$

 

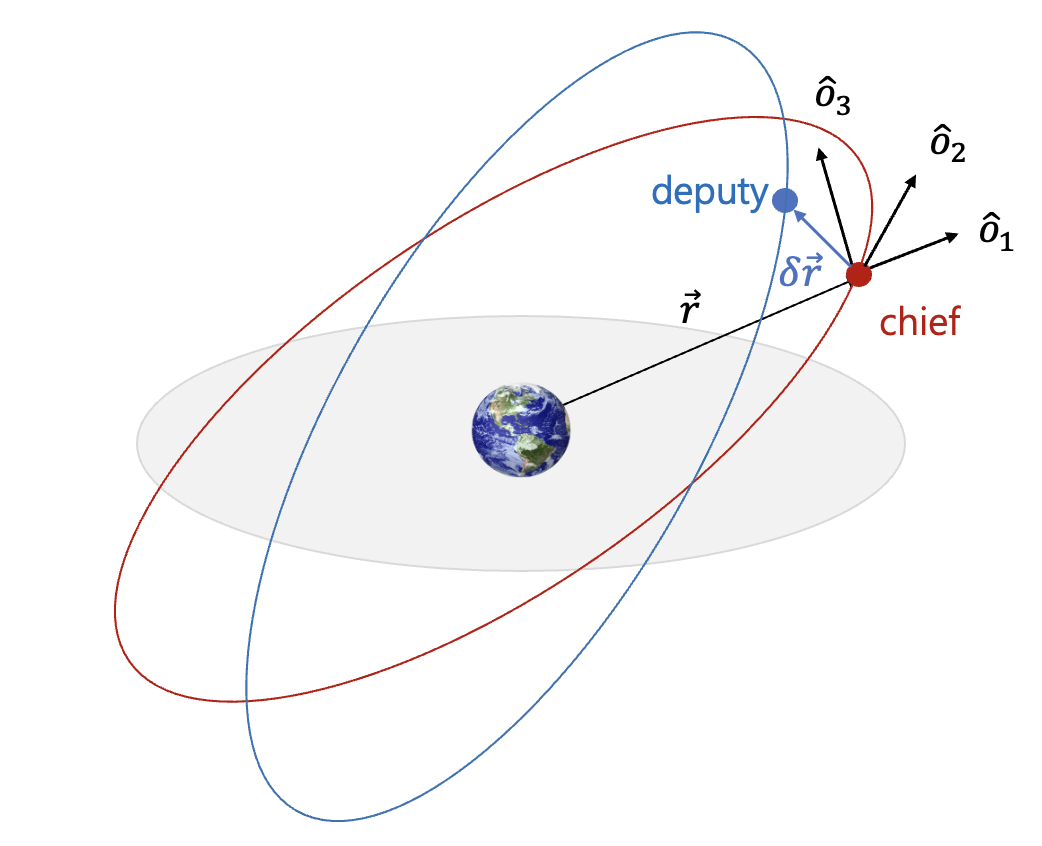
여기서 $x,y,z$ 는 chief 위성에 대한 deputy 위성의 상대 위치를 Hill 좌표계로 표현한 좌표이고 $x_0,y_0,z_0,{\dot{x}}_0,{\dot{y}}_0,{\dot{z}}_0$ 는 각각 $x,y,z$ 와 $\dot{x},\dot{y},\dot{z}$의 초기값이다.

 

 

식 (2)에서 다음과 같이 초기값의 조합으로 이루어진 6개의 상수를 정의하면,

 

$$\begin{array}{r}\text{(3)}& & c_1=4x_0+\frac{2}{n}{\dot{y}}_0\\ & c_2=y_0-\frac{2}{n}{\dot{x}}_0\\ \\ & c_3=3x_0+\frac{2}{n}{\dot{y}}_0\\ \\ & c_4=-\frac{{\dot{x}}_0}{n}\\ \\ & c_5=\frac{{\dot{z}}_0}{n}\\ \\ & c_6=-z_0\end{array}$$

 

CW 방정식의 해는 다음과 같이 쓸 수 있다.

 

$$\begin{array}{r}\text{(4)}& & x(t)=c_1-c_3\cos nt-c_4\sin nt\\ & y(t)=-\frac{3}{2}{c}_{1}nt+c_2+2c_3\sin nt-2c_4\cos nt\\ \\ & z(t)=c_5\sin nt-c_6\cos nt\end{array}$$

 

식 (4)를 위치 $x,y,z$ 뿐만 아니라 속도 $\dot{x},\dot{y},\dot{z}$ 항까지 포함하여 행렬/벡터 형식으로 쓰면 다음과 같다.

 

$$\begin{array}{}\text{(5)}& \left[\begin{array}{c}x(t)\\ y(t)\\ z(t)\\ \dot{x}(t)\\ \dot{y}(t)\\ \dot{z}(t)\end{array}\right]=\left[\begin{array}{cccccc}1& 0& -\cos nt& -\sin nt& 0& 0\\ -\frac{3}{2}nt& 1& 2\sin nt& -2\cos nt& 0& 0\\ 0& 0& 0& 0& \sin nt& -\cos nt\\ 0& 0& n\sin nt& -n\cos nt& 0& 0\\ -\frac{3}{2}n& 0& 2n\cos nt& 2n\sin nt& 0& 0\\ 0& 0& 0& 0& n\cos nt& n\sin nt\end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\\ c_3\\ c_4\\ c_5\\ c_6\end{array}\right]\end{array}$$

 

위 식의 역행렬을 구하면 상수항을 시간 $t$ 에서의 상대 위치와 속도로 표현할 수 있다.

 

$$\begin{array}{}\text{(6)}& \left[\begin{array}{c}{c}_1\\ c_2\\ c_3\\ c_4\\ c_5\\ c_6\end{array}\right]=\left[\begin{array}{cccccc}4& 0& 0& 0& \frac{2}{n}& 0\\ 6nt& 1& 0& -\frac{2}{n}& 3t& 0\\ 3\cos nt& 0& 0& \frac{1}{n}\sin nt& \frac{2}{n}\cos nt& 0\\ 3\sin nt& 0& 0& -\frac{1}{n}\cos nt& \frac{2}{n}\sin nt& 0\\ 0& 0& \sin nt& 0& 0& \frac{1}{n}\cos nt\\ 0& 0& -\cos nt& 0& 0& \frac{1}{n}\sin nt\end{array}\right]\left[\begin{array}{c}x(t)\\ y(t)\\ z(t)\\ \dot{x}(t)\\ \dot{y}(t)\\ \dot{z}(t)\end{array}\right]\end{array}$$

 

식 (5)로 주어지는 CW 방정식의 해는 다음과 같이 진폭/위상 형식으로도 표현할 수 있다.

 

$$\begin{array}{r}\text{(7)}& & x(t)=c_1-c_{34}\cos (nt-\phi )\\ & y(t)=-\frac{3}{2}{c}_{1}nt+c_2+2c_{34}\sin (nt-\phi )\\ \\ & z(t)=c_{56}\sin (nt-\vartheta )\\ \\ & \dot{x}(t)=c_{34}n\sin (nt-\phi )\\ \\ & \dot{y}(t)=-\frac{3}{2}{c}_{1}n+2c_{34}n\cos (nt-\phi )\\ \\ & \dot{z}(t)=c_{56}n\cos (nt-\vartheta )\end{array}$$

 

여기서

 

$$\begin{array}{rl}& c_{34}=\sqrt{c_3^2+c_4^2},\phi ={\tan }^{-1}\left(\frac{c_4}{c_3}\right)\\ \\ & c_{56}=\sqrt{c_5^2+c_6^2},\vartheta ={\tan }^{-1}\left(\frac{c_6}{c_5}\right)\end{array}$$

 

이다. 식 (7)에서 $c_{34}$ 와 $\phi$ 는 Hill 좌표계의 ${\hat{o}}_1$ 축과 ${\hat{o}}_2$ 축에서의 운동에만 관여되므로 chief 위성의 궤도면 내 (in-plane)에서의 상대 운동의 진폭과 위상각이라고 하고, $c_{56}$ 과 $\vartheta$ 는 ${\hat{o}}_3$ 축 운동에만 관여되므로 각각 궤도면 밖 (out-of-plane)으로의 진폭과 위상각이라고 한다.

위 식에서 상수 $c_1,...,c_6$ 는 특정 초기 시간 $t_0$ 에서 상대 위치 벡터와 속도 벡터로 구성된 초기 조건을 사용하여 계산할 수 있지만 실제로는 문제의 물리적 특성에 따라 독립적인 상수로서 주어질 수도 있다.

 

 

한편 이체문제(two-body problem)에서 위성의 궤도는 $6$ 개의 케플러 궤도요소(Kepler orbital elements) 또는 고전 궤도요소 $(a,e,i,\omega ,\mathrm{\Omega },M(\theta ))$ 에 의해서 정의될 수 있다.

 

 

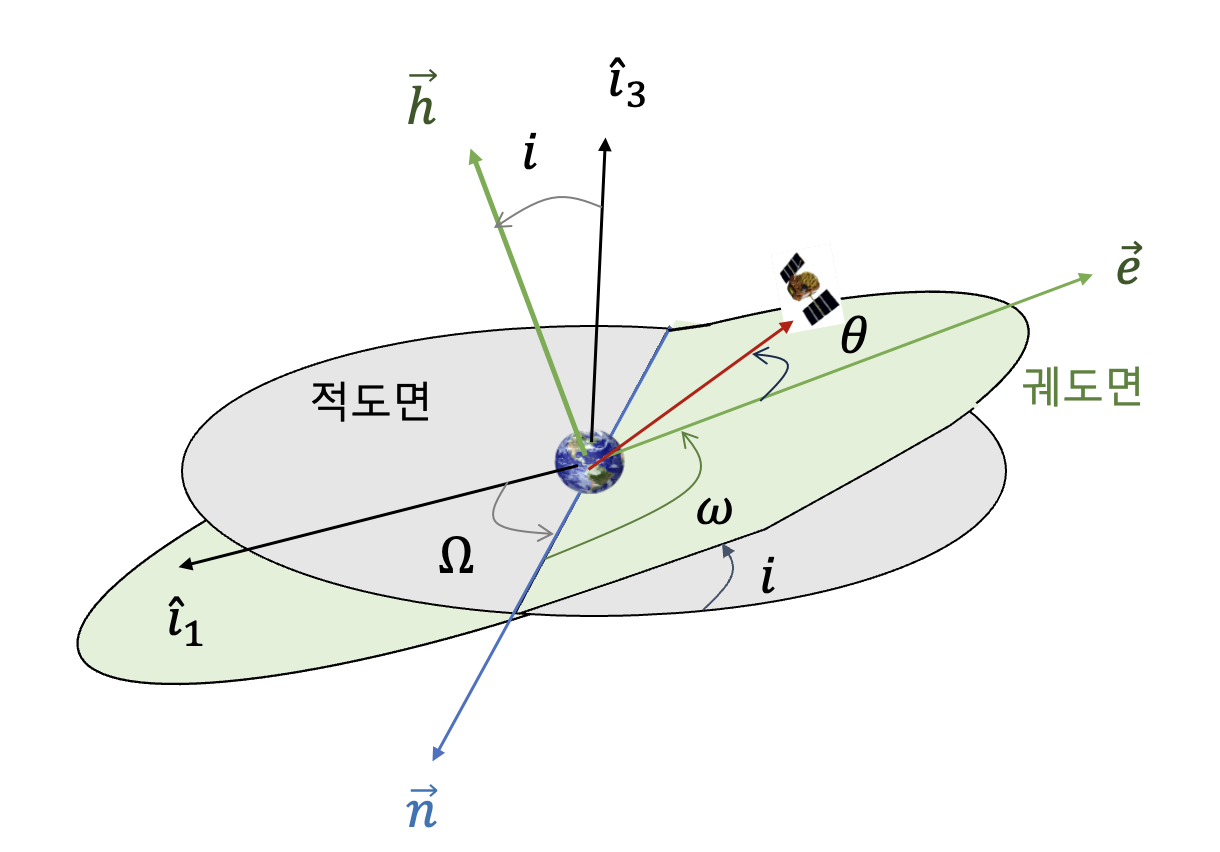
여기서 $a$ 는 장반경(semimajor axis), $e$ 는 이심율(eccentricity), $i$ 는 궤도 경사각(inclination angle), $\omega$ 는 argument of perigee, $\mathrm{\Omega }$ 는 longitude of ascending node, $M$ 은 mean anomaly, $\theta$ 는 true anomaly이다. $(a,e,i,\omega ,\mathrm{\Omega })$ 는 상수이고 $M,\theta$ 는 시간 함수다.

 

$$\begin{array}{}\text{(8)}& \dot{a}=\dot{e}=\dot{i}=\dot{\omega }=\dot{\mathrm{\Omega }}=0,\dot{M}=n=\sqrt{\frac{\mu }{a^3}}\end{array}$$

 

원궤도 또는 적도 궤도인 경우에는 고전 궤도요소 중에서 $\omega ,\mathrm{\Omega }$ 가 정의되지 않기 때문에 수정된 궤도요소를 사용하기도 한다. 원형 비적도 궤도의 경우에는 다음과 같이 준 비특이 궤도요소(quasi-nonsingular orbital elements)를 사용한다.

 

$$\begin{array}{}\text{(9)}& \kappa =\left[\begin{array}{c}a\\ e_x\\ e_y\\ i\\ \mathrm{\Omega }\\ u\end{array}\right]=\left[\begin{array}{c}a\\ e\cos \omega \\ e\sin \omega \\ i\\ \mathrm{\Omega }\\ \omega +M\end{array}\right]\end{array}$$

 

여기서 $(e_x,e_y)$ 를 이심율 벡터 (eccentricity vector) $\overrightarrow{e}$ 의 구성 요소, $u=\omega +M$ 을 mean argument of latitude 라고 한다. 이제 두 위성(chief 와 deputy) 간의 거리 벡터 $\delta \overrightarrow{r}$ 과 궤도요소에 대한 관계식을 알아보도록 한다.

Hill 좌표계에서의 상대 위치 좌표와 두 위성의 고전 궤도요소 사이에는 다음과 같은 근사적인 선형 관계식이 성립한다.

 

$$\begin{array}{r}\text{(10)}& & x(t)\approx \frac{r}{a}\mathrm{\Delta }a+\frac{ae\sin \theta }{\eta }\mathrm{\Delta }M-a\cos \theta \mathrm{\Delta }e\\ & y(t)\approx \frac{r}{{\eta }^3}(1+e\cos \theta {)}^2\mathrm{\Delta }M+r\mathrm{\Delta }\omega \\ & +\frac{r\sin \theta }{{\eta }^2}(2+e\cos \theta )\mathrm{\Delta }e+r\cos i\mathrm{\Delta }\mathrm{\Omega }\\ \\ & z(t)\approx r\sin (\theta +\omega )\mathrm{\Delta }i-r\cos (\theta +\omega )\sin i\mathrm{\Delta }\mathrm{\Omega }\end{array}$$

 

여기서 $(a,e,i,\omega ,\mathrm{\Omega },M(\theta ))$ 는 chief 위성의 궤도요소, $(a_d,e_d,i_d,{\omega }_d,{\mathrm{\Omega }}_d,M_d)$ 는 deputy 위성의 궤도요소이고,

 

$$\begin{array}{rl}& \mathrm{\Delta }a=a_d-a,\mathrm{\Delta }e=e_d-e,\mathrm{\Delta }i=i_d-i,\\ \\ & \mathrm{\Delta }\omega ={\omega }_d-\omega ,\mathrm{\Delta }\mathrm{\Omega }={\mathrm{\Omega }}_d-\mathrm{\Omega },\mathrm{\Delta }M=M_d-M,\\ \\ & \eta =\sqrt{1-e^2}\end{array}$$

 

이다. 두 위성의 이심율 벡터의 차분을 구하면 다음과 같다.

 

$$\begin{array}{r}\text{(11)}& \delta e_x& =e_{x_d}-e_x\\ & \approx (e+\mathrm{\Delta }e)\cos (\omega +\mathrm{\Delta }\omega )-e\cos \omega \\ \\ & \approx \mathrm{\Delta }e\cos \omega -e\mathrm{\Delta }\omega \sin \omega \\ \\ \delta e_y& =e_{y_d}-e_y\\ \\ & \approx (e+\mathrm{\Delta }e)\sin (\omega +\mathrm{\Delta }\omega )-e\sin \omega \\ \\ & \approx e\mathrm{\Delta }\omega \cos \omega +\mathrm{\Delta }e\sin \omega \end{array}$$

 

식 (10)과 (11)은 원형 및 타원형 chief 궤도 모두에 유효하다. 이체문제에서는 mean anomaly $M$ 을 제외하고는 궤도요소가 모두 상수이기 때문에 $\mathrm{\Delta }M$ 을 제외하고는 모든 궤도요소의 차분이 자연스럽게 일정하게 유지된다. 두 궤도 사이에서 $\mathrm{\Delta }a$ 가 $0$ 이 아닌 경우 궤도 주기가 다르기 때문에 두 궤도의 거리는 점차 멀어지게 되는데 식 (10)은 선형화된 식이기 때문에 상대 궤도 사이의 거리 $\delta r$ 이 chief 위성의 궤도 반경 $r$ 에 비해 아주 작을 때만 유효하다는 점에 주의해야 한다.

chief 위성의 이심율이 작다면 $e^2\approx 0$, ${\eta }^2\approx 1$, $r\approx a(1-e\cos \theta )$ 이므로 식 (10)은 다음과 같이 된다.

 

$$\begin{array}{r}\text{(12)}& & x(t)\approx (1-e\cos \theta )\mathrm{\Delta }a+\frac{ae\sin \theta }{\eta }\mathrm{\Delta }M-a\cos \theta \mathrm{\Delta }e\\ & y(t)\approx \frac{a}{\eta }(1+e\cos \theta )\mathrm{\Delta }M+a(1-e\cos \theta )\mathrm{\Delta }\omega \\ & +a\sin \theta (2-e\cos \theta )\mathrm{\Delta }e+a(1-e\cos \theta )\cos i\mathrm{\Delta }\mathrm{\Omega }\\ \\ & z(t)\approx a(1-e\cos \theta )\sin (\theta +\omega )\mathrm{\Delta }i-a(1-e\cos \theta )\cos (\theta +\omega )\sin i\mathrm{\Delta }\mathrm{\Omega }\end{array}$$

 

chief 위성의 궤도가 원궤도 또는 근 원궤도(near-circular orbit)라면 $e\approx 0$, $\eta \approx 1$, $r\approx a$, $\theta \approx M$ 이므로 식 (12)는 다음과 같이 더욱 간략화 된다.

 

$$\begin{array}{r}\text{(13)}& & x(t)\approx \mathrm{\Delta }a-a\cos \theta \mathrm{\Delta }e\\ & y(t)\approx a\mathrm{\Delta }M+a\mathrm{\Delta }\omega +2a\sin \theta \mathrm{\Delta }e+a\cos i\mathrm{\Delta }\mathrm{\Omega }\\ \\ & z(t)\approx a\sin (\theta +\omega )\mathrm{\Delta }i-a\cos (\theta +\omega )\sin i\mathrm{\Delta }\mathrm{\Omega }\end{array}$$

 

상대 이심율 벡터 식 (11)도 다음과 같이 간단해 진다.

 

$$\begin{array}{rl}\text{(14)}& \delta e_x& \approx \mathrm{\Delta }e\cos \omega -e\mathrm{\Delta }\omega \sin \omega & \approx \mathrm{\Delta }e\cos \omega \\ \\ \delta e_y& \approx e\mathrm{\Delta }\omega \cos \omega +\mathrm{\Delta }e\sin \omega \\ & \approx \mathrm{\Delta }e\sin \omega \end{array}$$

 

 

 

식 (14)를 이용하면 식 (13)은 다음과 같이 쓸 수 있다.

 

$$\begin{array}{r}\text{(15)}& \frac{x(t)}{a}& \approx \delta a-\cos (u-\omega )\mathrm{\Delta }e\\ & =\delta a-\mathrm{\Delta }e(\cos u\cos \omega +\sin u\sin \omega )\\ \\ & =\delta a-\delta e_x\cos u-\delta e_y\sin u\\ \\ \frac{y(t)}{a}& \approx \mathrm{\Delta }M+\mathrm{\Delta }\omega +2\sin (u-\omega )\mathrm{\Delta }e+\cos i\mathrm{\Delta }\mathrm{\Omega }\\ \\ & =\delta \lambda +2\mathrm{\Delta }e(\sin u\cos \omega -\cos u\sin \omega )\\ \\ & =\delta \lambda +2\delta e_x\sin u-2\delta e_y\cos u\\ \\ \frac{z(t)}{a}& \approx \sin (M+\omega )\mathrm{\Delta }i-\cos (M+\omega )\sin i\mathrm{\Delta }\mathrm{\Omega }\\ \\ & =\sin u\mathrm{\Delta }i-\cos u\mathrm{\Delta }\mathrm{\Omega }\sin i\\ \\ & =\delta i_x\sin u-\delta i_y\cos u\end{array}$$

 

여기서 $\delta a=\frac{\mathrm{\Delta }a}{a}$, $\delta \lambda$ 는 relative mean longitude, $(\delta i_x,\delta i_y)$ 는 relative inclination vector $\delta \overrightarrow{i}$ 의 구성 요소로서

 

$$\begin{array}{r}\text{(16)}& & \delta \lambda =\mathrm{\Delta }u+\mathrm{\Delta }\mathrm{\Omega }\cos i\\ & \delta i_x=\mathrm{\Delta }i,\delta i_y=\mathrm{\Delta }\mathrm{\Omega }\sin i\end{array}$$

 

이다. 식 (15)에서 $\delta \lambda$ 의 시간 변화율은 다음과 같으므로

 

$$\begin{array}{}\text{(17)}& \delta \dot{\lambda }=\mathrm{\Delta }\dot{u}=-\frac{3}{2}n\delta a\end{array}$$

 

$\delta \lambda$ 는 다음과 같이 쓸 수 있다.

 

$$\begin{array}{}\text{(18)}& \delta \lambda =-\frac{3}{2}nt\delta a+\delta {\lambda }_0\end{array}$$

 

여기서

 

$$\delta {\lambda }_0=\mathrm{\Delta }{u}_0+\mathrm{\Delta }\mathrm{\Omega }\cos i=u_d(0)-u(0)+\mathrm{\Delta }\mathrm{\Omega }\cos i$$

 

이다. 그러면 식 (15)는 다음과 같이 쓸 수 있다.

 

$$\begin{array}{r}\text{(19)}& & \frac{x(t)}{a}\approx \delta a-\delta e_x\cos u-\delta e_y\sin u\\ & \frac{y(t)}{a}\approx -\frac{3}{2}nt\delta a+\delta {\lambda }_0+2\delta e_x\sin u-2\delta e_y\cos u\\ \\ & \frac{z(t)}{a}\approx \delta i_x\sin u-\delta i_y\cos u\end{array}$$

 

식 (19)와 (4)를 비교해 보면

 

$$\begin{array}{r}\text{(20)}& & u=nt,\\ & c_1=a\delta a,c_2=a\delta {\lambda }_0,c_3=a\delta e_x,\\ \\ & c_4=a\delta e_y,c_5=a\delta i_x,c_6=a\delta i_y\end{array}$$

 

일 때 두 식이 완벽히 일치함을 알 수 있다. 그러면 식 (7)에서

 

$$\begin{array}{r}\text{(21)}& & c_{34}=a\sqrt{\delta e_x^2+\delta e_y^2}=a\Vert \delta \overrightarrow{e}{\Vert }_2,\phi ={\tan }^{-1}\left(\frac{\delta e_y}{\delta e_x}\right)\\ & c_{56}=a\sqrt{\delta i_x^2+\delta i_y^2}=a\Vert \delta \overrightarrow{i}{\Vert }_2,\vartheta ={\tan }^{-1}\left(\frac{\delta i_y}{\delta i_x}\right)\end{array}$$

 

로 쓸 수 있다. 따라서 상대 궤도요소(ROE, relative orbital emements)를 다음과 같이 정의한다면,

 

$$\begin{array}{r}\text{(22)}& \delta \kappa & =\left[\begin{array}{c}\delta a\\ \delta {\lambda }_0\\ \delta e_x\\ \delta e_y\\ \delta i_x\\ \delta i_y\end{array}\right]=\left[\begin{array}{c}\delta a\\ \delta {\lambda }_0\\ \Vert \delta \overrightarrow{e}{\Vert }_2\cos \phi \\ \Vert \delta \overrightarrow{e}{\Vert }_2\sin \phi \\ \Vert \delta \overrightarrow{i}{\Vert }_2\cos \vartheta \\ \Vert \delta \overrightarrow{i}{\Vert }_2\sin \vartheta \end{array}\right]\\ & =\left[\begin{array}{c}\frac{a_d-a}{a}\\ (u_d(0)-u(0))+({\mathrm{\Omega }}_d-\mathrm{\Omega })\cos i\\ e_{x_d}-e_x\\ e_{y_d}-e_y\\ i_d-i\\ ({\mathrm{\Omega }}_d-\mathrm{\Omega })\sin i\end{array}\right]\end{array}$$

 

두 위성 간의 상대 좌표를 다음과 같이 ROE의 함수로 표현할 수 있다.

 

$$\begin{array}{rl}\text{(23)}& x& \approx a\delta a-a\delta e_x\cos u-a\delta e_y\sin u& =a\delta a-a\Vert \delta \overrightarrow{e}{\Vert }_2\cos (u-\phi )\\ \\ y& \approx -\frac{3}{2}ua\delta a+a\delta {\lambda }_0+2a\delta e_x\sin u-2a\delta e_y\cos u\\ & =-\frac{3}{2}ua\delta a+a\delta {\lambda }_0+2a\Vert \delta \overrightarrow{e}{\Vert }_2\sin (u-\phi )\\ \\ z& \approx a\delta i_x\sin u-a\delta i_y\cos u\\ & =a\Vert \delta \overrightarrow{i}{\Vert }_2\sin (u-\vartheta )\end{array}$$

 

즉 $n{t}_0=u_0=0$ 에서 mean argument of latitude $u$ 를 독립 변수로 사용하여 Hill 좌표를 일정한 상대 궤도요소의 선형 함수로 표현할 수 있다.

식 (22)로 주어지는 ROE를 준 비특이(quasi-nonsingular) ROE라고 하며 스탠퍼드대 교수 D'Amico가 처음으로 도입하였다.