chief 위성에서 deputy 위성의 까지의 거리가 지구중심에서 chief 위성까지의 거리보다 매우 작은 경우 chief 위성에 대한 deputy 위성의 상대 운동을 Hill 좌표계로 표현하면 다음과 같았다.
\[ \begin{align} & \ddot{x}- \left( \frac{2\mu}{r^3} + \frac{h^2}{r^4} \right) x+ \frac{2(\vec{r} \cdot \vec{v} ) h}{r^4 } y- 2 \frac{h}{r^2 } \dot{y} = f_1 \tag{1} \\ \\ & \ddot{y}+ \left( \frac{\mu}{r^3} - \frac{h^2}{r^4} \right) y - \frac{2(\vec{r} \cdot \vec{v} ) h}{r^4 } x + 2 \frac{h}{r^2 } \dot{x} =f_2 \\ \\ & \ddot{z}+ \frac{\mu}{r^3 } z=f_3 \end{align} \]
여기서 \( \delta \vec{r}=x \hat{o}_1+y\hat{o}_2+z\hat{o}_3\) 는 deputy 위성의 상대 위치 벡터이고 \(\vec{r}\) 과 \(\vec{v}\) 는 chief 위성의 위치벡터와 속도벡터, \(r\) 은 \(\vec{r}\) 의 크기, \(h\) 는 chief 위성의 각운동량 벡터 \(\vec{h}\) 의 크기, \(\mu\) 는 중력 파라미터, \(f_1, f_2, f_3\) 는 섭동력(perturbing specific force)의 차이다.

chief 위성의 궤도를 기준 궤도(reference orbit)이라고 한다. 만약 기준 궤도가 원이라면 위 식은 상당히 단순화된다. 원궤도에서는 \(\vec{r} \cdot \vec{v}=0\) 이고, \(h=\sqrt{\mu r} \) 이므로 식 (1)은 다음과 같이 된다.
\[ \begin{align} & \ddot{x}- \frac{3\mu}{r^3} x - 2 \sqrt{ \frac{\mu}{r^3 }} \dot{y} =f_1 \tag{2} \\ \\ & \ddot{y} + 2 \sqrt{ \frac{\mu}{r^3 }} \dot{x} =f_2 \\ \\ & \ddot{z}+ \frac{\mu}{r^3 } z=f_3 \end{align} \]
또한 원궤도에서 각속력 \(n\) 은 다음과 같이 주어지므로
\[ n= \frac{v}{r} = \frac{ \sqrt{ \frac{\mu}{r}}}{r} = \sqrt{ \frac{\mu}{r^3}} \tag{3} \]
식 (2)는 다음과 같이 된다.
\[ \begin{align} & \ddot{x}- 3n^2 x - 2 n \dot{y} =f_1 \tag{4} \\ \\ & \ddot{y} + 2 n \dot{x} =f_2 \\ \\ & \ddot{z}+ n^2 z=f_3 \end{align} \]
식 (4)를 Clohessy-Wiltshire(CW) 방정식이라고 한다. CW 방정식은 Hill 방정식 또는 Euler-Hill 방정식으로 부르기도 한다. CW 방정식은 1960년대부터 위성 근접 작업, 예를 들면 랑데부나 편대비행 등을 모델링하는데 광범위하게 사용되고 있다. 식 (1)과는 달리 CW 방정식 (4)는 계수가 일정한 시불변(time-invariant) 시스템이기 때문에 섭동력을 무시할 경우(\(f_1=f_2=f_3=0\)) 해석적인 풀이가 가능하다.
섭동력이 모두 \(0\) 이라고 가정하고 CW 방정식 (4)를 풀어보자. \(z\) 방향(cross-track) 상대 운동은 다른 두 방향의 상대 운동과 독립적이고 방정식이 단순하므로 먼저 풀어보도록 한다.
\[ \begin{align} & z(t)=z_0 \cos (nt) + \frac{ \dot{z}_0}{n} \sin (nt) \tag{5} \\ \\ & \dot{z}(t)= -z_0 n \sin (nt) + \dot{z}_0 \cos (nt) \end{align} \]
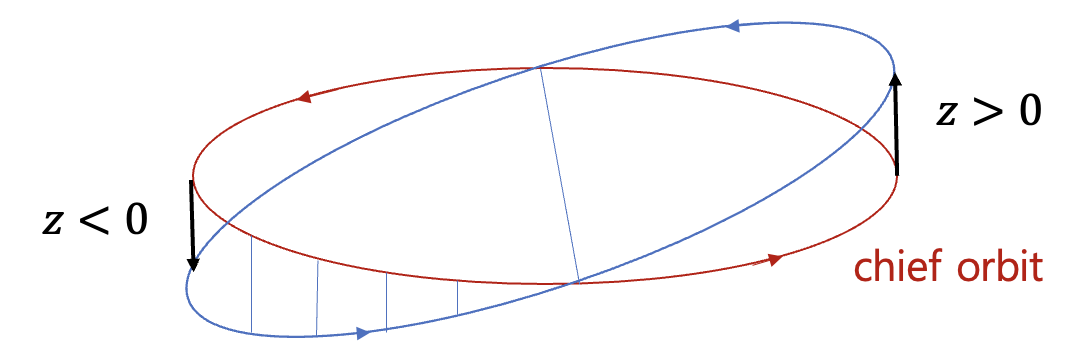
여기서 \(z_0\), \(\dot{z}_0\) 는 각각 \(z\) 와 \(\dot{z}\) 의 초기값이다. \(z\) 방향의 상대 운동은 기준 궤도의 각속력 \(n\) 과 동일한 주파수로 진동한다는 것을 알 수 있다. 물리적으로 이 운동은 기준 궤도와 약간 다른 경사각을 갖는 운동으로 표현할 수 있다.
\(x-y\) (radial/along-track) 운동은 결합되어 있어서 다음과 같이 벡터 행렬식으로 쓸 수 있다.
\[ \begin{bmatrix} \dot{x} \\ \dot{y} \\ \ddot{x} \\ \ddot{y} \end{bmatrix} =\begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 3n^2 & 0 & 0 & 2n \\ 0 & 0 & -2n & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ \dot{x} \\ \dot{y} \end{bmatrix}=A \begin{bmatrix} x \\ y \\ \dot{x} \\ \dot{y} \end{bmatrix} \tag{6} \]
위 식을 풀면 다음과 같다.
\[ \begin{bmatrix} x \\ y \\ \dot{x} \\ \dot{y} \end{bmatrix} =e^{At} \begin{bmatrix} x_0 \\ y_0 \\ \dot{x}_0 \\ \dot{y}_0 \end{bmatrix} = \begin{bmatrix} \Phi_{rr} (t) & \Phi_{rv} (t) \\ \Phi_{vr} (t) & \Phi_{vv} (t) \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \\ \dot{x}_0 \\ \dot{y}_0 \end{bmatrix} \tag{7} \]
여기서 \(x_0\), \(y_0\), \(\dot{x}_0\), \(\dot{y}_0\) 는 각각 \(x, y\) 와 \(\dot{x}, \dot{y}\) 의 초기값이고
\[ \begin{align} & \Phi_{rr} (t)= \begin{bmatrix} 4-3 \cos (nt) & 0 \\ 6(\sin (nt)-nt) & 1 \end{bmatrix} \tag{8} \\ \\ & \Phi_{rv} (t)= \begin{bmatrix} \frac{1}{n} \sin (nt) & \frac{2}{n} (1-\cos (nt) ) \\ \frac{2}{n} (\cos (nt) -1) & \frac{4}{n} \sin (nt)-3t \end{bmatrix} \\ \\ & \Phi_{vr} (t)= \begin{bmatrix} 3n \sin (nt) & 0 \\ 6n (\cos (nt)-1) & 0 \end{bmatrix} \\ \\ & \Phi_{vv} (t)= \begin{bmatrix} \cos (nt) & 2 \sin (nt) \\ -2 \sin (nt) & 4 \cos (nt)-3 \end{bmatrix} \end{align} \]
이다.
\(z\) 방향과 마찬가지로 \(x, y\) 방향 상대 운동도 기준 궤도의 각속력 \(n\) 과 동일한 주파수로 진동한다는 것을 알 수 있다.
식 (7)과 (8)에서 \(x\) 와 \(y\) 를 풀어 쓰면 다음과 같다.
\[ \begin{align} x(t) &= (4-3 \cos (nt) ) x_0+ \frac{1}{n} \sin (nt) \dot{x}_0+ \frac{2}{n} (1-\cos (nt) ) \dot{y}_0 \tag{9} \\ \\ &= \frac{\dot{x}_0}{n} \sin (nt)- \left(3 x_0+ \frac{2}{n} \dot{y}_0 \right) \cos (nt) +4x_0+ \frac{2}{n} \dot{y}_0 \\ \\ y(t) &= 6(\sin (nt)-nt) x_0+y_0+\frac{2}{n} (\cos (nt)-1) \dot{x}_0+ \left( \frac{4}{n} \sin (nt)-3t \right) \dot{y}_0 \tag{10} \\ \\ &= 2 \left( 3x_0+ \frac{2}{n} \dot{y}_0 \right) \sin (nt)+ \left( \frac{2}{n} \dot{x}_0 \right) \cos (nt)+y_0-\frac{2}{n} \dot{x}_0-3(2nx_0+ \dot{y}_0 )t \end{align} \]
식 (10)에 의하면 \(y\) 는 시간이 지남에 따라 선형적으로 증가하는 항을 가지고 있다. 따라서 \(2nx_0+ \dot{y}_0=0\) 이 아닌 이상 deputy 위성은 chief 위성으로부터 멀어질 것이고 둘 사이의 거리는 한없이 증가할 것이다.
식 (6)에서 행렬 \(A\) 의 고유값을 구해보면 다음과 같다.
\[ \begin{align} det(A-sI) &= det \begin{bmatrix} -s & 0 & 1 & 0 \\ 0 & -s & 0 & 1 \\ 3n^2 & 0 & -s & 2n \\ 0 & 0 & -2n & -s \end{bmatrix} \tag{11} \\ \\ &=s^4+n^2 s^2=s^2 (s^2+n^2 )=0 \\ \\ \to & \ s=0, \ 0, \ +jn, \ -jn \end{align} \]
따라서 시스템 (6)은 3개의 운동 모드를 갖는다는 것을 알 수 있다.
먼저 고유값 \(s=0\) 에 해당하는 모드는 일정(constant)한 운동모드라는 것을 짐작할 수 있는데 이 모드만을 발현하기 위한 초기값은 다음과 같다.
\[ x_0=0, \ y_0=arbitrary, \ \dot{x}_0=0, \ \dot{y}_0=0 \tag{12} \]
그러면 식 (9)와 (10)에서
\[ x(t)=0, \ \ y(t)=y_0 \tag{13} \]
가 되므로 deputy 위성은 \(y\) 방향 (along-track) 으로 기준 궤도에 대해 궤도 반지름은 같지만 \(y_0\) 만큼 앞서거나 또는 뒤지는 운동을 하는 것을 알 수 있다.
또 다른 고유값 \(s=0\)(중근)에 해당하는 모드는 일정(constant)한 시간 변화율을 갖는 운동모드라는 것을 짐작할 수 있는데 이 모드만을 발현하기 위한 초기값은 다음과 같다.
\[ x_0=arbitrary,\ y_0=arbitrary, \ \dot{x}_0=0, \ \dot{y}_0= -\frac{3nx_0}{2} \tag{14} \]
그러면 식 (9)와 (10)에서
\[ x(t)=x_0, \ \ y(t)= \frac{-3nx_0}{2} t+y_0 \tag{15} \]
가 되므로 deputy 위성은 기준 궤도에 비해 고도가 높고 (\(x_0 \gt 0\)) 일정 속도로 뒤쳐지는 (\(\dot{y} \lt 0\))운동을 하는 것을 알 수 있다. 반대로 기준 궤도에 비해 고도가 낮으며 (\(x_0 \lt 0\)) 일정 속도로 앞서가는 (\(\dot{y} \gt 0\))운동을 한다.
아래 영상에서 파란색은 deputy 위성, 빨간색은 chief 위성을 나타낸다. 왼쪽 영상은 ECI 좌표계에서, 오른쪽 영상은 Hill 좌표계에서 본 운동이다.
고유값 \(s= \pm jn\) 에 해당하는 모드는 주파수 \(n\) 으로 진동하는 운동모드라는 것을 짐작할 수 있는데 이 모드만을 발현하기 위한 초기값은 다음과 같다.
\[ x_0=arbitrary,\ y_0=arbitrary, \ \dot{x}_0=0, \ \dot{y}_0= -2nx_0 \tag{16} \]
그러면 식 (9)와 (10)에서
\[ x(t)=x_0 \cos (nt), \ \ y(t)= -2x_0 \sin (nt)+y_0 \tag{17} \]
가 되므로 deputy 위성은 chief 위성의 궤도 주기와 같은 주기로 chief 위성 주위를 회전(loop)하는 운동을 하는 것을 알 수 있다.
일반적인 초기값에 대해서는 위 3가지 모드가 복합적으로 나타난다. 초기값에 따라서는 루프 궤적보다는 굽이치는 궤적을 보이기도 한다.
'항공우주 > 우주역학' 카테고리의 다른 글
| 상대 궤도요소 (Relative Orbital Elements) - 2 (0) | 2023.02.07 |
|---|---|
| 상대 궤도요소 (Relative Orbital Elements) - 1 (0) | 2023.02.04 |
| 상대 궤도운동 방정식 (Relative Orbit Equation of Motion) (0) | 2023.01.20 |
| ECEF-LLH 좌표계 상호 변환 매트랩 코드 (1) | 2022.01.01 |
| ECEF 좌표계와 LLH 좌표계 (0) | 2021.12.30 |




댓글