LLH 좌표계에서 ECEF좌표계로 좌표변환하는 문제를 알고리즘 형태로 정리하면 다음과 같다.
입력: 위도 (\(\lambda_{lat}\)), 경도 (\(\lambda_{lon}\)), 높이 (\(h\))
1. 접선반경 (\(R_{tr}\)) 계산: \(R_{tr}=\frac{ R_{eq}}{ \sqrt{1-e_{er}^2 \sin^2 \lambda_{lat}}}\)
2. 벡터 \(r^e\) 계산: \(r^e= \begin{bmatrix} (R_{tr}+h) \cos \lambda_{lat} \cos \lambda_{lon} \\ (R_{tr}+h) \cos \lambda_{lat} \sin \lambda_{lon} \\
\left( R_{tr} (1-e_{er}^2 )+h \right) \sin \lambda_{lat} \end{bmatrix} \)
출력: ECEF좌표계에서의 벡터 (\(r^e\))
위 알고리즘을 매트랩으로 구현하면 다음과 같다.
function R=llh2ecef(lat,lon,h)
% R=llh2ecef(lat,lon,h)
% Converting geodetic data (latitude, longitude, height)
% to position vector R represented in ECEF frame.
% Input: latitude(deg), longitude(deg), height(km)
% Output: position vector R represented in ECEF (km)
% coded by St.Watermelon
Req = 6378.137; % km
e_er = 0.0818191908426;
lat=lat*pi/180;
lon=lon*pi/180;
clat=cos(lat);
slat=sin(lat);
clon=cos(lon);
slon=sin(lon);
Rtr=Req/(sqrt(1-e_er^2*slat^2));
x=(Rtr+h)*clat*clon;
y=(Rtr+h)*clat*slon;
z=(Rtr*(1-e_er^2)+h)*slat;
R=[x y z]';
이번에는 반대로 ECEF좌표계에서 LLH 좌표계로 좌표변환하는 문제를 알고리즘 형태로 정리하면 다음과 같다.
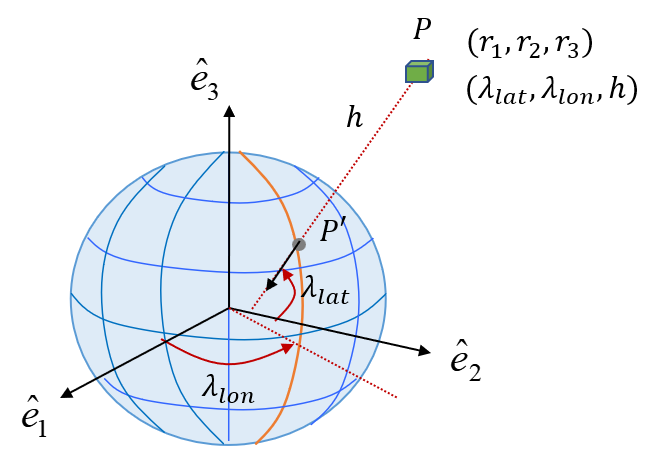
입력: ECEF좌표계에서의 벡터 (\(r^e= \begin{bmatrix} r_1 & r_2 & r_3 \end{bmatrix}^T \))
1. 경도 (\(\lambda_{lon}\)) 계산: \(\lambda_{lon}= \tan^{-1} \left( \frac{r_2}{r_1} \right) \)
2. 위도 (\(\lambda_{lat}\)) 추정
3. 수렴할 때까지 반복계산 (\(h, \lambda_{lat}\))
3-1. 접선반경 (\(R_{tr}\)) 계산: \(R_{tr}=\frac{ R_{eq}}{ \sqrt{1-e_{er}^2 \sin^2 \lambda_{lat}}}\)
3-2. 높이 (\(h\)) 계산: \( h= \frac{ \sqrt{r_1^2+r_2^2}}{\cos \lambda_{lat}} - R_{tr} \)
3-3. 위도 (\(\lambda_{lat}\)) 계산: \( \lambda_{lat} = \tan^{-1} \left( \frac{r_3}{ \sqrt{r_1^2+r_2^2 }} \left( 1- \frac{e_{er}^2 R_{tr}}{R_{tr}+h} \right)^{-1} \right) \)
출력: 위도 (\(\lambda_{lat}\)), 경도 (\(\lambda_{lon}\)), 높이 (\(h\))
위 알고리즘을 매트랩으로 구현하면 다음과 같다.
function [lat,lon,h]=ecef2llh(R)
% [lat,lon,h]=ecef2llh(R)
% Converting position vector R represented in ECEF frame to
% geodetic data (latitude, longitude, height)
%
% Input: position vector R represented in ECEF (km)
% Output: latitude(deg), longitude(deg), height(km)
% coded by St.Watermelon
Req=6378.137; % km
e_er=0.0818191908426;
x=R(1); y=R(2); z=R(3);
lon=atan2(y,x);
h=0; lat=0; % initial guess
going=1;
while going
p=sqrt(x^2+y^2);
Rtr=Req/(sqrt(1-e_er^2*(sin(lat))^2));
h1=p/cos(lat)-Rtr;
tmp=1-e_er^2*Rtr/(Rtr+h1);
lat1=atan(z/(p*tmp));
if (abs(h1-h)<1e-5) & (abs(lat1-lat)<1e-8)
going=0;
else
going=1;
end
h=h1; lat=lat1;
end
lat=lat*180/pi;
lon=lon*180/pi;
'항공우주 > 우주역학' 카테고리의 다른 글
| CW 방정식 (Clohessy-Wiltshire Equations) (0) | 2023.01.27 |
|---|---|
| 상대 궤도운동 방정식 (Relative Orbit Equation of Motion) (0) | 2023.01.20 |
| ECEF 좌표계와 LLH 좌표계 (0) | 2021.12.30 |
| SCI 좌표계와 ECI 좌표계 (0) | 2021.12.30 |
| 기본 궤도 미분 방정식의 무차원화 (0) | 2021.12.30 |




댓글