독립변수가 1개인 함수로 표현되는 신호 \( x[n] \)을 1차원 신호(one-dimensional signal)라고 한다. 여기서 \( n \)은 인덱스로서 정수 값을 갖는다. 이 인덱스는 보통 시간스텝(time step)을 나타낸다. 1차원 신호와 관련된 컨볼루션을 1D 컨볼루션이라고 하거나 그냥 컨볼루션이라고 한다.
독립변수가 2개인 함수로 표현되는 신호 \( x[m,n] \)을 2차원 신호라고 한다. 2차원 신호에서 인덱스는 주로 공간상의 위치를 나타내는 배열 또는 순서를 뜻한다. 2차원 신호는 행렬로 나타내며 \( m \)은 행, \( n \)은 열을 나타낸다. 대표적인 2차원 신호로는 이미지(image) 신호가 있다.

2차원 신호와 관련된 컨볼루션을 2D 컨볼루션이라고 한다. 지금부터 LTI(linear time-invariant) 시스템과 1D 컨볼루션에서 다루었던 내용을 그대로 이용하여 LSI(linear shift-invariant) 시스템과 2D 컨볼루션의 관계를 설명하고자 한다. 복습한다고 생각하고 읽어주기 바란다.
2020/07/23 - [CNN의 수학] - LTI 시스템과 컨볼루션
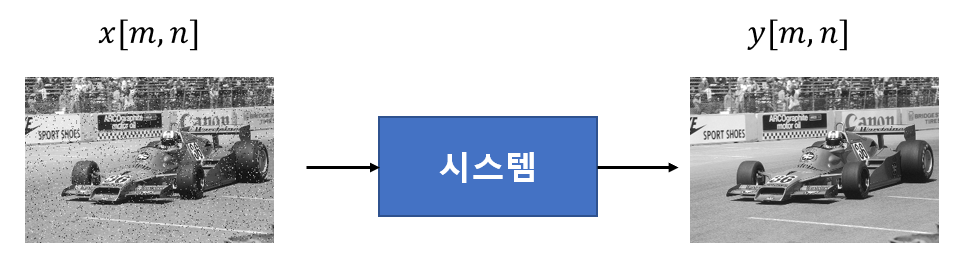
수학적으로 시스템은 2차원 입력신호에서 2차원 출력신호를 연결하는 연산자(operator) \( \mathcal{F} \)로 표현할 수 있다.
\[ y[m,n]= \mathcal{F} \{ x[m,n] \} \]
시스템이 중첩의 원리를 만족하면 선형(linear) 시스템이라고 한다. 중첩의 원리는 다음과 같은 것이다.
\( y_1[m,n]= \mathcal{F} \{ x_1[m,n] \}, \quad y_2[m,n]=\mathcal{F} \{ x_2[m,n] \} \) 일 때,
\[ \begin{align} \mathcal{F} \{ \alpha_1 x_1[m,n] + \alpha_2 x_2[m,n] \} &= \alpha_1 \mathcal{F} \{ x_1[m,n] \} + \alpha_2 \mathcal{F} \{x_2[m,n] \} \\ \\ &= \alpha_1 y_1[m,n] + \alpha_2 y_2 [m,n] \end{align} \]
이면, \( \mathcal{F} \)는 선형 시스템이다.
인덱스가 시간일 때 사용한 시불변(time-invariant)이라는 용어 대신에 인덱스가 공간일 때에는 시프트-불변(shift-invariant)이라는 용어를 사용한다. 의미는 똑같다. 시프트-불변 시스템을 수식으로 표현하면 다음과 같다.
\( y[m,n]=F\{x[m,n]\} \) 일 때,
\( y[m-m_0,n-n_0 ]= \mathcal{F} \{x[m-m_0,n-n_0 ] \} \) 이면,
\( \mathcal{F} \)는 시프트-불변 시스템이다.
시스템이 선형(linear)이고 시프트-불변(shift-invariant)이라면 LSI 시스템이라고 한다.
이제 LSI 시스템에 임의의 입력 \( x[m,n] \)을 가했을 때 출력 \( y[m,n] \)이 어떻게 계산되는지 알아보자. 그 전에 먼저 2차원 임펄스(impulse) 신호에 대해 알아보자.
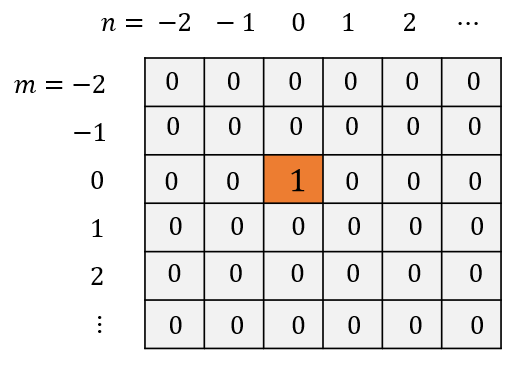
2차원 임펄스 신호는 \( m=0 \), \( n=0 \)일 때만 크기가 1이고, \( m \ne 0 \) 또는 \( n \ne 0 \)에서는 크기가 모두 0인 신호다. 기호로 \( \delta [m,n] \)이라 쓴다. 크기가 1이므로 단위 임펄스라고 하기도 한다.
임펄스를 수식으로 표현하면 다음과 같다.
\[ \delta [m,n]= \begin{cases} 1, & \mbox{if }m=0 \mbox{ and } n=0 \\ 0, & \mbox{if }m \ne 0 \mbox{ or } n \ne 0 \end{cases} \]
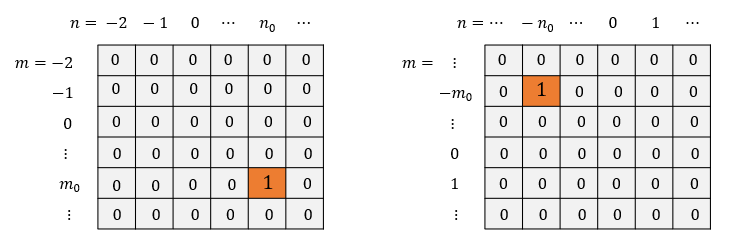
2차원 임펄스 신호를 오른쪽과 아래로 \( m_0 \), \( n_0 \) 만큼 시프트(shift)시킨 신호는 \( \delta [m-m_0,n-n_0 ] \)이다. 임펄스 신호를 왼쪽과 위로 \( m_0 \), \( n_0 \) 만큼 시프트시킨 신호는 \( \delta [m+m_0,n+n_0 ] \)이다. 아래 그림의 왼쪽은 \( \delta [m-m_0,n-n_0 ] \)를 오른쪽은 \( \delta [m+m_0,n+n_0 ] \)를 그린 것이다.
임의의 입력 신호 \( x[m,n] \)은 다음과 같이 임펄스 신호를 이용한 수식으로 표현할 수 있다.
\[ \begin{align} x[m,n] &= ⋯ +x[-2,-2] \delta[m+2,n+2]+x[-2,-1] \delta [m+2,n+1] \\ \\ & \quad +x[-2,0] \delta [m+2,n]+x[-2,1] \delta [m+2,n-1]+ ⋯ \\ \\ & \quad +x[-1,-2] \delta [m+1,n+2] + x[-1,-1] \delta [m+1,n+1]+ ⋯ \end{align} \]
위 식은 덧셈이 무한히 이어지는 식이라서 쓰기 불편하므로 시그마 기호를 이용해서 간단하게 다음과 같이 표현한다.
\[ x[m,n] = \sum_{k=-\infty}^\infty \sum_{l=-\infty}^\infty x[k,l] \delta[m-k, n-l] \]
임펄스 신호의 특성상 \( k=m \),\( l=n \)에서만 \( \delta [m-k,n-l]=1 \)이고 나머지는 모두 0이므로 위 식의 좌우변이 같다는 것을 알 수 있다.
이제 2차원 임펄스를 LSI 시스템의 입력으로 가해보자. 이 때 출력을 임펄스 반응(impulse response) 또는 점 확산 함수(point spread function)라고 하며 기호로 \( h[m,n] \)이라 쓴다.
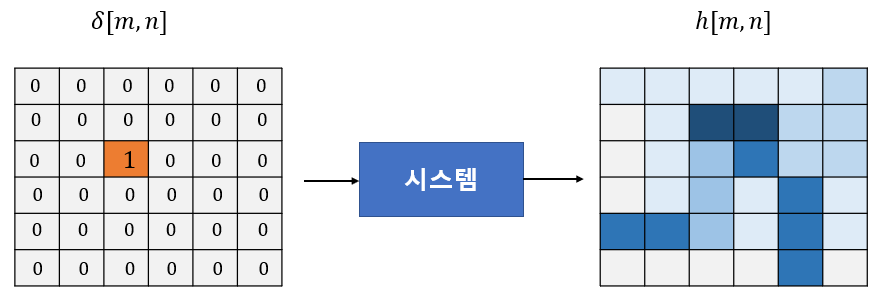
수식으로 표현하면 다음과 같다.
\[ h[m,n]= \mathcal{F} \{ \delta [m,n] \} \]
이제 시스템에 임의의 입력 \( x[n] \)을 가했을 때 출력을 수식으로 써보자.
\[ y[m,n]= \mathcal{F} \{ x[m,n] \} \]
임의의 입력 신호 \( x[m,n] \)을 임펄스 신호를 이용한 수식으로 표현할 수 있다고 했으므로, 위 식은 다음과 같이 쓸 수 있다.
\[ \begin{align} y[m,n] &= \mathcal{F} \{ x[m,n] \} \\ \\ & = \mathcal{F} \{ ⋯ +x[0,-1] \delta[m,n+1]+x[0,0] \delta [m,n] + x[0,1] \delta [m,n-1]+ ⋯ \\ \\ & = \mathcal{F} \{ \sum_{k=-\infty}^\infty \sum_{l=-\infty}^\infty x[k,l] \delta[m-k, n-l] \} \end{align} \]
만약 시스템이 선형이라면, 중첩의 원리가 적용되므로 위 식은 다음과 같이 된다.
\[ \begin{align} y[m,n] & = ⋯ +x[0,-1] \mathcal{F} \{ \delta[m,n+1] \} + x[0,0] \mathcal{F} \{ \delta [m,n] \} + x[0,1] \mathcal{F} \{ \delta [m,n-1] \} + ⋯ \\ \\ & = \sum_{k=-\infty}^\infty \sum_{l=-\infty}^\infty x[k,l] \mathcal{F} \{ \delta[m-k, n-l] \} \end{align} \]
또한 이에 덧붙여서 시스템이 시프트-불변이라면 위 시스템은 다음과 같이 된다.
\[ \begin{align} y[m,n] & = ⋯ +x[0,-1] h[m,n+1] + x[0,0] h[m,n] + x[0,1] h[m,n-1] + ⋯ \\ \\ & = \sum_{k=-\infty}^\infty \sum_{l=-\infty}^\infty x[k,l] h[m-k, n-l] \end{align} \]
따라서 LSI 시스템의 입력이 \( x[m,n] \)일 때 출력 \( y[m,n] \)은 다음과 같이 된다.
\[ y[m,n] = \sum_{k=-\infty}^\infty \sum_{l=-\infty}^\infty x[k,l] h[m-k, n-l] \]
여기서 2차원 컨볼루션을 다음과 같이 정의하면,
\[ h[m,n] * x[m,n] = \sum_{k=-\infty}^\infty \sum_{l=-\infty}^\infty x[k,l] h[m-k, n-l] \]
LSI 시스템의 출력은 시스템의 임펄스 반응과 입력의 컨볼루션이다.
\[ y[m,n] = h[m,n] * x[m,n] \]
LSI 시스템의 임펄스 반응에는 시스템의 모든 정보가 담겨져 있다. LSI 시스템의 임펄스 반응은 시스템 그 자체다.
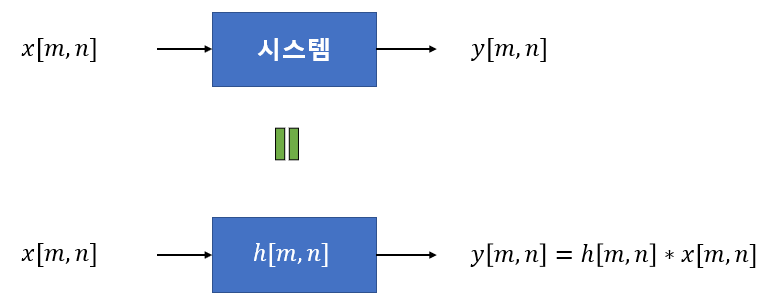
이미지 처리 분야에서는 LSI 시스템을 이미지 필터 또는 2D 커널이라고 부른다.
'AI 딥러닝 > DLA' 카테고리의 다른 글
| [CNN] 이미지 필터 설계해 보기 (0) | 2020.07.29 |
|---|---|
| [CNN] 2D 컨볼루션 계산하기 (0) | 2020.07.29 |
| [CNN] 이동평균(moving average) 필터 설계해 보기 (0) | 2020.07.26 |
| [CNN] 컨볼루션 쉽게 계산하기 (0) | 2020.07.25 |
| [CNN] 컨볼루션 공식대로 계산하기 (0) | 2020.07.25 |




댓글