필터를 설계한다는 것은 곧 LTI 시스템의 임펄스 반응 \( h[n] \)을 결정하는 것과 같다.
주식 차트를 보면 5일 이동평균선, 10일 이동평균선이라는 것이 있다. 5일 이동 평균은 현재부터 과거 5일전까지의 주가 평균을 계산한 것이다. 10일 이동 평균선도 마찬가지로 현재부터 과거 10일전까지의 주가를 평균 낸 것이다.
그러면 주식 차트의 이동평균선과 비슷하게, 입력 신호에 대한 5 포인트(point) 이동평균 필터와 10 포인트 이동평균 필터를 설계해 보자.
입력 신호를 \( x[n] \)으로 하고, 이동 평균 출력 신호를 \( y[n] \)으로 하면 5 포인트 이동평균 필터의 임펄스 반응은 다음과 같이 설계할 수 있다.
\[ \begin{align} h[n] &= \frac{1}{5} ( \delta [n]+\delta [n-1]+\delta [n-2]+ \delta [n-3]+\delta [n-4] ) \\ \\ &= \frac{1}{5} \sum_{k=0}^4 \delta [n-k] \end{align} \]
출력 \( y[n] \)은 시스템의 임펄스 반응 \( h[n] \)과 입력 \( x[n] \)의 컨볼루션으로 주어진다.
\[ \begin{align} y[n] &=h[n] * x[n] \\ \\ &= \sum_{k=-\infty}^{\infty} h[n-k] x[k] \end{align} \]
'뒤집기 와 이동' 방법을 사용하여 컨볼루션을 계산하기 위해서 먼저 임펄스 반응을 뒤집으면,
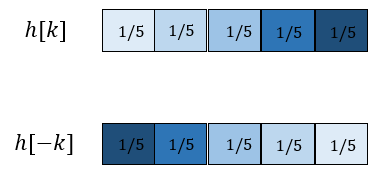
가 된다.
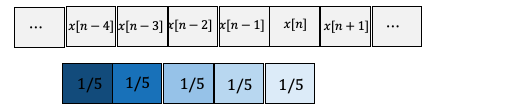
\( x[n] \) 영역의 처음부터 빠져나갈 때까지 \( h[n] \)을 이동하며 겹치는 부분을 곱셈과 덧셈을 반복하여 컨볼루션을 계산하면,




가 되어서, 5 포인트 이동평균 필터는 어떤 입력 \( x[n] \)에 대해서 다음 출력을 생성한다.
\[ \begin{align} y[n] &= \frac{1}{5} ( x[n]+x[n-1]+x[n-2]+x[n-3]+x[n-4] ) \\ \\ &= \frac{1}{5} \sum_{k=0}^4 x[n-k] \end{align} \]
시간스텝 \( n \)에서의 출력은 시간스텝 \( n \)에서의 입력부터 4단계의 시간스텝 전까지의 입력을 모두 더한 후 5로 나눈 것이다.
비슷한 방법으로 10 포인트 이동평균 필터의 임펄스 반응은 다음과 같이 설계할 수 있으며,
\[ h[n] = \frac{1}{10} \sum_{k=0}^9 \delta [n-k] \]
출력 \( y[n] \)은 시스템의 임펄스 반응 \( h[n] \)과 입력 \( x[n] \)의 컨볼루션을 계산하면, 10 포인트 이동평균 필터는 어떤 입력 \( x[n] \)에 대해서 다음 출력을 생성한다.
\[ y[n] = \frac{1}{10} \sum_{k=0}^9 x[n-k] \]
예로서 아래 그림과 같은 입력 신호 \( x[n] \)에 대해서
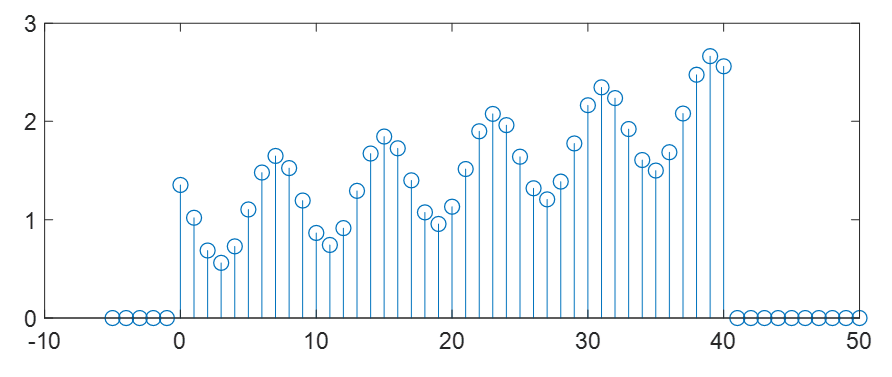
5 포인트 이동평균은 아래 그림과 같고,
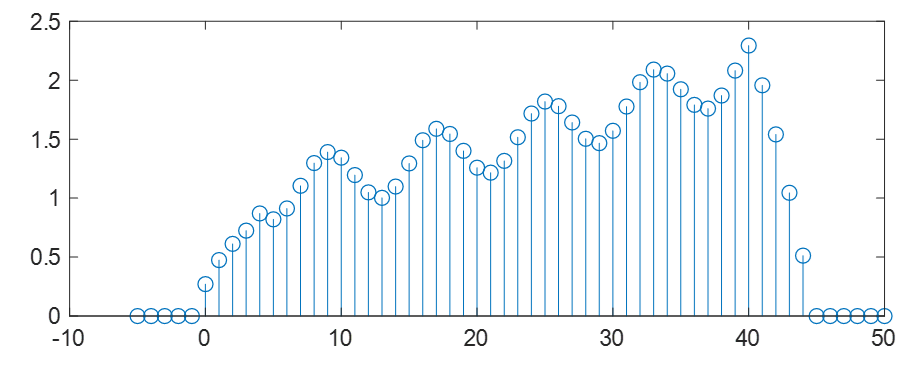
10 포인트 이동평균은 아래 그림과 같다.
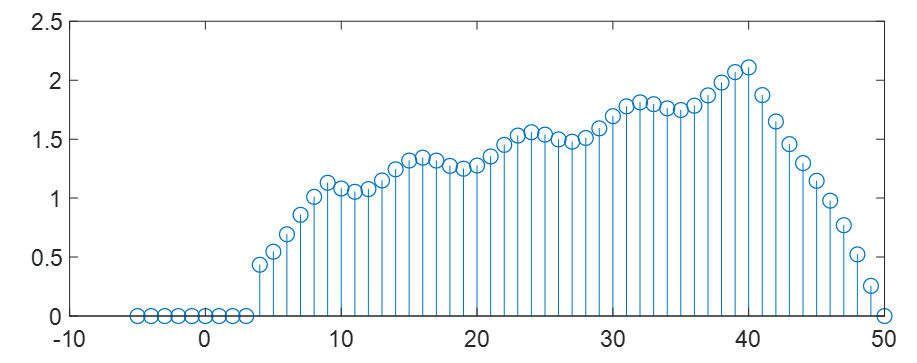
이동평균 필터는 저주파 통과 필터로서 입력 신호의 빠른 변화를 부드럽게 바꿔준다. 평균 계산 구간이 길수록 필터링된 신호의 변화가 더 완만하다.
'AI 딥러닝 > DLA' 카테고리의 다른 글
| [CNN] 2D 컨볼루션 계산하기 (0) | 2020.07.29 |
|---|---|
| [CNN] 2D 컨볼루션 (0) | 2020.07.28 |
| [CNN] 컨볼루션 쉽게 계산하기 (0) | 2020.07.25 |
| [CNN] 컨볼루션 공식대로 계산하기 (0) | 2020.07.25 |
| [CNN] LTI 시스템과 컨볼루션 (0) | 2020.07.23 |




댓글