1D 컨볼루션과 똑같은 방법으로 '뒤집기와 이동' 방법을 사용하여 2D 컨볼루션을 계산해보자.
2020/07/25 - [CNN의 수학] - 컨볼루션 쉽게 계산하기
공식을 살펴보면,
\[ y[m,n] = \sum_{k=-\infty}^\infty \sum_{l=-\infty}^\infty x[k,l] h[m-k, n-l] \]
우선 \( x[m,n] \)과 \( h[m,n] \)을 \( x[k,l] \)과 \( h[k,l] \)로 바꿔야 한다는 것을 알 수 있다.
그리고 \( h[k,l] \)을 수평축과 수직축을 기준으로 두 번 뒤집어서 \( h[-k,-l] \)로 만든 후,
\( m,n \)만큼 수평과 수직으로 이동시켜서 \( h[m-k,n-l] \)을 만들고,
\( k,l \)에 대해서 \( x[k,l] \)과 \( h[m-k,n-l] \)를 곱한 다음,
\( k,l \)에 대해서 \( h[m-k,n-l]x[k,l] \)를 모두 더하면 \( y[m,n] \)을 계산할 수 있다.
그리고 모든 \( m,n \)에 대해서 위 과정을 반복하면 된다.
그럼 해 보자.
다음과 같이 2D 임펄스 반응과 2D 입력 신호가 있다고 하자.

\( x[m,n] \)과 \( h[m,n] \)을 \( x[k,l] \)과 \( h[k,l] \)로 바꾼다.

\( h[k,l] \)을 수평축을 기준으로 뒤집어서 \( h[-k,l] \)을 만든다.
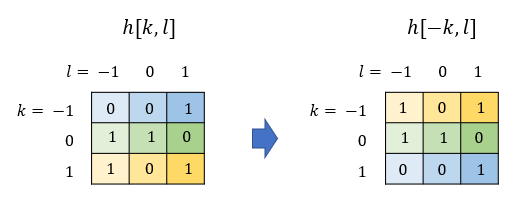
\( h[-k,l] \)을 수직축을 기준으로 뒤집어서 \( h[-k,-l] \)을 만든다.

그리고 \( m,n \)만큼 수평과 수직으로 이동시켜서 \( h[m-k,n-l] \)을 만든다.

\( m=-1,n=-1 \)에서 \( k,l \)에 대해서 \( x[k,l] \)과 \( h[m-k,n-l] \)을 곱하고 더한다.
\[ y[-1,-1] = 0(1)=0 \]

오른쪽으로 한 스텝 이동하여 \( m=-1,n=0 \)에서 \( k,l \)에 대해서 \( x[k,l] \)과 \( h[m-k,n-l] \)을 곱하고 더한다.
\[ y[-1,0] = 0(1)+0(2)=0 \]
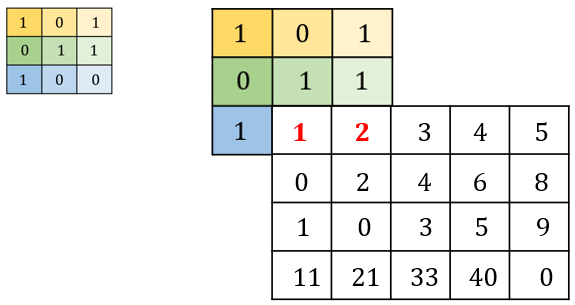
오른쪽으로 한 스텝 이동하여 \( m=-1,n=1 \)에서 \( k,l \)에 대해서 \( x[k,l] \)과 \( h[m-k,n-l] \)을 곱하고 더한다.
\[ y[-1,1] = 1(1)+0(2)+0(3)=1 \]

계속 진행해서, \( m=-1,n=5 \)에서 \( k,l \)에 대해서 \( x[k,l] \)과 \( h[m-k,n-l] \)을 곱하고 더한다.
\[ y[-1,5] = 1(5)=5 \]

다음으로 아래쪽으로 한 스텝 이동하여 \( m=0,n=-1 \)에서 \( k,l \)에 대해서 \( x[k,l] \)과 \( h[m-k,n-l] \)을 곱하고 더한다.
\[ y[0,-1] = 1(1)+0(0)=1 \]

다음으로 오른쪽으로 한 스텝 이동하여 \( m=0,n=0 \)에서 \( k,l \)에 대해서 \( x[k,l] \)과 \( h[m-k,n-l] \)을 곱하고 더한다.
\[ y[0,0] = 1(1)+1(2)+0(0)+0(2)=3 \]

계속 진행해서 \( m=2,n=3 \)에서 \( k,l \)에 대해서 \( x[k,l] \)과 \( h[m-k,n-l] \)을 곱하고 더한다.
\[ y[2,3]=1(4)+0(6)+1(8)+0(3)+1(5)+1(9)+1(33)+0(40)+0(0)=59 \]
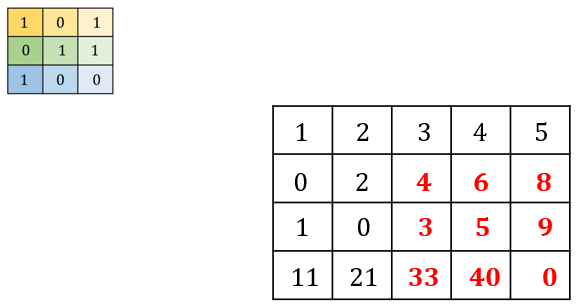
이런 식으로 \( h[m-k,n-l] \)이 \( x[k,l] \)영역을 빠져나갈 때까지 계속 반복한다.
\[ y[4,5]=0(0)=0 \]

그러면 2D 출력 신호 \( y[m,n] \)은 다음과 같이 계산된다.

2D 컨볼루션을 계산할 때, 임펄스 반응 (또는 2D 커널)과 겹치는 입력 신호가 없을 경우에는 신호 값이 0이라고 간주했는데 이와 같이 여분의 0을 추가하는 과정을 제로 패딩(zero padding)이라고 한다.
'AI 딥러닝 > DLA' 카테고리의 다른 글
| [CNN] 컨볼루션과 상관도 (0) | 2020.09.22 |
|---|---|
| [CNN] 이미지 필터 설계해 보기 (0) | 2020.07.29 |
| [CNN] 2D 컨볼루션 (0) | 2020.07.28 |
| [CNN] 이동평균(moving average) 필터 설계해 보기 (0) | 2020.07.26 |
| [CNN] 컨볼루션 쉽게 계산하기 (0) | 2020.07.25 |




댓글