필터를 설계한다는 것은 곧 LSI 시스템의 임펄스 반응 \( h[m,n] \)을 결정하는 것과 같다. 그러면 입력 이미지가 \( x[m,n] \)일 때, 필터링된 출력 이미지 \( y[m,n] \)은 시스템의 임펄스 반응과 입력 이미지의 2D 컨볼루션으로 주어진다.
\[ \begin{align} y[m,n] &= h[m,n]*x[m,n] \\ \\ &= \sum_{k =-\infty}^{\infty} \sum_{l =-\infty}^{\infty} x[k,l] h[m-k,n-l] \end{align} \]
간단히 3개의 이미지 필터를 설계해 보자.
먼저 이미지를 흐릿하게 만드는 스무딩(smoothing) 필터다. 스무딩 필터의 임펄스 반응은 다음과 같이 정할 수 있다.

임펄스 반응을 보면 스무딩 필터는 필터의 중심점을 기준으로 주변 픽셀의 평균값을 계산한다는 것을 알 수 있다. 따라서 이미지가 흐릿해지리라는 것을 짐작할 수 있다. 주파수 영역에서 보면 스무딩 필터는 저주파 통과 필터라는 것을 금방 알 수 있다.
아래와 같은 선명한 레이싱카 이미지가 이 필터를 통과한 후에는

약간 흐릿하게 바뀐다.

이번에는 이미지의 윤곽선을 추출할 수 있는 샤프닝(sharpening) 필터다. 샤프닝 필터는 고주파 통과 필터로서 임펄스 반응을 다음과 같이 정할 수 있다.
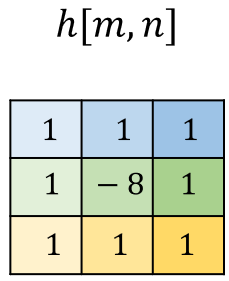
레이싱카 이미지가 필터를 통과한 후에는 다음과 같이 바뀐다.

마지막으로 이미지의 가로선을 검출할 수 있는 필터다. 세로 방향의 픽셀 차이를 계산하므로 이미지에서 가로선을 검출할 수 있다.

레이싱카 이미지는 다음과 같이 바뀐다.

'AI 딥러닝 > DLA' 카테고리의 다른 글
| [PINN] 물리 정보 신경망 (Physics-Informed Neural Network) (0) | 2021.09.19 |
|---|---|
| [CNN] 컨볼루션과 상관도 (0) | 2020.09.22 |
| [CNN] 2D 컨볼루션 계산하기 (0) | 2020.07.29 |
| [CNN] 2D 컨볼루션 (0) | 2020.07.28 |
| [CNN] 이동평균(moving average) 필터 설계해 보기 (0) | 2020.07.26 |




댓글