일반적으로 많이 쓰이는 ‘뒤집기와 이동’ 방법을 사용하여 컨볼루션을 계산해 보자.
공식을 잘 살펴보면,
\[ y[n] = \sum_{k=-\infty}^\infty h[n-k] x[k] \]
우선 \( x[n] \)과 \( h[n] \)을 \(x[k] \)와 \( h[k] \)로 바꿔야 한다는 것을 알 수 있다. 그리고, \( h[k] \)를 뒤집어서 \( h[-k] \)로 만든 후, \( n \)만큼 이동시켜서 \( h[n-k] \)를 만든 후, \( k \)에 대해서 \( x[k] \)와 \( h[n-k] \)를 곱한 다음, \( k \)에 대해서 \( h[n-k]x[k] \)를 모두 더하면 \( y[n] \)을 계산할 수 있다는 것을 알 수 있다. 그리고, 모든 \( n \)에 대해서 위 과정을 반복하면 된다.
그럼 해 보자.
다음과 같이 임펄스 반응과 입력 신호가 있다고 하자.
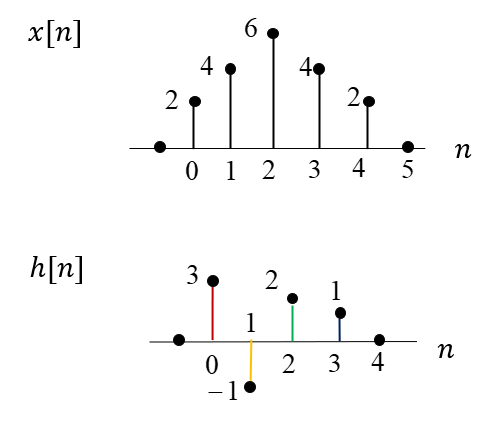
\( h[n] \)과 \( x[n] \)을 \( h[k] \)와 \( x[k] \)로 바꾼다.

\( h[k] \)를 뒤집고 이동시켜서 \( h[n-k] \)를 만든다.
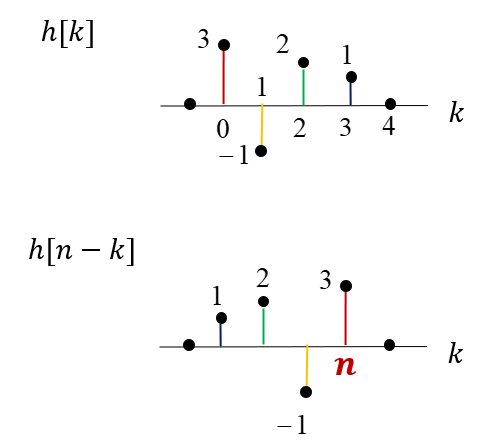
\( n=0 \)에서 \( k \)에 대해서 \( x[k] \)와 \( h[n-k] \)를 곱하고 더한다.

\( n=1 \)에서 \( k \)에 대해서 \( x[k] \)와 \( h[n-k] \)를 곱하고 더한다.

\( n=2 \)에서 \( k \)에 대해서 \( x[k] \)와 \( h[n-k] \)를 곱하고 더한다.

이런 식으로 \( h[n-k] \)가 \( x[k] \)영역을 빠져나갈 때까지 계속 반복한다.
\( n=7 \)에서는,
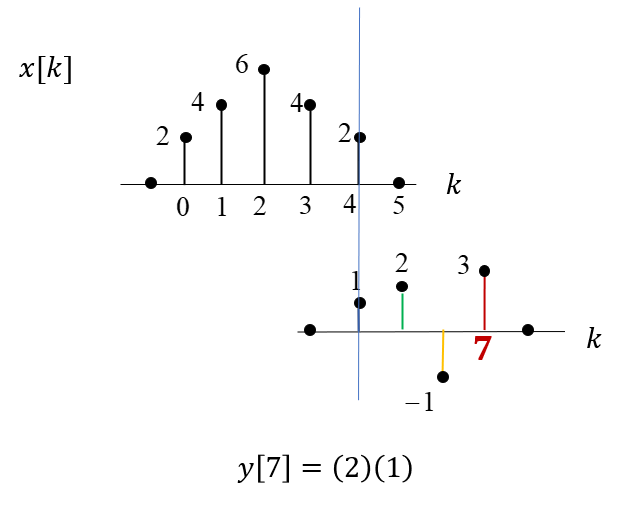
\( n=8 \)에서는 \( h[n-k] \)가 \( x[k] \)영역을 완전히 빠져나간다.

컨볼루션 계산 결과는 동일하다. 하지만 '뒤집기와 이동' 방법이 이해하기는 쉽다.
정리하면 다음과 같다.
입력 신호와 임펄스 응답이 다음과 같을 때,

컨볼루션은 다음과 같이 \( h[n] \)을 뒤집어서

\( x[n] \)영역의 처음부터 빠져나갈 때까지\( h[n] \)을 이동하며 겹치는 부분을 곱셈과 덧셈을 반복하여 계산한다.

'AI 딥러닝 > DLA' 카테고리의 다른 글
| [CNN] 2D 컨볼루션 (0) | 2020.07.28 |
|---|---|
| [CNN] 이동평균(moving average) 필터 설계해 보기 (0) | 2020.07.26 |
| [CNN] 컨볼루션 공식대로 계산하기 (0) | 2020.07.25 |
| [CNN] LTI 시스템과 컨볼루션 (0) | 2020.07.23 |
| [CNN] LTI 시스템 – 시불변 (0) | 2020.07.21 |




댓글