풍력단지 제어(Wind Farm Control)의 방법

풍력단지에서 전력 손실의 가장 큰 원인 중의 하나는 상류 풍력터빈에 의해 발생하는 후류(wake)로서, 이로 인해 전체 전력의 약 20~40% 가량이 손실된다고 한다. 뿐만 아니라 하류에 있는 풍력터빈은 상류 풍력터빈 보다도 약 80% 가량 더 큰 구조적 하중(loading)을 받는다고 한다.

 

 

이러한 문제에 대처하기 위한 풍력단지 제어(wind farm control)로서 일반적으로 두가지 방법이 사용된다. 후류방향제어(WRC, Wake Redirection Control)와 축방향 유도제어(AIC, Axial Induction Control)이다. 연구에 따르면 두 방법 모두 전력 생산을 증가시킬 수 있고 구조적 하중을 줄일 수 있다고 한다.

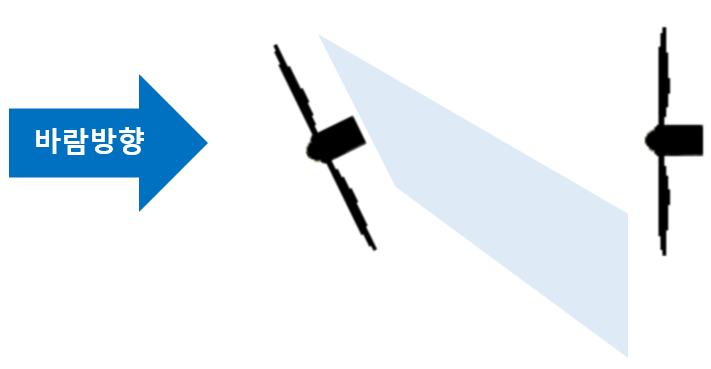
후류방향제어(WRC)는 상류 풍력터빈의 로터면을 유입되는 바람과 의도적으로 부정렬(요잉, yawing)시켜 후류의 방향으로 바꾸어서 하류의 풍력터빈이 후류와 겹치지 않거나 또는 부분적으로 겹치게 하는 제어 방법이다. 요제어(yaw control)를 이용하여 유입되는 바람과 로터면을 부정렬시킬 수 있다. 바람을 맞고 있는 풍력터빈을 요잉시키면 전력 생산이 감소하지만 풍력단지 전체의 총 전력 생산은 증가할 수 있다. 연구 결과에 의하면 WRC는 연간 전력 생산을 약 3~4% 가량 증가시켰다고 한다.

 

 

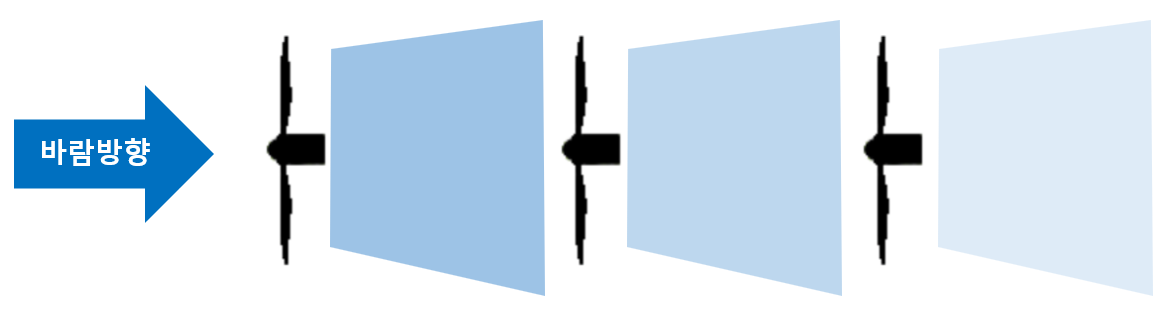
축방향유도제어(AIC, axial induction control)는 축방향 유도계수를 변경하여 하류 풍력터빈이 전력을 더 많이 생성할 수 있도록 상류 풍력터빈의 전력 생산을 줄이는 제어 방법이다. 축 방향 유도계수는 블레이드 피치각과 발전기 토크를 조종하여 바꿀 수 있다.

 

 

언뜻 생각하면 상류 풍력터빈의 전력 생산을 줄여서 하류 풍력터빈의 전력 생산을 늘린다고 해서 풍력단지의 총 전력 생산이 증가될 수 있을까 하는 의구심이 들 수 있다. 이와 관련하여 UT Dallas의 Rotea교수의 논문 “Dynamic Programming Framework for Wind Power Maximization”에 나와 있는 대로 이상적인 풍력터빈 모델과 단지 모델을 이용하여 축방향유도제어(AIC)의 유효성을 알아보자.

액추에이터 평판모델(ADM, actuator disk model)에 의하면 일정한 바람 속도 $v$ 가 불어올 때, 풍력터빈으로부터 멀리 떨어진 곳의 하류(far wake) 속도는 $v_f=v-2av$ 이고 풍력터빈이 생산하는 전력은 $P=2\rho A{v}^2(1-a{)}^{2}av$ 이다. 여기서 $\rho$ 는 공기 밀도, $A$ 는 로터 회전 단면적, $a$ 는 축방향 유도계수이다.

 

 

만약, 풍력터빈 $N$ 개가 바람의 진행 방향으로 서로 충분히 멀리 떨어진 거리에서 일렬로 늘어서 있다면 각 터빈의 상류 속도와 하류 속도는 다음과 같다.

 

$$\begin{array}{r}\text{(1)}& & v_1=v_0-2a_0{v}_0\\ & v_2=v_1-2a_1{v}_1\\ & ⋮\\ & v_{k+1}=v_k-2a_k{v}_k\\ & ⋮\\ & v_N=v_{N-1}-2a_{N-1}{v}_{N-1}\end{array}$$

 

여기서 $v_k$ 는 맨 앞에서부터 $k$ 번째 풍력터빈의 상류 바람속도이며 이 속도는 $k-1$ 번째 풍력터빈의 하류 바람속도와 같다.

 

 

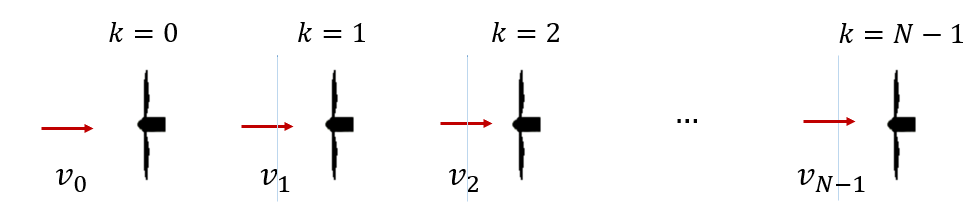
맨 처음 풍력터빈은 $0$ 번째 터빈으로서 $v_0$ 는 $0$ 번째 풍력터빈의 상류 속도이자 풍력단지로 불어오는 바람(자유류)의 속도이기도 하다. $a_k$ 는 $k$ 번째 풍력터빈의 축방향 유도계수이며, $k$ 번째 풍력터빈이 생산하는 파워는 다음과 같다.

 

$$\begin{array}{}\text{(2)}& P_k=2\rho A{v}_k^2(1-a_k{)}^2{a}_k{v}_k\end{array}$$

 

식 (1)과 (2)에 의하면 각 풍력터빈의 축방향 유도계수를 조절하면 터빈의 하류 바람속도와 전력 생산량이 달라진다. 따라서 축방향 유도계수를 제어변수로 고려하는 것이 자연스러운 선택이다.

 

 

하지만 시스템의 선형성을 유지하기 위해서는 축방향 유도계수와 바람 속도의 곱을 제어변수로 설정하는 것이 유리할 것이다. 즉, 제어변수를 다음과 같이 정의한다.

 

$$\begin{array}{}\text{(3)}& u_k=a_k{v}_k\end{array}$$

 

그러면 축방향 유도계수는 제어기의 게인(gain)이 되며 시스템은 상태변수 피드백 제어의 형태가 된다.

여기서 최적제어에서 사용되는 표준 기호를 사용하기 위해 $x_k=v_k$ 로 놓고 식 (1)을 상태변수 방정식 형태로 쓰면 다음과 같다.

 

$$\begin{array}{}\text{(4)}& x_{k+1}=x_k-2u_k,x_0\text{given}\end{array}$$

 

이 시스템이 최대화해야 할 목적함수는 모든 터빈이 생산하는 전력의 총합이다.

 

$$\begin{array}{r}\text{(5)}& J(x_0)& =\sum _{k=0}^{N-1}{P}_k\\ & =2\rho A\sum _{k=0}^{N-1}(x_k-u_k{)}^2{u}_k\end{array}$$

 

최적제어 또는 강화학습의 용어를 사용하면 각 풍력터빈이 생산하는 전력은 보상(reward)함수 $r(x_k,u_k)$ 가 되고 목적함수는 총 누적보상(accumulated reward)된다.

축방향 유도계수의 유효 범위가 $0\le a\le \frac{1}{2}$ 이기 때문에 시스템 입력의 제약조건은 다음과 같다.

 

$$\begin{array}{}\text{(6)}& 0\le u_k\le \frac{1}{2}{x}_k\end{array}$$

 

식 (4)와 (5)로 주어지는 최적제어 문제를 풀기 위해 벨만(Bellman)의 최적성 원리(optimality principle)에 기반한 다이내믹 프로그래밍(dynamic programming)을 이용한다. 우선 목적함수를 스텝(여기서는 풍력터빈의 인덱스) $k$ 를 기준으로 다음과 같이 분리한다.

 

$$\begin{array}{r}\text{(7)}& J_k& =\sum _{t=k}^{N-1}r(x_t,u_t)\\ & =r(x_k,u_k)+\sum _{t=k+1}^{N-1}r(x_t,u_t)\\ \\ & =r(x_k,u_k)+J_{k+1}\end{array}$$

 

여기서 $J_k$ 는 스텝 $k$ 에서의 잔여 보상(reward-to-go)을 나타낸다. 위 식에서 현재 스텝 $k$ 의 보상함수가 다음 스텝 $k+1$ 의 보상함수의 관계식으로 나타나는 반복성(recurrency)을 가지고 있으며, 역방향-스텝의 관점에서는 목적함수가 재귀적(recursion)으로 표현됨을 알 수 있다. 식 (7)을 벨만 방정식이라고 한다.

이제 최적제어 $u_{k+1}^{\star },u_{k+2}^{\star },...,u_{N-1}^{\star }$ 을 적용해 다음 스텝 $k+1$ 부터 최종 스텝 $N-1$ 까지 최대의 누적 보상을 실현했다고 가정한다. 그러면 스텝 $k$ 의 누적보상은 다음과 같다.

 

$$\begin{array}{}\text{(8)}& J_k=r(x_k,u_k)+J_{k+1}^{\star }\end{array}$$

 

벨만의 최적성 원리에 의하면 스텝 $k$ 에서 최종 스텝 $N-1$ 까지 최대의 누적보상을 실현하는 스텝 $k$ 의 최적제어는 다음 식을 만족해야 한다.

 

$$\begin{array}{}\text{(9)}& J_k^{\star }=\underset{u_k}{max}(r(x_k,u_k)+J_{k+1}^{\star })\end{array}$$

 

위 식을 벨만 최적 방정식이라고 한다. 위 식에 의하면 $J_{k+1}^{\star }$ 을 알아야 스텝 $k$ 의 $J_k^{\star }$ 를 계산할 수 있다. 즉, 벨만 최적 방정식에 의하면 최종 스텝에서 초기 스텝으로 거슬러 올라가며 최적제어 전략을 결정해야 한다.

최종 스텝인 $k=N-1$ 에서는 보상이 다음과 같다.

 

$$\begin{array}{r}\text{(10)}& J_{N-1}& =r(x_{N-1},u_{N-1})\\ & =(x_{N-1}-u_{N-1}{)}^2{u}_{N-1}\end{array}$$

 

위 함수를 최대로 만드는 최적제어 $u_{N-1}^{\star }$ 를 구하기 위해 다음과 같이 미분을 수행한다.

 

$$\begin{array}{}\text{(11)}& 0=\frac{\partial J_{N-1}}{\partial u_{N-1}}=(x_{N-1}-u_{N-1}{)}^2-2(x_{N-1}-u_{N-1})u_{N-1}\end{array}$$

 

그러면 $u_{N-1}^{\star }$ 은 다음과 같이 구해진다.

 

$$\begin{array}{}\text{(12)}& u_{N-1}^{\star }=\frac{1}{3}{x}_{N-1}=a_{N-1}{x}_{N-1}\end{array}$$

 

여기서 $a_{N-1}=\frac{1}{3}$ 이다. 식 (12)를 (10)에 대입하면 최대 누적보상 값을 구할 수 있다.

 

$$\begin{array}{}\text{(13)}& J_{N-1}^{\star }=\frac{4}{27}{x}_{N-1}^3=Q_{N-1}{x}_{N-1}^3\end{array}$$

 

여기서 $Q_{N-1}=\frac{4}{27}$ 이다. 다음으로 스텝 $k=N-2$ 에서 누적보상 함수는 다음과 같다.

 

$$\begin{array}{r}\text{(14)}& J_{N-2}& =Q_{N-1}{x}_{N-1}^3+(x_{N-2}-u_{N-2}{)}^2{u}_{N-2}\\ & =Q_{N-1}(x_{N-2}-2u_{N-2}{)}^3+(x_{N-2}-u_{N-2}{)}^2{u}_{N-2}\end{array}$$

 

위 함수를 최대로 만드는 최적제어 $u_{N-2}$ 를 구하기 위해 다음과 같이 미분을 수행한다.

 

$$\begin{array}{r}\text{(15)}& 0& =\frac{\partial J_{N-2}}{\partial u_{N-2}}\\ & =-6Q_{N-1}(x_{N-2}-2u_{N-2}{)}^2+(x_{N-2}-u_{N-2}{)}^2\\ \\ & -2(x_{N-2}-u_{N-2})u_{N-2}\\ \\ & =(1-6Q_{N-1})(x_{N-2}-2u_{N-2}{)}^2-u_{N-2}^2\end{array}$$

 

그러면 $u_{N-2}^{\star }$ 는 다음과 같이 구해진다.

 

$$\begin{array}{}\text{(16)}& u_{N-2}^{\star }=\sqrt{(1-6Q_{N-1})}(x_{N-2}-2u_{N-2}^{\star })\end{array}$$

 

위 식을 명시적인 값으로 표시하면 다음과 같다.

 

$$\begin{array}{r}\text{(17)}& u_{N-2}^{\star }& =\frac{\sqrt{(1-6Q_{N-1})}}{1+2\sqrt{(1-6Q_{N-1})}}{x}_{N-2}\\ & =a_{N-2}{x}_{N-2}\end{array}$$

 

여기서 $a_{N-2}$ 는 위 수식에서 $x_{N-2}$ 의 계수이다. 식 (17)을 (14)에 대입하면 최대 누적보상 값을 구할 수 있다.

 

$$\begin{array}{r}\text{(18)}& J_{N-2}^{\star }& =Q_{N-1}(1-2a_{N-2}{)}^3{x}_{N-2}^3+(1-a_{N-2}{)}^2{a}_{N-2}{x}_{N-2}^3\\ & =Q_{N-2}{x}_{N-2}^3\end{array}$$

 

마찬가지로 $Q_{N-2}$ 는 위 수식에서 $x_{N-2}^3$ 의 계수이다.

 

 

여기서 주목할 점은 $k=N-2$ 의 최대 보상 $J_{N-2}^{\star }$ 의 식 (18)이 $k=N-1$ 의 최대 보상 $J_{N-1}^{\star }$ 의 식 (13)과 똑같은 형태라는 점이다. 이것은 다음 역방향 단계인 $k=N-3$ 에서의 결과도 그 형태가 똑같을 것이라는 것을 말해준다. 따라서 역방향 스텝 $k=N-1,N-2,...,1,0$ 에서의 결과는 다음과 같이 정리할 수 있다.

 

$$\begin{array}{r}\text{(19)}& & a_k=\frac{\sqrt{(1-6Q_{k+1})}}{1+2\sqrt{(1-6Q_{k+1})}}\\ & Q_k=Q_{k+1}(1-2a_k{)}^3+(1-a_k{)}^2{a}_k\end{array}$$

 

여기서 최종 조건은 다음과 같다.

 

$$\begin{array}{}\text{(20)}& Q_N=0\end{array}$$

 

최적제어 $u_0^{\star },u_1^{\star },...,u_{N-1}^{\star }$ 시퀀스를 구하기 위해서는 최종 스텝 $N-1$ 에서부터 초기 스텝 $0$ 까지 역방향으로 거슬러 올라가며 게인 $a_k$ 를 계산해 저장해둔 후, 다시 순방향 스텝으로 계산하면 된다.

 

$$\begin{array}{}\text{(21)}& u_k^{\star }=a_k{x}_k\end{array}$$

 

따라서 풍력단지로 불어오는 바람의 속도가 $v_0$ 일 때 생산할 수 있는 최대 전력(또는 최대 누적 보상값)은 다음과 같다.

 

$$\begin{array}{r}\text{(22)}& & P^{opt}=2\rho A\sum _{k=0}^{N-1}(1-a_k{)}^2{a}_k{v}_k^3\\ & v_{k+1}=(1-2a_k)v_k,v_0\text{given}\end{array}$$

 

여기서 축방향 유도계수 $a_k$ 는 식 (19)로 계산하면 된다.

 

 

참고로 풍력단지 내의 터빈이 모두 max-$C_P$ 커브를 따르는 탐욕적(greedy) 제어방식을 사용한다면, 축방향 유도계수가 모두 $a_k=\frac{1}{3}$ 이므로 풍력단지의 전력 생산량은 다음과 같이 계산된다.

 

 

 

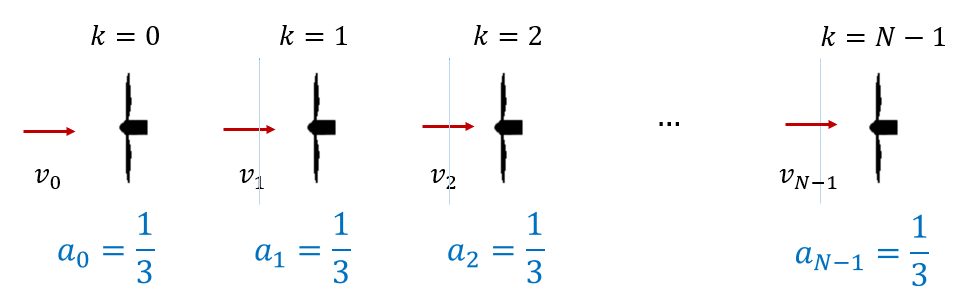
$$\begin{array}{r}\text{(23)}& P^{greedy}& =2\rho A\sum _{k=0}^{N-1}(1-a_k{)}^2{a}_k{v}_k^3\\ & =2\rho A\sum _{k=0}^{N-1}{(1-\frac{1}{3})}^2\frac{1}{3}{v}_k^3\\ \\ & =2\rho A\frac{4}{27}\sum _{k=0}^{N-1}{v}_k^3\end{array}$$

 

여기서 각 터빈의 상류 바람속도의 관계는 $v_{k+1}=\frac{1}{3}{v}_k$ 가 되므로 위 식은 다음과 같이 쓸 수 있다.

 

$$\begin{array}{r}\text{(24)}& P^{greedy}& =2\rho A\frac{4}{27}{v}_0^3\sum _{k=0}^{N-1}{\left(\frac{1}{27}\right)}^k\\ & =2\rho A\frac{4}{27}{v}_0^3\frac{1-{\left(\frac{1}{27}\right)}^N}{1-\frac{1}{27}}\end{array}$$

 

식 (24)에 의하면 풍력터빈이 $1$ 개 있을 때의 전력은 $P_1^{greedy}=2\rho A\frac{4}{27}{v}_0^3$ 인데 풍력터빈이 $N$ 개 있을 때에도 $P_N^{greedy}\approx 2\rho A\frac{4}{26}{v}_0^3$ 로서 전력 생산 증가량은 3.85% 에 불과하다.

 

$$\begin{array}{}\text{(25)}& \frac{P_N^{greedy}}{P_1^{greedy}}\approx 1.0385\end{array}$$

 

풍력터빈 $10$ 개($N=10$)를 대상으로 시뮬레이션해 보았다. 다음 그림은 $P^{greedy}$ 와 $P^{opt}$ 를 그린 것이다. 각각 $P_1^{greedy}$ 를 기준으로 정규화한 것이다. 풍력터빈의 개수가 $3$ 개 이상에서는 $P^{greedy}$ 값은 더 이상 증가하지 않지만 $P^{opt}$ 값은 계속 상승하는 것을 볼 수 있다. AIC의 유효성을 알 수 있는 결과이다.

 

 

 

 

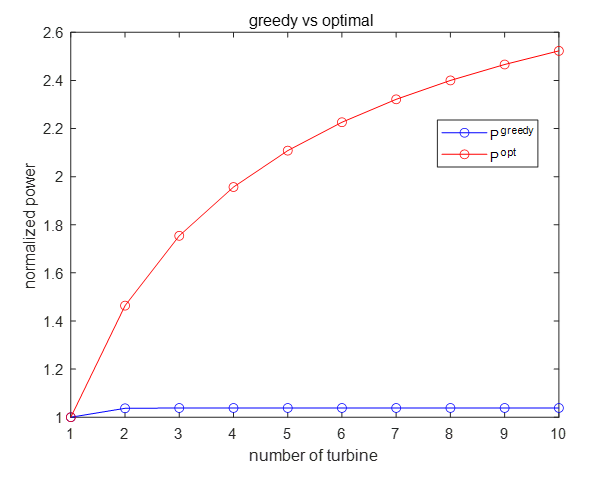
다음 그림은 $P^{opt}$ 와 $P^{greedy}$ 의 비를 그린 것이다. 풍력터빈의 개수가 늘수록 $P^{opt}$ 의 값이 $2$ 배 이상 커지는 것을 볼 수 있다.

 

 

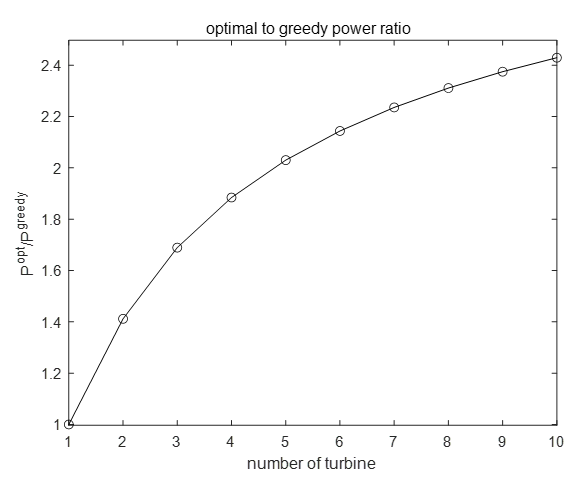
다음 그림은 각 풍력터빈의 축방향 유도계수를 그린 것이다. 상류에 있는 터빈의 유도계수를 작게 만들어서 후류의 속도를 키우고, 하류로 갈수록 유도계수를 터빈의 최적값인 $\frac{1}{3}$ 까지 증가시킨다.

 

 

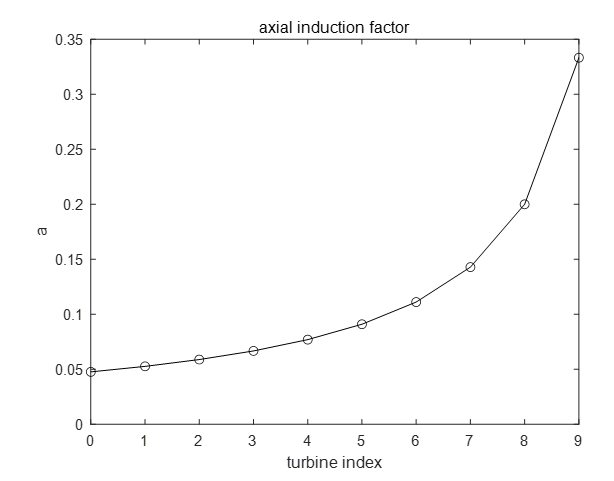
만약 풍력터빈의 개수가 무한대라면 어떻게 될까. 다음 그림은 $N=1000$ 일 때 $P^{greedy}$ 와 $P^{opt}$ 를 그린 것이다. $P^{greedy}$ 의 전력 생산 증가량이 3.85% 인데 비해서 $P^{opt}$ 의 전력 생산 증가량은 235% 에 달한다.

 

 

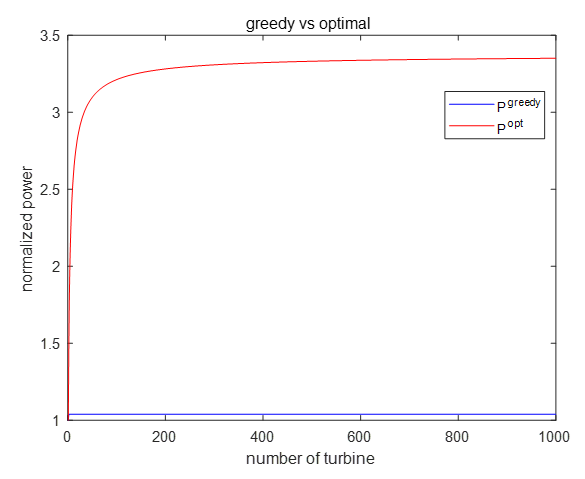
이와 같이 축방향유도제어(AIC)에 의해서 풍력단지의 전력 생산이 증가한 결과는 이상적인 가정하에 아주 간단한 정상상태 매개 변수 모델을 기반으로 얻은 것이다.

하지만 어떤 고충실도 모델을 사용한 연구에 따르면 AIC가 항상 전력 생산을 늘릴 수 있는 것은 아니라고 한다. 사실 AIC에 대한 연구는 상당히 광범위하게 수행되었지만 타당성에 대해서는 아직 결정적인 결과가 없는 실정이다. 비록 AIC로 발전량을 증대시키는 데에는 아직 확신할 수는 없지만, 구조적 하중을 줄일 수는 있고 전력 추종제어에 적용할 수 있다는 연구 결과가 있다.