CR3BP의 무차원화된 운동방정식은 다음과 같았다.
\[ \begin{align} & \ddot{x}-2 \dot{y} - x = - \frac{ (1-\mu)(x+\mu) }{r_{13}^3 } - \frac{ \mu (x+\mu-1) }{ r_{23}^3 } \tag{1} \\ \\ & \ddot{y}+2 \dot{x} - y = - \frac{ (1-\mu) y }{r_{13}^3 } - \frac{ \mu y }{ r_{23}^3 } \\ \\ & \ddot{z} = - \frac{ (1-\mu) z }{r_{13}^3 } - \frac{ \mu z }{ r_{23}^3 } \end{align} \]
여기서
\[ \begin{align} & r_{13}= \sqrt{ (x+\mu)^2+y^2+z^2 } \\ \\ & r_{23}= \sqrt{ (x+\mu-1)^2+y^2+z^2 } \end{align} \]
이다. 위 수식에서 편의상 무차원 변수를 뜻하는 \( \sim \)(tilde)는 모두 제거하였다.
식 (1)에서 주의할 점은 모든 변수와 그 미분은 모두 관성좌표계 \(\{i\}\)가 아니라 관성좌표계에 대해서 일정 각속도로 회전하는 시노딕 좌표계 \(\{b\}\)에서 표현되거나 계산되었다는 점이다. 또한 운동방정식은 두 개의 주요(primary) 질점의 운동이 아니라, 이들의 영향을 받는 작은 질점의 운동방정식이라는 점이다.
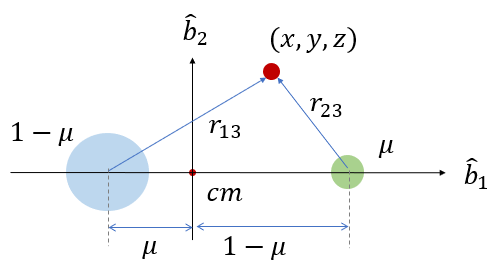
이제 작은 질점이 평형 상태(equilibrium)에 있을 수 있는 점을 계산해 보자. 평형 상태란 질점의 속도와 가속도가 모두 \(0\)인 지점을 말한다. 식 (1)에서 \( \ddot{x}=\ddot{y}=\ddot{z}=0 \), \( \dot{x}=\dot{y}=\dot{z}=0\) 일 때의 위치 \((x_e, y_e, z_e)\)를 계산하면 된다.
\[ \begin{align} & x_e = \frac{ (1-\mu)(x_e+\mu) }{r_{e,13}^3 } + \frac{ \mu (x_e+\mu-1) }{ r_{e,23}^3 } \tag{2} \\ \\ & y_e = \frac{ (1-\mu) y_e }{r_{e,13}^3 } + \frac{ \mu y_e }{ r_{e,23}^3 } \\ \\ & 0 = \frac{ (1-\mu) z_e }{r_{e,13}^3 } + \frac{ \mu z_e }{ r_{e,23}^3 } \end{align} \]
위 식에 의하면 \(z_e=0\) 이므로 평형점은 (\( \hat{b}_1\)-\(\hat{b}_2\)) 평면에 있다는 것은 알 수 있다. 여기서
\[ \begin{align} & r_{e,13}= \sqrt{ (x_e+\mu)^2+y^2_e } \tag{3} \\ \\ & r_{e,23}= \sqrt{ (x_e+\mu-1)^2+y^2_e } \end{align} \]
이다.
이 평형점을 라그랑지 포인트(Lagrange point) 또는 라이브레이션 포인트(libration point)라고 한다.
라그랑지 포인트는 시노딕 좌표계에서 정지해 있지만 관성좌표계에서는 두 개의 주요(primary) 질점과 질점과 동일한 각속도로 회전한다. 라그랑지 포인트는 두 개의 주요(primary) 질점이 가하는 만유인력과 질량중심점으로 향하는 구심력이 정확히 일치하는 지점이기 때문에 작은 질점이 시노딕 좌표계에서 정지해 있을 수 있다. 참고로 코리올리스힘은 평형상태에서는 \(0\)이다.

식 (2)의 해를 구할 전략을 생각해 보자. 우선 라그랑지 포인트는 만유인력과 구심력(또는 반대 방향의 원심력)이 동일한 지점이기 때문에 \(\hat{b}_1\)축상에 있을 수 있다. 이 경우 \(y_e=0\) 이 되고 \(x_e\)는 질점 \(m_1\)과 \(m_2\)사이, 또는 \(m_2\)의 오른쪽, 또는 \(m_1\)의 왼쪽에 위치할 수 있다.

이 경우 평형 상태의 방정식이 비선형이기 때문에 수치적으로 풀어야 한다.
하지만 \(m_1 \gg m_2 \) 또는 \(\mu \ll 1\) 로 가정한다면 각 구간에 해당하는 라그랑지 포인트를 근사적으로 계산할 수 있다.
\[ \begin{align} & \mbox{L1: } \ \ x_e= 1- \left( \frac{\mu}{3(1-\mu)} \right)^{ \frac{1}{3}}, \ \ y_e=0 \\ \\ & \mbox{L2: } \ \ x_e=1-\mu+ \left( \frac{ \mu (1-\mu)^2 }{3} \right)^{ \frac{1}{3} }, \ \ y_e=0 \\ \\ & \mbox{L3: } \ \ x_e= - \left( 1+ \frac{5\mu}{12} \right), \ \ y_e=0 \end{align} \]
여기서 L1은 \(m_1\)과 \(m_2\)사이에 있는 포인트, L2는 \(m_2\)의 오른쪽에 있는 포인트, L3는 \(m_1\)의 왼쪽에 있는 포인트이다.
이 밖에 두 개의 라그랑지 포인트가 더 있다. 식 (3)에서 \(r_{e,13}=r_{e,23}=1\) 이 되도록 \((x_e, y_e)\)를 정하면 식 (2)는 자동으로 만족되는 것을 알 수 있다. 따라서 이 지점도 라그랑지 포인트가 된다. \((x_e, y_e)\)를 계산하면 다음과 같다.
\[ \begin{align} & \mbox{L4: } \ \ x_e= \frac{1}{2} -\mu , \ \ y_e = \frac{\sqrt{3}}{2} \\ \\ & \mbox{L5: } \ \ x_e= \frac{1}{2} -\mu , \ \ y_e = -\frac{\sqrt{3}}{2} \end{align} \]
L4와 L5 포인트는 \(m_1\)과 \(m_2\)를 꼭지점으로 하는 정삼각형의 한 꼭지점에 위치한다.

결론적으로 라그랑지 포인트는 5개가 존재하며 그 위치는 다음과 같다.
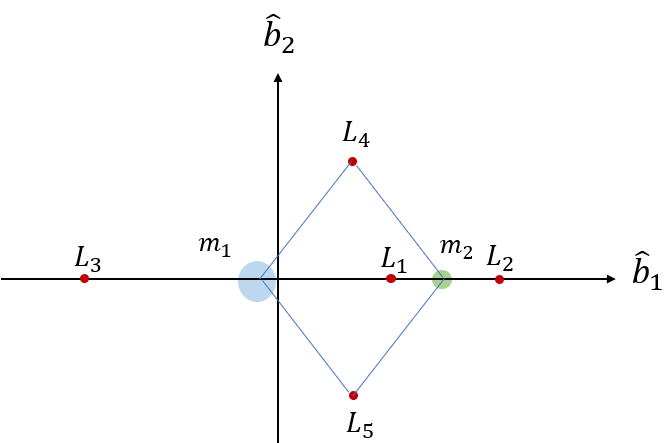
질점 \(m_1\)을 기준으로 5개의 라그랑지 포인트를 그리면 다음과 같다.
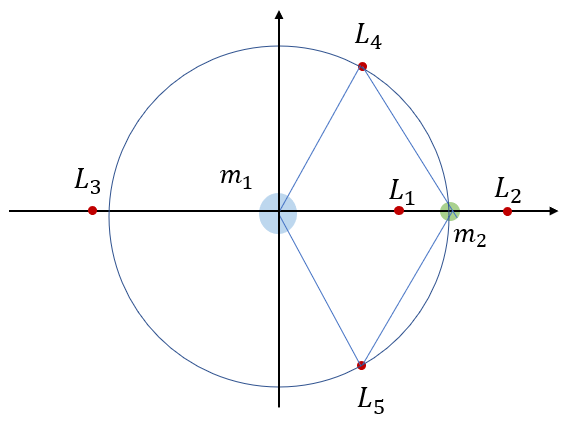
지구-달 시스템에서 라그랑지 포인트를 계산해 보자. 지구의 질량은 \(m_1=5.974 \times 10^{24} \ kg\), 달의 질량은 \(m_2=7.348 \times 10^{22} \ kg\) 이므로, \(\mu=0.0121505\) 이며 라그랑지 포인트는 다음과 같다.
\[ \begin{align} & \mbox{L1: } \ (0.8369626, 0), \ \ \mbox{L2: } \ (1.1556450, 0), \ \ \mbox{L3: } \ (-1.0050627, 0) \\ \\ & \mbox{L4: } \ (0.4878495, 0.8660254), \ \ \mbox{L5: } \ (0.4878495, -0.8660254) \end{align} \]
태양-(지구-달) 시스템의 경우는 태양의 질량이 \(m_1=1.989 \times 10^{30} \ kg\), 지구의 질량이 \(m_2=5.974 \times 10^{24} \ kg\) 이므로, \(\mu =3.03591 \times 10^{-6}\) 이며 라그랑지 포인트는 다음과 같다.
\[ \begin{align} & \mbox{L1: } \ (0.9899961, 0), \ \ \mbox{L2: } \ (1.0100009, 0), \ \ \mbox{L3: } \ (-1.0000013, 0) \\ \\ & \mbox{L4: } \ (0.4999970, 0.8660254), \ \ \mbox{L5: } \ (0.4999970, -0.8660254) \end{align} \]
태양과 행성 및 위성의 물리 데이터는 나사 제트추진연구소(JPL) 사이트에 가면 자세히 볼 수 있다 (https://ssd.jpl.nasa.gov/horizons/).
라그랑지 포인트의 특징과 안정성 문제, 그리고 다른 행성 또는 달을 오가는 궤도 설계에서 라그랑지 포인트가 어떻게 사용되는지 등에 대해서는 다음에 논하기로 한다.
'항공우주 > 우주역학' 카테고리의 다른 글
| 이체문제에서 궤도의 모양 (0) | 2021.12.13 |
|---|---|
| [CR3BP] 자코비 적분 (Jacobi Integral) (0) | 2021.06.16 |
| [CR3BP] 운동방정식의 무차원화 (0) | 2021.04.09 |
| [CR3BP] 운동방정식 유도 (0) | 2021.04.08 |
| 삼체문제 (Three-Body Problem) (0) | 2021.04.07 |




댓글