 tf.reduce_sum 함수
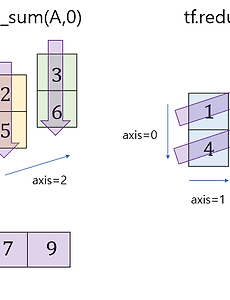
tf.reduce_sum 은 텐서의 모든 성분의 총합을 계산하는 함수다. 예를 들어 다음과 같은 \(2 \times 1 \times 3\) 텐서 \(A\)를 구성하는 모든 성분의 총합을 구하기 위해서 tf.reduce_sum(A) 하면 21 이 나온다. 이 때 모든 차원(dimension)은 사라진다. import tensorflow as tf A = tf.constant([[[1, 2, 3]], [[4, 5, 6]]]) print("A=", A) print(tf.reduce_sum(A)) Output: A= tf.Tensor( [[[1 2 3]] [[4 5 6]]], shape=(2, 1, 3), dtype=int32) tf.Tensor(21, shape=(), dtype=int32) 텐서 \(A\)의..
2021. 3. 12.
tf.reduce_sum 함수
tf.reduce_sum 은 텐서의 모든 성분의 총합을 계산하는 함수다. 예를 들어 다음과 같은 \(2 \times 1 \times 3\) 텐서 \(A\)를 구성하는 모든 성분의 총합을 구하기 위해서 tf.reduce_sum(A) 하면 21 이 나온다. 이 때 모든 차원(dimension)은 사라진다. import tensorflow as tf A = tf.constant([[[1, 2, 3]], [[4, 5, 6]]]) print("A=", A) print(tf.reduce_sum(A)) Output: A= tf.Tensor( [[[1 2 3]] [[4 5 6]]], shape=(2, 1, 3), dtype=int32) tf.Tensor(21, shape=(), dtype=int32) 텐서 \(A\)의..
2021. 3. 12.