탄도 미사일이나 발사체의 추력(thrust)은 로켓 엔진이 연료를 빠르게 분사하면서 생기는 반작용에 의해서 생성된다.
다음 그림은 로켓과 로켓에서 분사된 연료로 구성된 질점(particle) 시스템을 보여주고 있다.
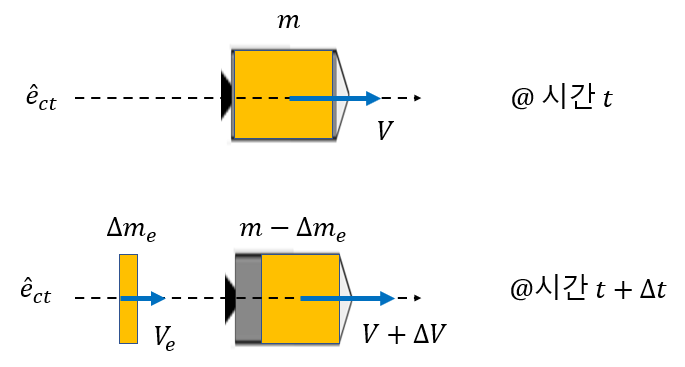
추력 유도 과정을 간단하게 하기 위해서 로켓에는 대기 압력 이외에 다른 힘이 존재하지 않고 분사된 연료의 방향은 로켓 동체의 센터라인과 일치한다고 가정한다. 그림에서 \(\hat{e}_{ct}\)는 로켓 동체의 센터라인을 나타내는 방향 벡터다.
위에 있는 그림은 시간 \(t\)에서 질량 \(m\)인 로켓이 절대 속도 \(V\)로 \(\hat{e}_{ct}\) 방향으로 날아가는 것을 나타내고, 아래 그림은 짧은 시간 \(\Delta t\) 동안에 로켓의 연소과정을 거쳐 적은 질량 \(\Delta m_e\)가 노즐 밖으로 분사되어서 이 영향으로 시간 \(t+\Delta t\)에서 로켓의 질량은 \(\Delta m_e\)만큼 감소하고 속도는 \(\Delta V\)만큼 변화한 것을 나타낸다.
그러면 뉴턴 2법칙에 의해서 전체 시스템의 운동량의 변화는 시스템에 작용한 힘과 같으므로 다음 식이 성립한다.
\[ (m-\Delta m_e )(V+\Delta V) \hat{e}_{ct}+V_e \Delta m_e \hat{e}_{ct}-m V \hat{e}_{ct} = pA_e \Delta t \hat{e}_{ct} \tag{1} \]
여기서 \(p\)는 로켓에 작용하는 대기 압력과 노즐 단면에서의 평균 압력 차이고 \(A_e\)는 노즐 단면적이다.
식 (1)의 양변을 \(\Delta t\)로 나누고 \(\Delta t \to 0\)의 극한을 취하면 다음과 같이 된다.
\[ m \frac{dV}{dt}+(V_e-V) \dot{m}_e = p A_e \tag{2} \]
여기서 \( \dot{m}_e= \frac{dm_e}{dt}\)를 질량 유속(mass flow rate, 양의 값)이라고 한다. 식 (2)는 다음과 같이 쓸 수도 있다.
\[ m \frac{dV}{dt} = V_{rel} \ \dot{m}_e + p A_e \tag{3} \]
여기서 \(V_{rel} = -(V_e-V)\)는 로켓을 기준으로 분사된 질량의 상대속도로서 로켓에서 멀어지는 방향을 플러스(+)로 정한 것이다. 로켓의 질량은 분사되는 질량이 빠져나가므로 시간이 흐름에 따라 다음과 같이 줄어든다.
\[ m = m_0 - \int_{t_0}^t \dot{m}_e \ dt \tag{4} \]
여기서 \(m_0\)는 시간 \(t_0\)에서 로켓의 질량이다.
식 (3)의 오른쪽 항은 가속도 \( \frac{dV}{dt}\)를 일으키는 힘의 불균형을 의미한다. 이 힘이 곧 로켓의 추력 \(T\)이다.
\[ T = V_{rel} \ \dot{m}_e + p A_e \tag{5} \]
\(V_{rel} \ \dot{m}_e\)를 제트 추력이라고 하고, \(pA_e\)를 압력 추력이라고 한다. 위 식은 다음과 같이 쓸 수도 있다.
\[ T = \dot{m}_e \left( V_{rel}+ \frac{pA_e}{ \dot{m}_e} \right) = \dot{m}_e V_{exh} \tag{6} \]
위 식에서 괄호를 유효 배기속도 \(V_{exh}\)라고 한다.
유효 배기속도를 해수면에서의 중력 가속도 \(g_0\)로 나눈 값을 다음과 같이 비추력(specific impulse) \(I_{sp}\)로 정의한다. 비추력의 단위는 시간인 초(sec)다.
\[ I_{sp} = \frac{V_{exh}}{g_0} \tag{7} \]
그러면 추력은 다음과 같이 표현할 수 있다.
\[ T = g_0 I_{sp} \dot{m}_e \tag{8} \]
위 식을 보면 비추력은 \(1 kg\)의 연료가 \(1\)초 동안 연소될 때의 추력을 나타낸다고 할 수 있다. 따라서 비추력이 클수록 연료 효율이 뛰어나다. 하지만 추력은 비추력뿐만 아니라 연료 분사량과 속도의 함수이기도 하다.
고체 로켓의 경우 비추력은 \(200 \sim 300\)초이며, 액체 로켓의 경우 \(250 \sim 450\)초 범위의 값을 갖는다. 이온 엔진의 경우 비추력 값은 \(10^4\)초 보다 크다. 고체 로켓의 경우 비추력은 작지만 대량의 연료를 빠른 속도로 분사할 수 있기 때문에 매우 큰 추력을 생성할 수 있다.
이제 로켓에 대기 압력뿐만 아니라 중력, 항력, 양력이 모두 작용하고 있다고 하자.
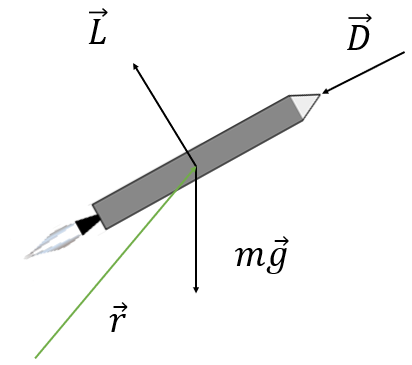
관성 좌표계에서 로켓까지의 위치 벡터를 \( \vec{r}\)이라고 하고 로켓의 질량을 \(m\)이라고 하면, 뉴턴의 운동법칙에 의해서 로켓의 운동 방정식은 다음과 같이 주어진다.
\[ \frac{ ^i d}{dt} (m\vec{v}) = \vec{L}+\vec{D}+m\vec{g} \tag{9} \]
여기서 \(\vec{L}\)은 양력, \(\vec{D}\)는 항력, \(\vec{g}\)는 중력가속도, \(\vec{v}=\frac{^i d\vec{r}}{dt}\)는 속도 벡터, \(m\vec{v}\)는 선형 운동량 벡터다.
추력 방정식 (6)과 운동 방정식 (3)을 이용하면 식 (9)는 다음과 같이 쓸 수 있다.
\[ m \frac{ ^i d\vec{v}}{dt} = \vec{L}+\vec{D}+m\vec{g} + \vec{T} \tag{10} \]
특이한 점은 식 (10)은 질량이 시간의 함수일때의 식이지만, 질량이 상수일 때의 식과 동일하다는 것이다.
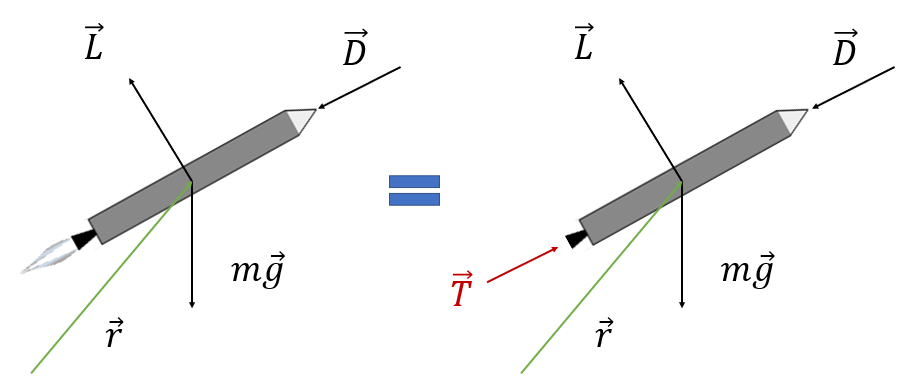
질량이 시간의 함수이라고 해서 식 (9)를 아래 식과 같이 단순하게 미분하면 안된다는 것에 주의해야 한다.
\[ \frac{ ^i d}{dt} (m \vec{v}) \ne \dot{m} \vec{v} + m \frac{^i d \vec{v}}{dt} \tag{11} \]
왜냐하면 식 (9)는 질점에 적용되는 식으로 로켓의 분사와 같이 2개 이상의 질점으로 구성된 질점 시스템의 경우에는 시스템을 구성하는 모든 질점의 운동량의 변화를 고려해야 하기 떄문이다.
'항공우주 > 우주역학' 카테고리의 다른 글
| 더 단순화된 이체문제 (0) | 2021.01.12 |
|---|---|
| 기본 궤도 미분 방정식 (0) | 2021.01.11 |
| 이체문제 (Two-Body Problem) (0) | 2021.01.11 |
| 만유인력의 법칙 (0) | 2021.01.10 |
| 발사체의 발사 궤적 (1) | 2021.01.08 |




댓글