궤도의 비행각과 비행시간

시간 $t=t_0$ 에서 주어진 위치벡터 및 속도벡터를 고전 궤도요소(COE)로 변환하면 궤도의 크기, 모양, 자세에 대해 알 수 있다 (https://pasus.tistory.com/287). 궤도의 크기, 모양, 자세는 ECI좌표계에서 일정하게 유지되고 6개의 궤도요소 중에서 궤도상의 우주비행체의 위치를 나타내는 실제 비행각(true anomaly) $\theta$ 만이 시간의 함수이므로, 우주비행체는 마치 우주공간에 있는 미리 정해진 철로를 따라 운행하는 기차와 같다고 볼 수 있다.

 

 

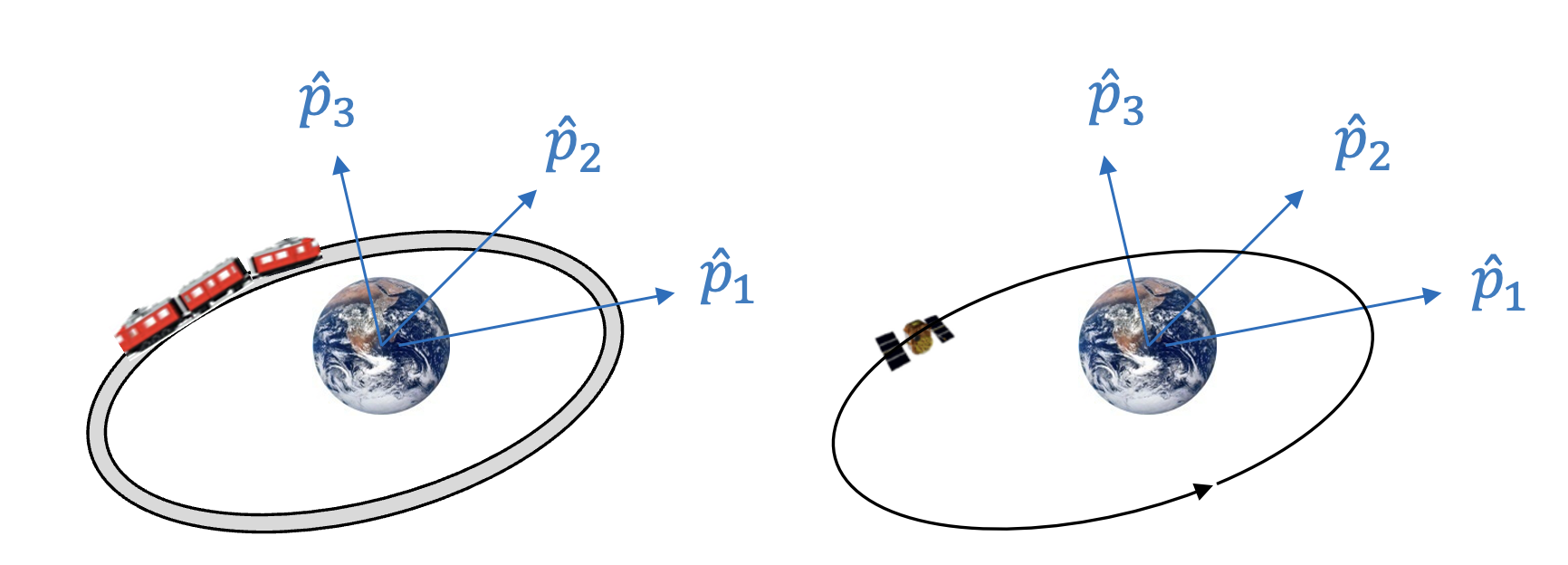
이제 궤도가 주어졌을 때 우주비행체가 궤도상의 한 지점에서 다른 지점까지 비행하는데 걸리는 비행시간(time of flight)을 계산해 보도록 하자.

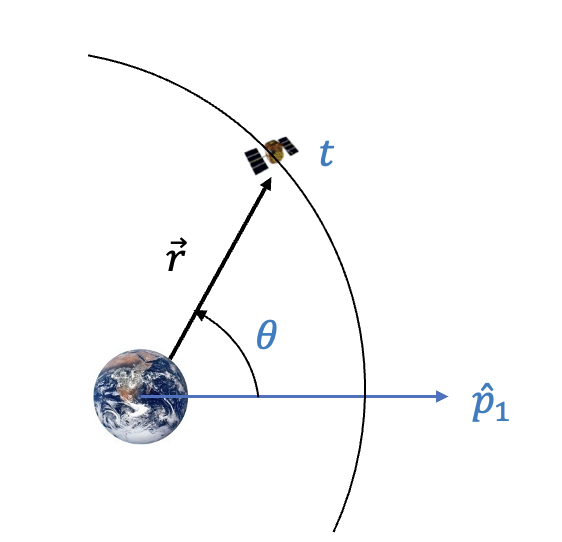
궤도 상에서 우주비행체의 위치는 실제 비행각으로 나타낼 수 있다. 계산은 각운동량의 크기와 실제비행각의 변화율의 관계식으로부터 출발한다 (https://pasus.tistory.com/288).

 

$$\begin{array}{}\text{(1)}& h=r^2\frac{d\theta }{dt}\end{array}$$

 

여기서 $h$ 는 각운동량의 크기고, $r$ 은 지구중심에서 우주비행체까지의 거리로서 다음과 같다.

 

$$\begin{array}{}\text{(2)}& r=\frac{h^2/\mu }{1+e\cos \theta }\end{array}$$

 

여기서 $e$ 는 이심율(eccentricity), $\mu$ 는 중력 파라미터이다. 식 (2)를 (1)에 대입하면 다음과 같이 된다.

 

$$\begin{array}{}\text{(3)}& \frac{{\mu }^2}{h^3}dt=\frac{d\theta }{(1+e\cos \theta {)}^2}\end{array}$$

 

근지점(perigee)에서부터 시간을 측정 한다면, 식 (3)의 적분은 다음과 같다.

 

$$\begin{array}{}\text{(4)}& \frac{{\mu }^2}{h^3}t={\int }_0^{\theta }\frac{d\theta }{(1+e\cos \theta {)}^2}\end{array}$$

 

 

이제 네가지 궤도애 대해서 적분을 풀어보자.

웬궤도는 $e=0$ 이므로 적분이 아주 간단해 진다.

 

$$\begin{array}{}\text{(5)}& \frac{{\mu }^2}{h^3}t={\int }_0^{\theta }d\theta =\theta \end{array}$$

 

원궤도의 반지름과 주기는 각각,

 

$$\begin{array}{}\text{(6)}& r=\frac{h^2}{\mu },T=2\pi \sqrt{\frac{r^3}{\mu }}\end{array}$$

 

이므로(https://pasus.tistory.com/172) 위 식에 대입하면 원궤도에서는 기준점에서 실제 비행각 $\theta$ 까지 비행하는데 걸리는 시간은 다음과 같이 된다.

 

$$\begin{array}{}\text{(7)}& t=\frac{h^3}{{\mu }^2}\theta =\frac{T}{2\pi }\theta \end{array}$$

 

원궤도가 아닌 경우는 식 (4)를 적분해야 하는 복잡한 과정이 필요하다. 다행히 '수학 핸드북'을 찾아보면 식 (4)의 형태를 갖는 함수에 대한 적분 해가 나와 있다.

타원궤도의 경우는 $0<e<1$ 이므로 수학 핸드북에 나와있는 식 (4)의 적분 해를 찾아보면 다음과 같다.

 

$$\begin{array}{r}\text{(8)}& & {\int }_0^{\theta }\frac{d\theta }{(1+e\cos \theta {)}^2}\\ & =\frac{1}{(1-e^2{)}^{3/2}}[2{\tan }^{-1}(\sqrt{\frac{1-e}{1+e}}\tan \frac{\theta }{2})-\frac{e\sqrt{1-e^2}\sin \theta }{1+e\cos \theta }]\end{array}$$

 

여기서 타원의 평균 비행각(mean anomaly)을 다음과 같이 정의하면,

 

$$\begin{array}{}\text{(9)}& M_e=2{\tan }^{-1}(\sqrt{\frac{1-e}{1+e}}\tan \frac{\theta }{2})-\frac{e\sqrt{1-e^2}\sin \theta }{1+e\cos \theta }\end{array}$$

 

식 (8)을 다음과 같이 간단히 표기할 수 있다.

 

$$\begin{array}{}\text{(10)}& \frac{{\mu }^2}{h^3}t=\frac{M_e}{(1-e^2{)}^{3/2}}\end{array}$$

 

따라서, 타원궤도의 근지점에서 실제 비행각 $\theta$ 까지 비행하는데 걸리는 시간은 다음과 같이 된다.

 

$$\begin{array}{}\text{(11)}& t=\frac{h^3}{{\mu }^2}\frac{M_e}{(1-e^2{)}^{3/2}}\end{array}$$

 

타원궤도의 장반경과 주기는 각각 다음과 같이 주어지므로,

 

$$\begin{array}{}\text{(12)}& a=\frac{h^2}{\mu }\frac{1}{1-e^2},T=2\pi \sqrt{\frac{a^3}{\mu }}\end{array}$$

 

식 (11)은 다음과 같이 표현할 수도 있다.

 

$$\begin{array}{}\text{(13)}& t=\frac{T}{2\pi }{M}_e\end{array}$$

 

식 (13)과 식 (7)을 비교해 보면 타원궤도에서 평균 비행각이 원궤도의 실제 비행각과 같은 역할을 하는 것을 알 수 있다.

기하학적으로 식 (9)와 (11)을 도출하는 방법도 있는데 이에 대해서는 추후 논의한다. 케플러는 미적분이 발명되기 80여년전에 기하학적인 방법을 사용하여 케플러 방정식을 유도하였다.

 

 

포물선궤도의 경우는 $e=1$ 이므로 수학 핸드북에 나와있는 식 (4)의 적분 해를 찾아보면 다음과 같다.

 

$$\begin{array}{}\text{(14)}& {\int }_0^{\theta }\frac{d\theta }{(1+\cos \theta {)}^2}=\frac{1}{2}\tan \frac{\theta }{2}+\frac{1}{6}{\tan }^3\frac{\theta }{2}\end{array}$$

 

여기서 포물선궤도의 평균 비행각(mean anomaly)을 다음과 같이 정의하면,

 

$$\begin{array}{}\text{(15)}& M_p=\frac{1}{2}\tan \frac{\theta }{2}+\frac{1}{6}{\tan }^3\frac{\theta }{2}\end{array}$$

 

식 (14)를 다음과 같이 간단히 표기할 수 있다.

 

$$\begin{array}{}\text{(16)}& \frac{{\mu }^2}{h^3}t=M_p\end{array}$$

 

따라서, 포물선궤도의 근지점에서 실제 비행각 $\theta$ 까지 비행하는데 걸리는 시간은 다음과 같이 된다.

 

$$\begin{array}{}\text{(17)}& t=\frac{h^3}{{\mu }^2}{M}_p\end{array}$$

 

쌍곡선궤도의 경우는 $e>1$ 이므로 수학 핸드북에 나와있는 식 (4)의 적분 해는 다음과 같다.

 

$$\begin{array}{r}\text{(18)}& & {\int }_0^{\theta }\frac{d\theta }{(1+e\cos \theta {)}^2}\\ & =\frac{1}{e^2-1}[\frac{e\sin \theta }{1+e\cos \theta }-\frac{1}{\sqrt{e^2-1}}\ln \left(\frac{\sqrt{e+1}+\sqrt{e-1}\tan \frac{\theta }{2}}{\sqrt{e+1}-\sqrt{e-1}\tan \frac{\theta }{2}}\right)]\end{array}$$

 

여기서 쌍곡선궤도의 평균 비행각(mean anomaly)을 다음과 같이 정의하면,

 

$$\begin{array}{}\text{(19)}& M_h=\frac{\sqrt{e^2-1}e\sin \theta }{1+e\cos \theta }-\ln \left(\frac{\sqrt{e+1}+\sqrt{e-1}\tan \frac{\theta }{2}}{\sqrt{e+1}-\sqrt{e-1}\tan \frac{\theta }{2}}\right)\end{array}$$

 

식 (18)을 다음과 같이 간단히 표기할 수 있다.

 

$$\begin{array}{}\text{(20)}& \frac{{\mu }^2}{h^3}t=\frac{M_h}{(e^2-1{)}^{3/2}}\end{array}$$

 

따라서, 쌍곡선궤도의 근지점에서 실제 비행각 $\theta$ 까지 비행하는데 걸리는 시간은 다음과 같이 된다.

 

$$\begin{array}{}\text{(21)}& t=\frac{h^3}{{\mu }^2}\frac{M_h}{(e^2-1{)}^{3/2}}\end{array}$$

 

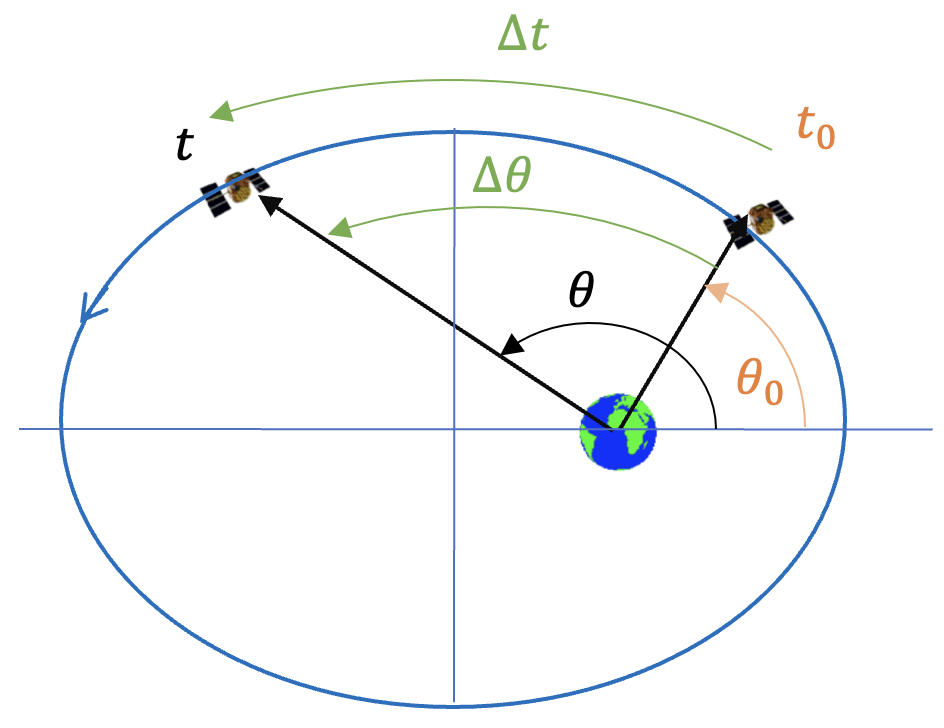
식 (7), (11), (17), (21)의 비행시간은 근지점을 기준으로 한 것이므로, 이를 보다 일반적인 경우로 확장할 필요가 있다. 우주비행체가 근지점이 아닌 지점을 기준으로 할 때는 다음 그림과 같이 비행시간을 구하면 된다.

 

$$\begin{array}{}\text{(22)}& \mathrm{\Delta }t(\mathrm{\Delta }\theta )=t(\theta )-t({\theta }_0)\end{array}$$

 

 

 

식 (11)과 (21)을 보면 타원궤도와 쌍곡선궤도의 수식이 매우 유사하다. 타원궤도 식을 조금 전개하면 다음 식을 얻을 수 있다.

 

$$\begin{array}{r}\text{(23)}& t& =\frac{h^3}{{\mu }^2}\frac{M_e}{{[(-1)(e^2-1)]}^{3/2}}\\ & =\frac{h^3}{{\mu }^2}\frac{M_e}{(j{)}^3(e^2-1{)}^{3/2}}\\ \\ & =\frac{h^3}{{\mu }^2}\frac{j{M}_e}{(e^2-1{)}^{3/2}}\end{array}$$

 

식 (23)과 (21)을 비교해 보면, 타원 식에서 $j{M}_e\to M_h$ 로 치환하면 쌍곡선 식을 얻을 수 있다는 것을 알 수 있다. 이에 대한 자세한 사항은 추후 논의하기로 하겠다.