케플러 문제 (Kepler’s problem) - 1

궤도가 주어졌을 때 우주비행체가 궤도상의 한 지점에서 다른 지점까지 비행하는데 걸리는 비행시간(time of flight)을 함수의 적분 해를 이용하여 계산해 보았다 (https://pasus.tistory.com/307).

하지만 케플러는 미적분이 발명되기 80여년전에 이미 기하학적인 방법을 사용하여 시간 $t=t_0$ 에서의 실제 비행각(true anomaly) ${\theta }_0=\theta (t_0)$ 와 임의의 실제 비행각 $\theta (t)$ 가 주어졌을 때 비행시간 $t-t_0$ 을 계산하였고, 또 역으로 시간 $t=t_0$ 에서의 실제 비행각 ${\theta }_0$ 와 임의의 비행시간 $t-t_0$ 가 주어졌을 때 실제 비행각 $\theta (t)$ 를 구하는 예측문제를 풀었다. 이와 같이 우주비행체의 비행시간과 실제 비행각과의 함수 관계를 다루는 문제를 케플러 문제 (Kepler's problem)라고 한다.

우선 타원궤도에서 케플러 문제를 풀어보고 그 다음 쌍곡선궤도에서도 같은 방법을 적용하여 풀어본다. 케플러 제2법칙인 면적속도 일정의 법칙(https://pasus.tistory.com/172)에 의하면, 다음 그림과 같이 우주비행체가 근지점에서 실제 비행각 $\theta$ 가 만든 면적 $A_1$ 만큼 비행하는데 걸리는 시간 $t$ 는 타원궤도의 전체면적과 주기의 관계식으로 주어진다. 즉,

 

$$\begin{array}{}\text{(1)}& \frac{t}{A_1}=\frac{T}{\pi ab}\end{array}$$

 

여기서 $T$ 는 궤도의 주기이며 $\pi ab$ 는 타원의 면적이다. 따라서 실제 비행각 $\theta$ 가 만든 면적 $A_1$ 을 구할 수 있다면, 비행시간은 쉽게 계산될 수 있다.

면적 $A_1$ 은 다음과 같이 기하학적인 관계에 근거하여 계산할 수 있다. 우선 아래 그림과 같이 타원의 장반경 $a$ 를 반지름으로 하는 가상의 원궤도를 그린다. 그리고 우주비행체의 위치 $B$ 와 장축과 만나는 점 $C$ 를 연결한 선을 연장하여 가상의 원궤도와 만나는 점을 $B^{\prime }$ 이라 한다. 이때 가상의 원궤도 중심 $O$ 에서 $B^{\prime }$ 의 각을 이심 비행각 (eccentric anomaly)이라고 하고 $E$ 라고 표시한다.

 

 

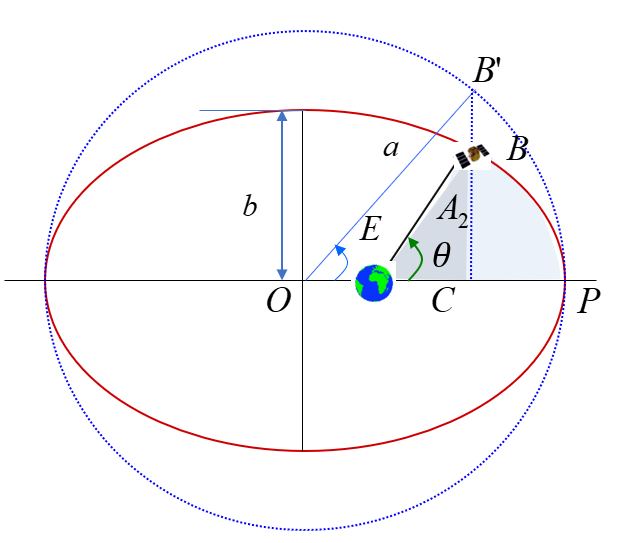
그러면 면적 $A_1$ 은 다음 식으로 계산된다.

 

$$\begin{array}{}\text{(2)}& A_1=A_2+area[PCB]\end{array}$$

 

$area[PCB]$ 는 점 $PCB$ 로 이루어진 도형의 면적이며 타원과 원과의 관계식에 의하여 다음과 같이 표현된다.

 

$$\begin{array}{}\text{(3)}& area[PCB]=area[PC{B}^{\prime }]\frac{b}{a}\end{array}$$

 

$area[PC{B}^{\prime }]$ 는 다음과 같이 주어지므로,

 

$$\begin{array}{}\text{(4)}& area[PC{B}^{\prime }]=\frac{1}{2}{a}^{2}E-\frac{1}{2}{a}^2\cos E\sin E\end{array}$$

 

식(3)과 (4)에 의하여 $area[PCB]$ 는

 

$$\begin{array}{r}\text{(5)}& area[PCB]& =\frac{b}{a}(\frac{1}{2}{a}^{2}E-\frac{1}{2}{a}^2\cos E\sin E)\\ & =\frac{ab}{2}(E-\cos E\sin E)\end{array}$$

 

으로 계산된다. 면적 $A_2$ 는 직각 삼각형이므로 다음과 같이 쉽게 면적을 구할 수 있다.

 

$$\begin{array}{r}\text{(6)}& A_2& =\frac{1}{2}(a\cos E-ae)(a\sin E\frac{b}{a})\\ & =\frac{ab}{2}(\cos E\sin E-e\sin E)\end{array}$$

 

식 (5)와 (6)을 식 (2)에 대입하면 면적 $A_1$ 은

 

$$\begin{array}{}\text{(7)}& A_1=\frac{ab}{2}(E-e\sin E)\end{array}$$

 

이므로 식 (7)을 식 (1)에 대입하면 비행시간 $t$ 를 다음과 같이 계산할 수 있다.

 

$$\begin{array}{}\text{(8)}& t=\sqrt{\frac{a^3}{\mu }}(E-e\sin E)\end{array}$$

 

여기서 타원궤도의 평균 비행각(mean anomaly) $M_e$ 를

 

$$\begin{array}{}\text{(9)}& M_e=E-e\sin E\end{array}$$

 

로 정의하며 이 식을 케플러 방정식 (Kepler's equation)이라고 부른다.

 

 

평균 비행각을 이용하면 비행시간은

 

$$\begin{array}{}\text{(10)}& t=\sqrt{\frac{a^3}{\mu }}{M}_e=\frac{M_e}{n}\end{array}$$

 

이며 $n$ 을 평균 비행각속도 (mean motion)라고 정의한다.

 

$$\begin{array}{}\text{(11)}& n=\sqrt{\frac{\mu }{a^3}}=\frac{2\pi }{T}\end{array}$$

 

식 (10)의 비행시간은 근지점을 기준으로 한 것이다. 우주비행체가 궤도를 여러 번 회전하는 경우와 근지점이 아닌 지점을 기준으로 할 때는 다음과 같이 비행시간을 구해야 한다.

 

$$\begin{array}{r}\text{(12)}& t-t_0& =\frac{2\pi k+M_e-M_{e0}}{n}\\ & =\sqrt{\frac{a^3}{\mu }}(2\pi k+E-e\sin E-E_0+e\sin E_0)\end{array}$$

 

여기서 $k$ 는 우주비행체가 근지점을 통과한 회수이며, $t_0$ 와 $E_0$ 는 우주비행체의 초기 시간과 초기 이심 비행각이다.

식 (12)에서는 우주비행체의 비행시간을 이심 비행각의 함수로 구하였다. 하지만 궤도요소는 실제 비행각의 정보를 주므로 실제 비행각을 이심 비행각으로 변환할 필요가 있다.

다시 위 그림에서 이심 비행각과 실제 비행각과의 관련성을 유도해 내도록 하자. 우선 길이 $\overline{OC}$ 를 기준으로 하면,

 

$$\overline{OC}=a\cos E+r\cos \theta$$

 

가 된다. 따라서

 

$$\begin{array}{r}\text{(13)}& \cos E& =e+\frac{r\cos \theta }{a}\\ & =\frac{e+\cos \theta }{1+e\cos \theta }\end{array}$$

 

이다. 다음으로 길이 $\overline{B^{\prime }C}$ 를 기준으로 하면, 다음식이 성립한다.

 

$$\overline{B^{\prime }C}=a\sin E=\overline{BC}\frac{a}{b}=r\sin \theta \frac{a}{b}$$

 

위 식을 이심 비행각으로 정리하면

 

$$\begin{array}{r}\text{(14)}& \sin E& =\frac{r\sin \theta }{b}\\ & =\frac{\sqrt{1-e^2}\sin \theta }{1+e\cos \theta }\end{array}$$

 

이 된다. 한편 tan 함수의 반각의 공식을 사용하면

 

$$\begin{array}{rl}{\tan }^2\frac{E}{2}& =\frac{1-\cos E}{1+\cos E}\\ \\ & =\frac{(1-e)(1-\cos \theta )}{(1+e)(1+\cos \theta )}\\ \\ & =\frac{(1-e)}{(1+e)}{\tan }^2\frac{\theta }{2}\end{array}$$

 

가 되므로

 

$$\begin{array}{}\text{(15)}& \tan \frac{E}{2}=\sqrt{\frac{1-e}{1+e}}\tan \frac{\theta }{2}\end{array}$$

 

가 됨을 알 수 있다.

식 (9)와 (15)에 의하면 이전 포스트(https://pasus.tistory.com/307)에서 도출했던 타원의 평균 비행각 식 (9)와 완전히 일치함을 알 수 있다.

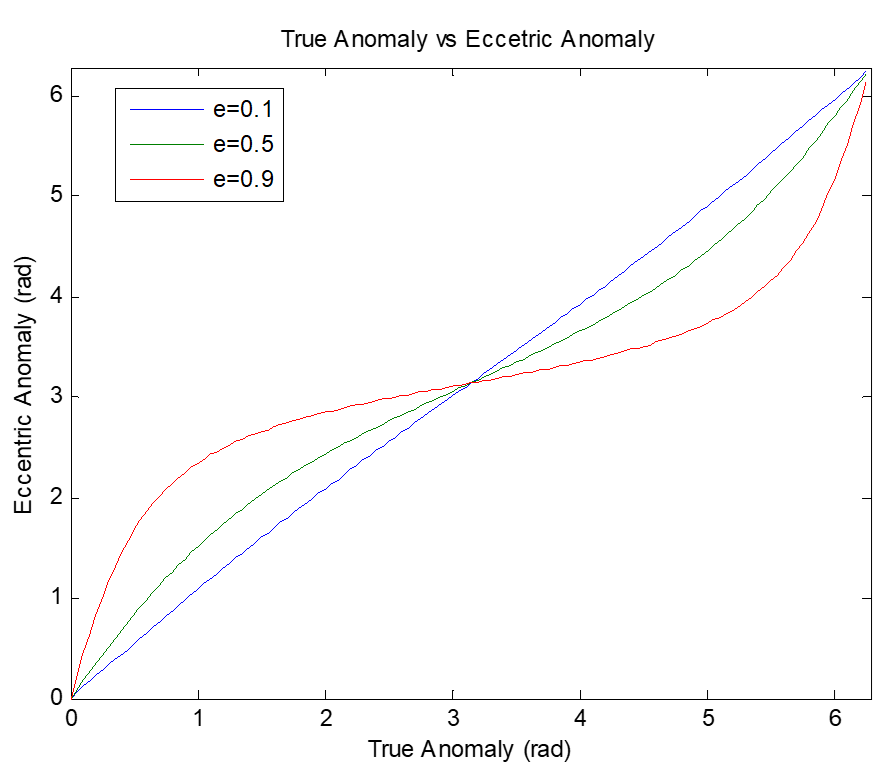
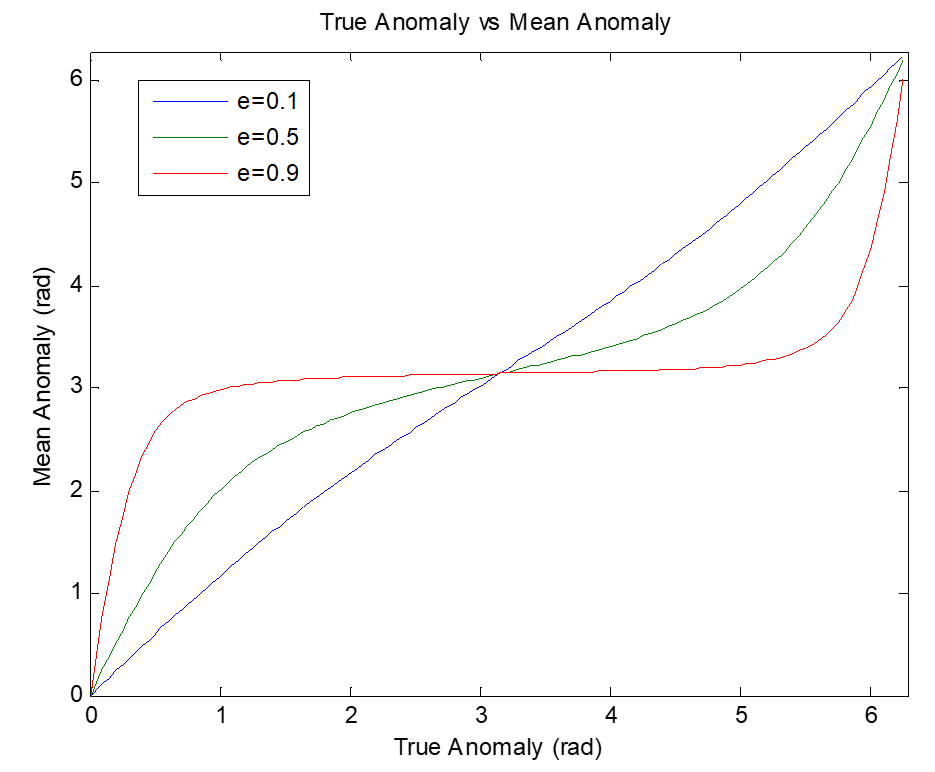
식 (13), (14), (15)는 실제 비행각 $\theta$ 를 이심 비행각 $E$ 로 변환하는 공식이다. 실제 비행각에서 이심 비행각을 계산하거나 또는 이심 비행각에서 실제 비행각을 계산할 때 부호가 문제가 될 수 있는데, 이 경우 평균 비행각, 이심 비행각 및 실제 비행각은 다음 그림과 같이 모두 같은 반구면 ($0^0\sim {180}^0$ 구역과 $-{180}^0\sim 0^0$ 구역) 상에 존재함에 유의하면 된다.