유도항법제어(GNC, guidance, navigation, and control) 분야에서 자세(attitude)란 기준좌표계(reference frame)를 기준으로 3차원 공간에서 항공기 또는 우주비행체 등 운동체에 부착된 동체좌표계(body frame)가 어떤 방향으로 정렬되어 있는 지를 말한다. 자세를 표현하기 위한 방법으로는 오일러각(Euler angles), 방향코사인행렬(DCM, direction cosine matrix), 쿼터니언, 로드리게스 파라미터 등이 있다. 자세를 표현한다 함은 기본적으로 기준좌표계가 동체좌표계와 일치하려면 기준좌표계의 어느 축을 중심으로 얼마만큼 회전해야 하는 지를 나타낸다고 보면 된다.
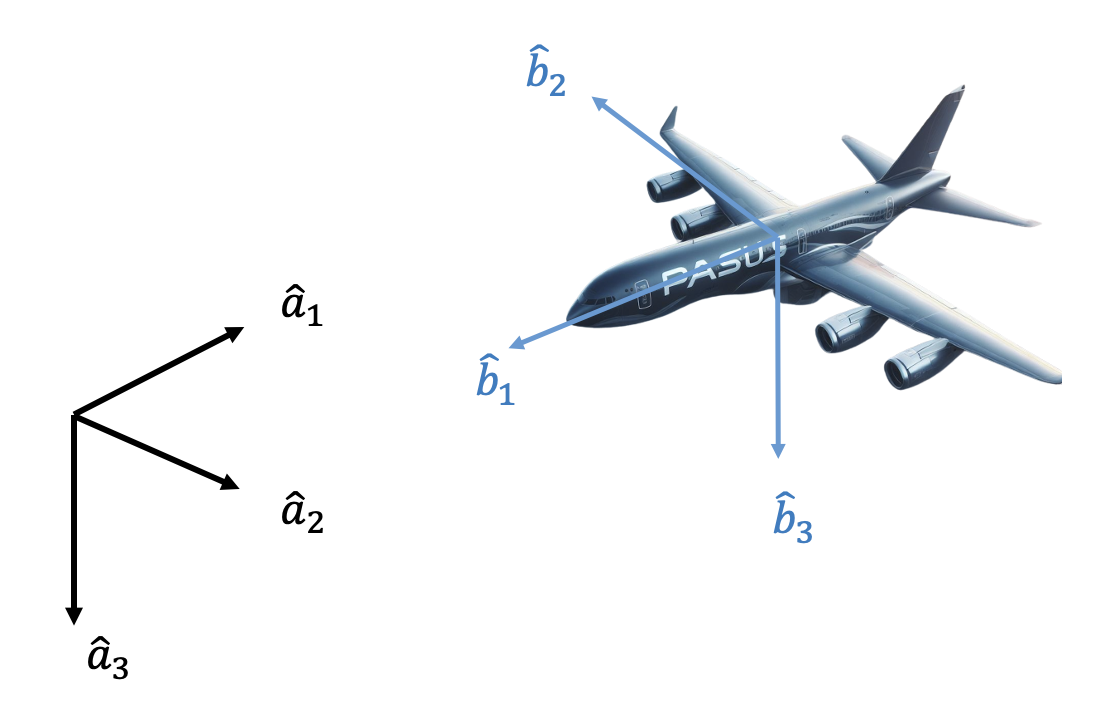
센서의 측정값으로부터 자세를 계산해야 하는데, 이에 관련된 용어가 두 가지가 있다. 바로 자세결정(attitude determination)과 자세추정(attitude estimation)이다. 보통 혼용하는 경우도 있는데 사실 다른 개념이다.
자세결정은 운동체의 자세를 계산하기 위하여 두 개 이상의 벡터 측정을 사용하여 자세를 계산하는 대수적인 방법을 의미한다. 자세결정은 정적(static)인 방법으로서 모든 측정값(measurement)을 동시에 얻거나 또는 측정값을 얻는 동안에 운동체의 움직임을 무시할 수 있을 만큼 시간이 충분히 가까운 조건에서 측정 순간의 자세를 계산한다. 따라서 운동체의 자세나 측정값의 과거 상태에 대한 정보가 필요하지 않다.
반면에 자세추정은 순간적인 측정값이 아니라 과거부터 현재까지 시간에 따른 일련의 측정값을 사용하고 운동체의 움직임도 고려하기 때문에 결과적으로 시간에 의존적인 동적(dynamic)인 방법이다. 또한 운동체의 동역학 모델에서 발생할 수 있는 오류와 측정값에 내재된 노이즈를 고려한 확률론적인 방법을 사용하기 때문에 '결정'이라는 용어보다는 '추정'이라는 용어를 사용한다. 대부분 칼만필터를 이용한다. 문헌에 따라서는 자세추정 대신에 동적 자세결정이라는 용어를 사용하기도 한다.
정적 자세결정에 관한 최초의 알고리즘은 1964년도에 개발된 TRIAD(Tri-Axial Attitude Determination System)로서 두 개의 벡터 측정값을 사용하여 우주비행체의 자세를 계산하는 대수적 방법이었다. 그 후 Wahba가 두 개 이상의 벡터 측정값을 사용하여 자세를 계산하는 최적화 문제로 정립하였다. Davenport는 Wahba의 자세결정 문제를 쿼터니언 기반으로 풀어서 q-method라는 최초의 실용적인 알고리즘을 개발했다. 곧이어 q-방법을 개선한 QUEST(QUaternion Estimator)알고리즘이 개발됐으며 이후로도 Wahba 문제에 대한 또 다른 해로서 SVD(Singular Value Decomposition) 방법과 FOAM(Fast Optimal Attitude Matrix) 알고리즘이 차례로 개발되었다.
구체적인 알고리즘 소개에 앞서서 모든 정적 자세결정 알고리즘에 공통적인 자세결정 원리부터 설명한다.
다음과 같이 어느 2차원 평면에의 고정된 위치에 빨간색 표식이 있다고 하자. 평면상의 모든 위치와 방향은 기준좌표계 \(\{a\}\) 를 기준으로 한다. 평면에 움직이는 로봇이 있다. 로봇에는 동체좌표계 \(\{b\}\) 가 부착되어 있다. 동체좌표계의 x축은 로봇의 전방을 향한다. 로봇은 빨간색 표식을 식별하는 센서를 가지고 있어서 동체좌표계를 기준으로 빨간색 표식의 방향각 \(\alpha\) 를 측정할 수 있다. 방향각은 x축을 기준으로 반시계 방향으로 측정한다.
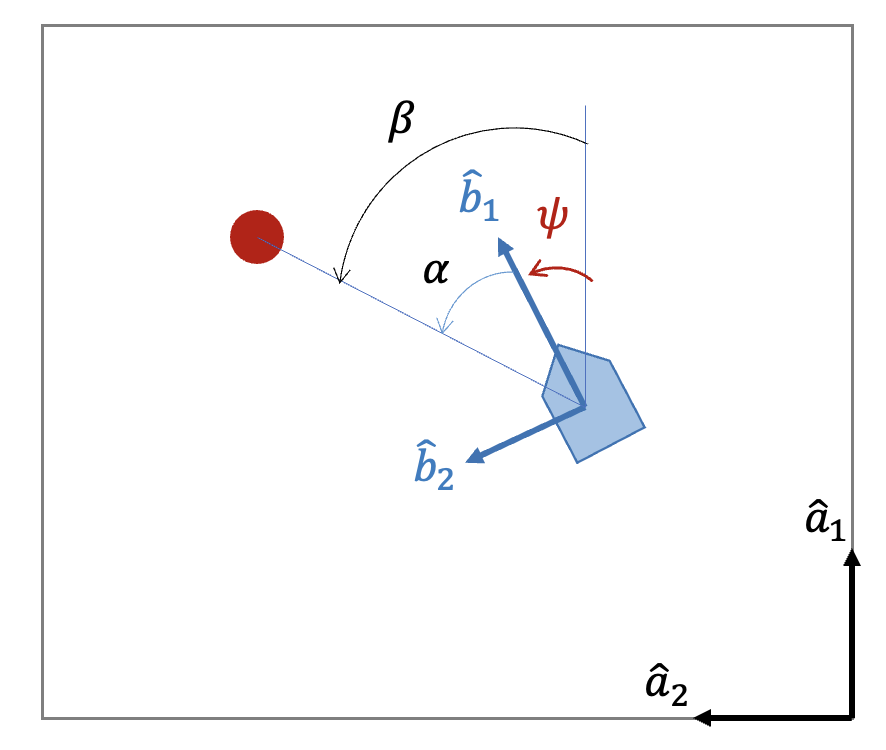
여기서 문제는 기준좌표계를 기준으로 한 로봇 x축의 자세각 \(\psi\) 를 결정할 수 있느냐 이다. 현재 주어진 정보만으로는 자세각 \(\psi\) 를 계산해 낼 수 없다. 하지만 로봇의 현 위치에서 기준좌표계를 기준으로 한 빨간색 표식의 방향각 \(\beta\) 를 알 수만 있다면 \(\psi =\beta -\alpha\) 로 계산 가능하다. 즉 로봇의 현 위치에서 기준좌표계를 기준으로 한 방향각과 로봇의 동체좌표계를 기준으로 한 방향각이 주어진다면 기준좌표계를 기준으로 한 로봇의 자세각을 결정할 수 있다.
그렇다면 로봇의 현 위치에서 기준좌표계를 기준으로 한 방향각은 어떻게 알 수 있을까. 기준좌표계 \(\{a\}\) 에 대해서 빨간색 표식은 고정되어 있기 때문에 또는 위치 좌표를 알 수 있기 때뮨에 만약 기준좌표계에 대한 로봇의 현 위치 좌표를 알 수 있다면 방향각 \(\beta\) 를 계산해 낼 수 있다. 이를 '수학모델'에 의한 측정값이라고 한다. 즉 동체좌표계를 기준으로 한 센서의 방향각 측정값과 기준좌표계를 기준으로 한 '수학모델'의 방향각 측정값이 주어지면, 기준좌표계를 기준으로 하는 로봇의 자세각을 결정할 수 있다. 이것이 정적 자세결정의 원리이다.
다만 2차원 평면과 달리 3차원 공간에서는 운동체의 자세를 결정하기 위해서 빨간색 표식에 해당하는 기준점이 2개 이상 필요하다.
여기에서는 우선 TRIAD 알고리즘을 소개하기로 한다. 이 후 Wahba 문제를 비롯한 다른 정적 자세결정 알고리즘도 차차 소개하기로 하겠다.
TRIAD는 개발 이래 약 20여년 동안 대표적인 자세결정 방법으로 각광받았다. TRIAD는 매 순간마다 두 개의 단위벡터 측정이 가능하고 이 두 벡터는 동일한 방향을 가리키면 안된다는 가정을 전제로 한다. 우주비행체의 자세결정 문제에서 일반적으로 사용하는 두 벡터는 태양센서와 자기장센서가 각각 태양과 지구 자기장 방향을 가리키는 단위벡터이거나, 두 개의 별센서가 서로 다른 항성을 가리키는 단위벡터이다.
두 단위벡터를 각각 \(\hat{s}, \ \hat{m}\) 이라고 표기하자. 그리고 두 단위벡터를 기준좌표계 \(\{a\}\) 와 동체좌표계 \(\{b\}\) 로 표현한 벡터를 각각 \(\mathbf{s}^a, \ \mathbf{s}^b\) 와 \(\mathbf{m}^a, \ \mathbf{m}^b\) 로 표기한다. 그러면 좌표계 \(\{a\}\) 와 \(\{b\}\) 의 DCM \(C_b^a\) 를 이용하여 두 벡터의 관계식을 다음과 같이 쓸 수 있다.
\[ \begin{align} \mathbf{s}^a &=C_b^a \mathbf{s}^b \tag{1} \\ \\ \mathbf{m}^a &=C_b^a \mathbf{m}^b \end{align} \]
여기서 \(\mathbf{s}^b\) 와 \(\mathbf{m}^b\) 는 각각 운동체에 부착된 센서로 측정한 단위벡터이고, \(\mathbf{s}^a\) 와 \(\mathbf{m}^a\) 는 각각 기준좌표계에서 '수학모델'로 계산된 단위벡터이다. TRIAD 알고리즘은 식 (1)에 있는 두 개의 식으로부터 운동체의 자세인 DCM \(C_b^a\) 를 계산하는 방법을 제공해 준다.
식 (1)에서 2개의 식이 필요한 이유는 단위벡터는 2자유도, DCM은 3자유도를 갖기 때문이다.

방향코사인행렬, 오일러각, 그리고 쿼터니언 | 박성수 | 딥웨이브- 교보ebook
이 책에서는 방향코사인행렬, 오일러각, 쿼터니언과 이들의 시간 변화율에 대해서 공부합니다. 모두 3차원 공간 상에서 어떤 기준 좌표계에 대해서 운동하는 강체의 상대적인 자세의 변화를 표
ebook-product.kyobobook.co.kr
\(C_b^a\) 를 계산하기 위하여 먼저 중간단계 좌표계인 \(\{t\}\) 를 도입한다. 좌표계 \(\{t\}\) 의 \(\hat{t}_1\) 축은 \(\hat{s}\) 로 선택한다.
\[ \begin{align} & \hat{s}= \hat{t}_1 \tag{2} \\ \\ \to \ & \mathbf{t}_1^a= \mathbf{s}^a, \ \ \ \ \ \mathbf{t}_1^b=\mathbf{s}^b \end{align} \]
그리고 \(\hat{t}_2\) 축을 다음과 같이 정의한다.
\[ \begin{align} & \hat{t}_2= \frac{\hat{s} \times \hat{m}}{|\hat{s} \times \hat{m} |} \tag{3} \\ \\ \to \ & \mathbf{t}_2^a= \frac{ \left[ \mathbf{t}_1^a \times \right] \mathbf{m}^a}{\vert \left[ \mathbf{t}_1^a \times \right] \mathbf{m}^a \vert} , \ \ \ \ \ \mathbf{t}_2^b= \frac{ \left[ \mathbf{t}_1^b \times \right] \mathbf{m}^b}{\vert \left[ \mathbf{t}_1^b \times \right] \mathbf{m}^b \vert } \end{align} \]
그러면 오른손 법칙에 의해서 \(\hat{t}_3\) 축은 자동적으로 다음과 같이 정해진다.
\[ \begin{align} & \hat{t}_3= \hat{t}_1 \times \hat{t}_2 \tag{4} \\ \\ \to \ & \mathbf{t}_3^a= \left[ \mathbf{t}_1^a \times \right] \mathbf{t}_2^a, \ \ \ \ \ \mathbf{t}_3^b=\left[ \mathbf{t}_1^b \times \right] \mathbf{t}_2^b \end{align} \]
식 (2), (3), (4)에서 구한 \(\mathbf{t}_1^a, \ \mathbf{t}_2^a, \ \mathbf{t}_3^a\) 와 \(\mathbf{t}_1^b, \ \mathbf{t}_2^b, \ \mathbf{t}_3^b\) 를 이용하면 좌표계 \(\{a\}\) 에서 \(\{t\}\) 로의 DCM과 좌표계 \(\{b\}\) 에서 \(\{t\}\) 로의 DCM을 다음과 같이 계산할 수 있다.
\[ \begin{align} C_t^a & = \begin{bmatrix} \hat{a}_1 \cdot \hat{t}_1 & \hat{a}_1 \cdot \hat{t}_2 & \hat{a}_1 \cdot \hat{t}_3 \\ \hat{a}_2 \cdot \hat{t}_1 & \hat{a}_2 \cdot \hat{t}_2 & \hat{a}_2 \cdot \hat{t}_3 \\ \hat{a}_3 \cdot \hat{t}_1 & \hat{a}_3 \cdot \hat{t}_2 & \hat{a}_3 \cdot \hat{t}_3 \end{bmatrix} = \begin{bmatrix} \mathbf{t}_1^a & \mathbf{t}_2^a & \mathbf{t}_3^a \end{bmatrix} \tag{5} \\ \\ C_t^b &=\begin{bmatrix} \hat{b}_1 \cdot \hat{t}_1 & \hat{b}_1 \cdot \hat{t}_2 & \hat{b}_1 \cdot \hat{t}_3 \\ \hat{b}_2 \cdot \hat{t}_1 & \hat{b}_2 \cdot \hat{t}_2 & \hat{b}_2 \cdot \hat{t}_3 \\ \hat{b}_3 \cdot \hat{t}_1 & \hat{b}_3 \cdot \hat{t}_2 & \hat{b}_3 \cdot \hat{t}_3 \end{bmatrix} = \begin{bmatrix} \mathbf{t}_1^b & \mathbf{t}_2^b & \mathbf{t}_3^b \end{bmatrix} \tag{6} \end{align} \]
그러면 식 (5)와 (6)을 이용해서 좌표계 \(\{a\}\) 에서 \(\{b\}\) 로의 DCM \(C_b^a\) 는 다음 식으로 계산할 수 있다.
\[ C_b^a=C_t^a C_b^t=C_t^a (C_t^b )^T \tag{7} \]
예를 들어본다. 먼저 기준좌표계 \(\{a\}\) 에서 단위벡터 \(\hat{s}, \ \hat{m}\) 이 다음과 같이 주어졌다고 하자.
\[ \mathbf{s}^a= \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \ \ \ \ \ \mathbf{m}^a= \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \tag{8} \]
좌표계 \(\{a\}\) 에서 \(\{b\}\) 로의 참값 DCM은 3-2-1 오일러각 30도, 20도, 10도 회전을 통해서 다음과 같다고 하자.
\[ C_b^a= \begin{bmatrix} 0.9254 & 0.0180 & 0.3785 \\ 0.1632 & 0.8826 & -0.4410 \\ -0.3420 & 0.4698 & 0.8138 \end{bmatrix} \tag{9} \]
그러면 동체좌표계 \(\{b\}\) 에서 단위벡터 \(\hat{s}, \ \hat{m}\) 은 다음과 같다.
\[ \mathbf{s}^b= \begin{bmatrix} 0.9254 \\ 0.0180 \\ 0.3785 \end{bmatrix}, \ \ \ \ \ \mathbf{m}^b= \begin{bmatrix} -0.3420 \\ 0.4698 \\ 0.8138 \end{bmatrix} \tag{10} \]
이제 식 (8)과 (10)을 측정 단위벡터로 간주하고 TRIAD 알고리즘을 사용하여 DCM \(C_b^a\) 를 계산해보자. 먼저 식 (2)에 의해서 좌표계 \(\{t\}\) 의 \(\hat{t}_1\) 축은 다음과 같다.
\[ \mathbf{t}_1^a= \mathbf{s}^a= \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \ \ \ \ \ \mathbf{t}_1^b= \mathbf{s}^b = \begin{bmatrix} 0.9254 \\ 0.0180 \\ 0.3785 \end{bmatrix} \]
식 (3)에 의해서 \(\hat{t}_2\) 축은 다음과 같다.
\[ \mathbf{t}_2^a= \begin{bmatrix} 0 \\ -1 \\ 0 \end{bmatrix}, \ \ \ \ \ \mathbf{t}_2^b= \begin{bmatrix} -0.1632 \\ -0.8826 \\ 0.4410 \end{bmatrix} \]
식 (4)의해서 \(\hat{t}_3\) 축은 다음과 같다.
\[ \mathbf{t}_3^a= \begin{bmatrix} 0 \\ 0 \\ -1 \end{bmatrix}, \ \ \ \ \ \mathbf{t}_3^b= \begin{bmatrix} 0.3420 \\ -0.4698 \\ -0.8138 \end{bmatrix} \]
식 (5), (6), (7)에 의해서 DCM은 다음과 같이 계산되어서 식 (9)로 주어지는 참값 DCM과 일치함을 알 수 있다.
\[ C_b^a= \begin{bmatrix} 0.9254 & 0.0180 & 0.3785 \\ 0.1632 & 0.8826 & -0.4410 \\ -0.3420 & 0.4698 & 0.8138 \end{bmatrix} \]
다음은 TRIAD 알고리즘을 매트랩 코드로 작성한 것이다.
function Cab = triad(s_a, s_b, m_a, m_b)
% TRIAD static attitide determination
% input:
% s_a, s_b of s_hat in frame {a} and {b}
% m_a, m_b of m_hat in frame {a} and {b}
% output:
% DCM C^a_b
%
% coded by st.watermelon
% t1-axis
t1_a = s_a;
t1_b = s_b;
% t2-axis
t1_ax = [0 -t1_a(3) t1_a(2);
t1_a(3) 0 -t1_a(1);
-t1_a(2) t1_a(1) 0];
t1_bx = [0 -t1_b(3) t1_b(2);
t1_b(3) 0 -t1_b(1);
-t1_b(2) t1_b(1) 0];
t2_a = t1_ax*m_a;
t2_a = t2_a /sqrt(t2_a'*t2_a);
t2_b = t1_bx*m_b;
t2_b = t2_b /sqrt(t2_b'*t2_b);
% t3-axis
t3_a = t1_ax*t2_a;
t3_b = t1_bx*t2_b;
% C^a_t and C^b_t
Cat = [t1_a t2_a t3_a];
Cbt = [t1_b t2_b t3_b];
% result
Cab = Cat*(Cbt)';
'항공우주 > 우주역학' 카테고리의 다른 글
| 정적 자세결정: QUEST (0) | 2023.11.01 |
|---|---|
| 정적 자세결정: Davenport의 q-방법 (0) | 2023.10.22 |
| [CR3BP] 주기궤도의 매니폴드 계산 (0) | 2023.08.01 |
| 궤도요소 (COE)로 부터 위치 및 속도벡터 계산 (0) | 2023.07.31 |
| 궤도요소 (COE) 계산 (0) | 2023.07.26 |




댓글