연속시간 최적제어에 사용되는 두 가지 유형의 수치적 방법 중 직접방법(direct method)은 최적제어 문제에서 상태변수와 제어입력을 이산화(discretization)시켜 비선형 프로그래밍 문제(NLP, nonlinear programming problem)로 바꾸는 것이다.
유사 스펙트럴 방법(pseudospectral method)은 지난 10여년 동안 최적제어 분야에서 널리 사용된 직접방법 중의 하나로서 콜로케이션 포인트(collocation point)와 보간점(interpolating point)을 이용하는 것이 핵심이다.
지금까지 살펴본 수학적 배경지식인 라그랑지 보간 다항식, 가우시안 쿼드래처, 유사 스펙트럴 방법 등을 간략히 요약한 다음에 연속시간 최적제어 문제를 비선형 프로그래밍 문제로 변환해 보기로 한다.
라그랑지 보간 다항식(Lagrange interpolation polynomials)은 임의의 점(보간점)에서 어떤 함수의 값이 주어졌을 때, 그 점들을 모두 지나는 근사 함수를 라그랑지 기저 다항식(Lagrange basis polynomial)의 조합으로 표현한 것이다(https://pasus.tistory.com/177).
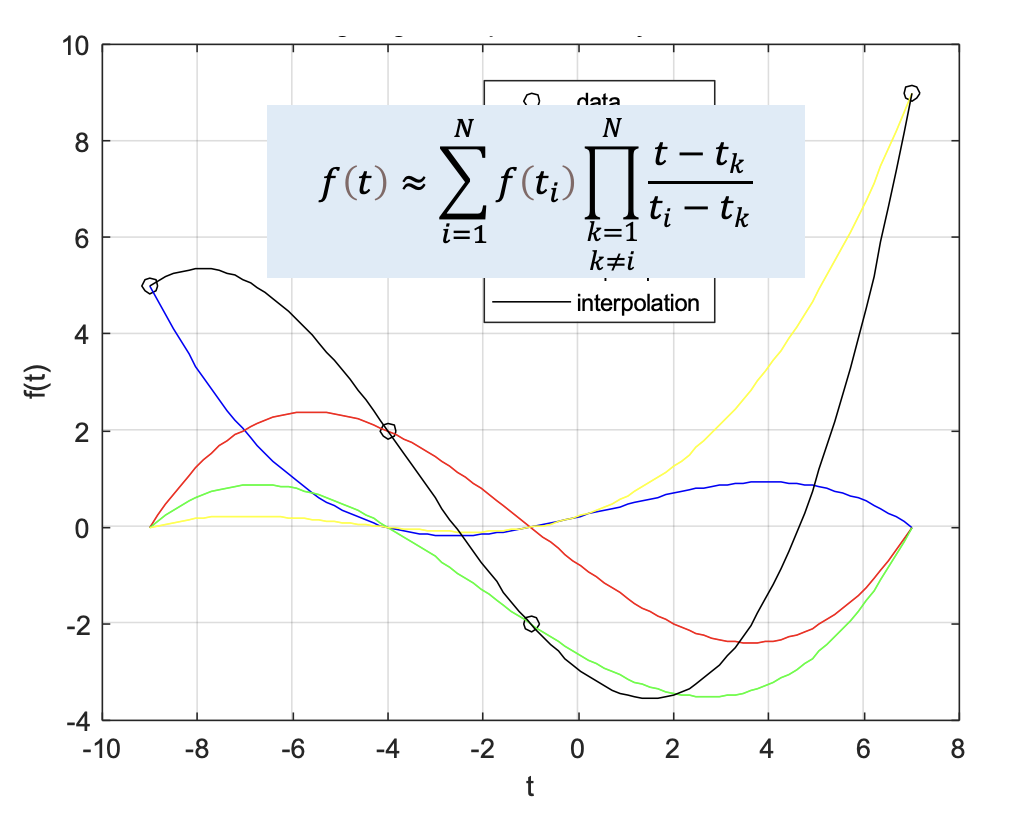
가우시안 쿼드래처(Gaussian quadrature)는 어떤 함수의 적분값을 적분 구간내의 특정 지점(쿼드래처 포인트)에서의 함수값의 가중치 합으로 계산하는 수치적분 방법이다(https://pasus.tistory.com/178).
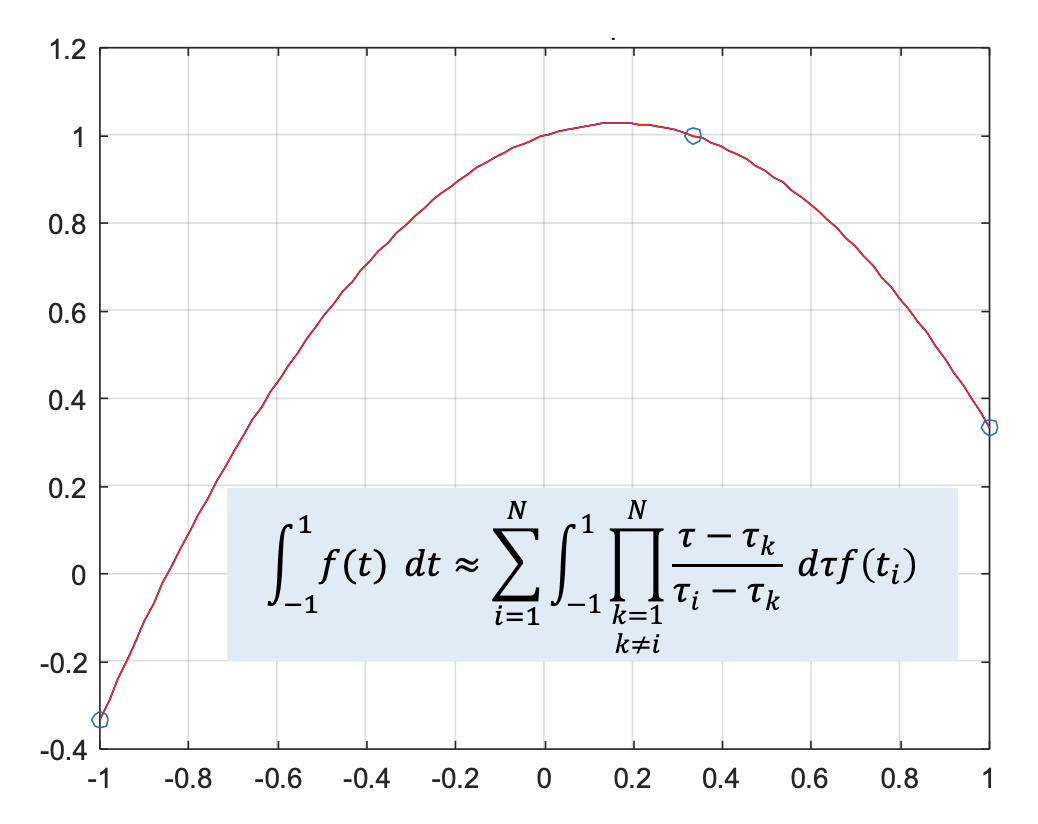
유사 스펙트럴 방법은 경계조건을 갖는 미분방정식의 근사해를 구하는 방법으로서 트라이얼 함수로 라그랑지 기저 다항식을 사용하고 콜로케이션 포인트에서 미분방정식을 정확히 만족시키는 방법이다 (https://pasus.tistory.com/202).
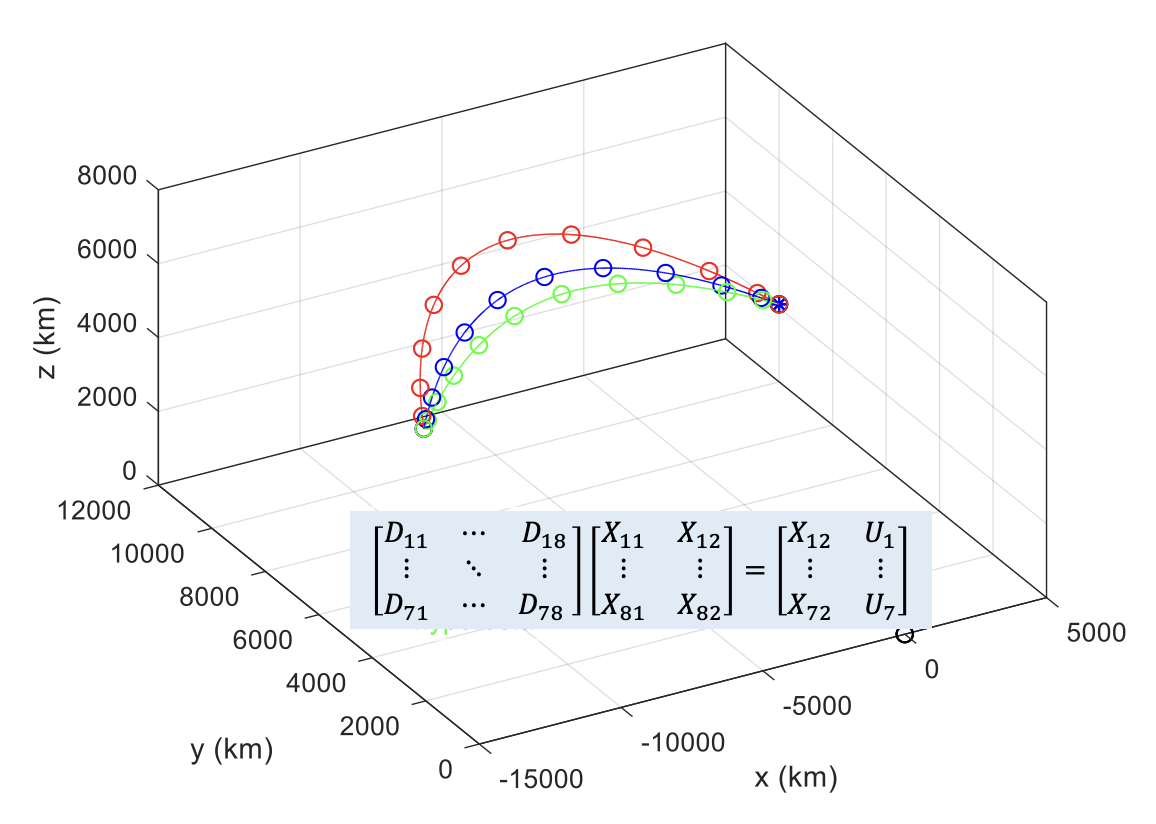
콜로케이션 포인트는 LGL, LG, LGR 포인트 등이 사용된다(https://pasus.tistory.com/176). 보간점은 라그랑지 기저 다항식의 직교(orthogonality) 특성을 이용하기 위해서 콜로케이션 포인트와 일치시키며 경계조건에 따라서 콜로케이션 포인트 외에 더 추가될 수 있다. 따라서 보간점의 갯수는 콜로케이션 포인트의 갯수보다 같거나 많다.
이제 연속시간 최적제어 문제를 수학식으로 표현하면 다음과 같다. 우선 시스템의 동역학은 다음과 같이 미분방정식으로 표현된다.
\[ \dot{\mathbf{x}}(t)= \mathbf{f}( \mathbf{x}(t), \mathbf{u}(t), t) \tag{1} \]
여기서 \(\mathbf{x}(t) \in \mathbb{R}^n\) 는 상태변수 벡터, \(\mathbf{u}(t) \in \mathbb{R}^p\) 는 제어변수 벡터이고 \(t\) 는 연속시간(continuous-time)을 의미한다. 제어변수가 최소화해야 할 목적함수는 다음과 같이 주어진다.
\[ J=\phi(\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f )+ \int_{t_0}^{t_f} g(\mathbf{x}(t), \mathbf{u}(t), t) \ dt \tag{2} \]
여기서 \(t_0\) 는 초기시간(initial time), \(t_f\) 는 최종시간(final time)이며, \(g(\mathbf{x}(t), \mathbf{u}(t), t)\) 는 운행비용(running cost), \(\phi(\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f )\) 는 초기시간과 최종시간에서의 비용이다. 초기 및 최종 상태변수 제약조건은 상태변수의 초기값과 최종값의 함수로서 다음과 같이 주어진다.
\[ \psi (\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f )=0 \tag{3} \]
여기서 \(\psi \in \mathbb{R}^m\) 로서 구성요소가 \(m\) 개인 벡터다. 경로 제약조건(path constraint)은 상태변수와 제어변수의 함수로서 시스템의 경로에 가해지는 제약조건을 다음과 같이 부등식으로 나타낸다.
\[ \mathbf{C}( \mathbf{x}(t), \mathbf{u}(t), t) \le 0 \tag{4} \]
최적제어 문제는 동역학, 상태변수 제약조건, 경로 제약조건을 만족하면서 목적함수를 최소화시키는 제어변수 \(\mathbf{u}(t), \ t \in [t_0, t_f]\) 를 구하는 것이다. 식 (1)~(4)로 주어지는 최적제어 문제의 형식을 볼자(Bolza) 형식이라고 한다.
최적제어 문제에 유사 스펙트럴 방법을 적용하고자 하는 이유는 동적 최적화(dynamic optimization) 문제를 효율적으로 비선형 프로그래밍 문제(NLP) 문제로 바꿀 수 있기 때문이다. NLP 문제는 다양한 솔루션과 알고리즘이 존재하므로 이를 이용하겠다는 것이다. 이에 대한 기본 아이디어는 다음과 같다.
1. 시스템 방정식 (1)은 미분방정식이므로 상태변수를 라그랑지 보간 다항식으로 근사화한다. 그리고 콜로케이션 포인트에서 미분방정식을 배치하여 동역학을 충족시킨다. 그러면 보간점에서는 상태변수가 이산화되고 콜로케이션 포인트에서는 제어입력이 이산화 된다.
2. 목적함수 (2)는 적분을 포함하므로, 가우시안 쿼드래처를 이용하여 근사화 한다. 쿼드래처 포인트는 콜로케이션 포인트와 동일하게 선정한다.
3. 경계조건 (3)은 \(t_0\) 와 \(t_f\) 에서 이산화된 점(보간점 또는 경계조건을 만족시키기 위해서 더 추가된 점)에서 만족시킨다. 경로제약 조건 (4)는 모든 콜로케이션 포인트에서 만족시킨다.
변환이 끝나면 최적제어 문제는 여러 개의 대수방정식 제약조건을 갖는 비선형 프로그래밍 문제로 바뀌게 된다.
유사 스펙트럴 방법을 적용하기 위해서는 우선 시간구간 \(t \in [t_0, t_f]\) 를 표준 시간구간인 \(\tau \in [-1, 1]\) 로 변경해야 한다.

다음과 같은 시간 변환 관계식을 이용하여
\[ t=\frac{t_f-t_0}{2} \tau+ \frac{t_f+t_0}{2} \tag{5} \]
시스템 방정식, 경계조건, 경로제약 조건, 목적함수를 각각 다음과 같이 변환시킨다.
\[ \begin{align} & \frac{d \mathbf{x} (\tau)}{d \tau} = \frac{(t_f-t_0 )}{2} \mathbf{f}( \mathbf{x}( \tau), \mathbf{u}(\tau), \tau, t_0, t_f ) \tag{6} \\ \\ & J= \phi( \mathbf{x}(-1), \mathbf{x}(1), t_0, t_f )+ \frac{(t_f-t_0 )}{2} \int_{-1}^1 g( \mathbf{x}(\tau), \mathbf{u}( \tau), \tau ,t_0, t_f) \ d \tau \\ \\ & \psi ( \mathbf{x}(-1), \mathbf{x}(1), t_0, t_f )=0 \\ \\ & \frac{(t_f-t_0 )}{2} \mathbf{C}( \mathbf{x} (\tau), \mathbf{u} (\tau), \tau, t_0, t_f ) \le 0 \end{align} \]
유사 스펙트럴 방법은 콜로케이션 포인트를 기준으로 로바토(Labatto), 라다우(Radau), 가우스(Gauss) 유사 스펙트럴 방법으로 분류할 수 있다. 세 방법의 콜로케이션 포인트는 동일한 시간 범위 \([-1, 1]\) 에서 정의되지만 포인트의 위치는 서로 다르다.
다음 포스팅에서는 각각의 방법에 대해서 살펴보기로 하자. 그 전에 동등한 비교를 위해서 최적제어 문제 예제를 먼저 풀어본다. 대부분의 최적제어 문제는 복잡해서 해석적인 해를 얻을 수 있는 경우가 드물지만 이 예제는 해석적인 해가 존재하고 간단하기 때문에 최적제어를 정적 파라미터 최적화 문제로 변환되는 과정을 자세히 살펴 볼 수 있을 뿐만 아니라 정확도도 비교해 볼 수 있다.
다음과 같은 시스템이 있다.
\[ \begin{align} \dot{x}_1 &= x_2 \\ \\ \dot{x}_2 &=u \end{align} \]
(a) \(t=0\) 과 \(t=2\) 에서의 조건이 다음과 같을 때,
\[ \begin{bmatrix} x_1 (0) \\ x_2 (0) \end{bmatrix}= \begin{bmatrix} 2 \\ 1 \end{bmatrix}, \ \ \ \ \ \begin{bmatrix} x_1 (2) \\ x_2 (2) \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \end{bmatrix} \]
다음 목적함수
\[ J_1= \frac{1}{2} \int_0^2 u^2 (t) \ dt \]
를 최소화하는 최적제어는 다음과 같다.
\[ \begin{align} u(t) &=4.5t-5 \\ \\ x_1 (t) &=0.75t^3-2.5t^2+t+2 \\ \\ x_2 (t) &=2.25t^2-5t+1 \end{align} \]

(b) \(t=0\) 에서의 조건이 \(x_1 (0)=2, \ x_2 (0)=1\) 이고, \(t=2\) 에서는 조건이 지정되지 않았을 때, 다음 목적함수
\[ J_2= \frac{1}{2} \left( x_1^2 (2)+x_2^2 (2) \right)+ \frac{1}{2} \int_0^2 u^2 (t) \ dt \]
를 최소화하는 최적제어는 다음과 같다.
\[ \begin{align} u(t) &= 1.43t-2.24 \\ \\ x_1 (t) &=0.24t^3-1.12t^2+t+2 \\ \\ x_2 (t) &=0.72t^2-2.24t+1 \end{align} \]
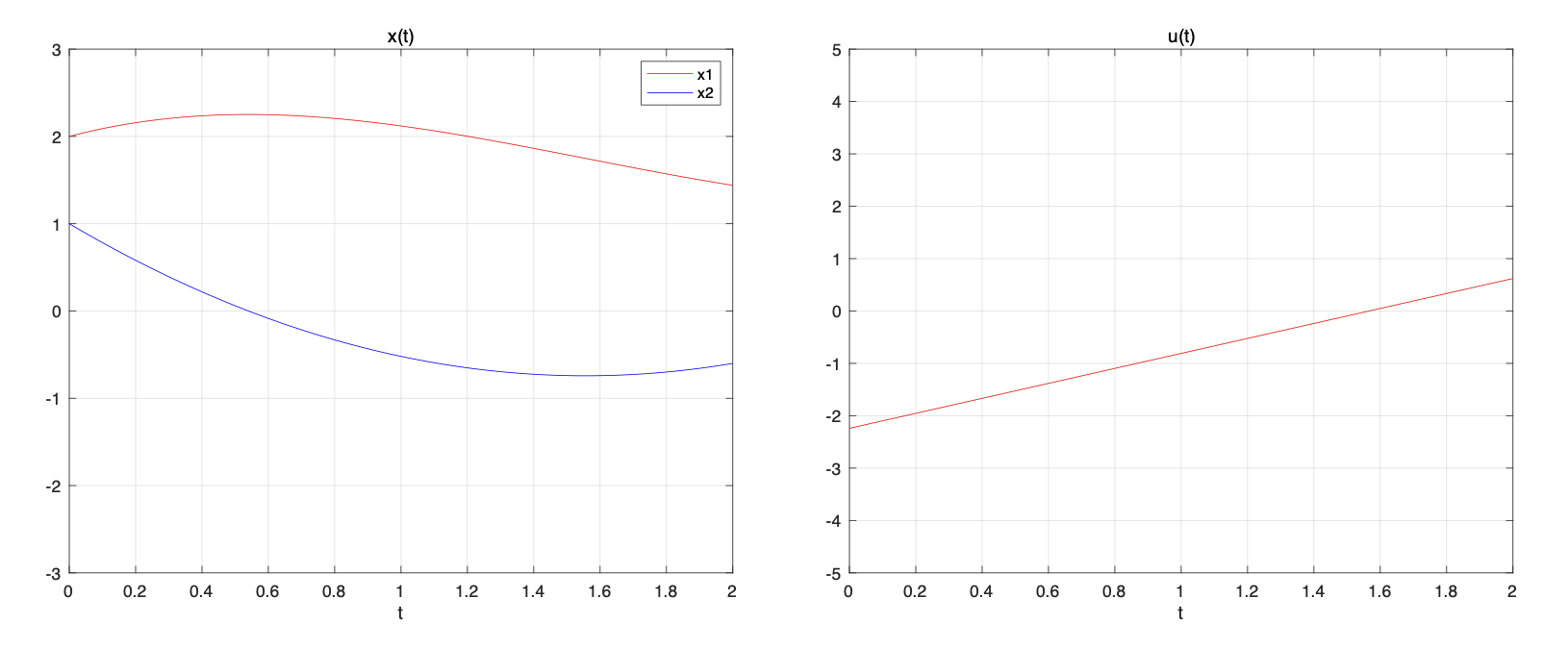
유사 스펙트럴 방법을 적용하기 위하여, 먼저 우선 시간구간 \(t \in [0, 2]\) 를 표준 시간구간인 \(\tau \in [-1, 1]\) 로 변경한다. 시간 변환 관계식은 다음과 같다.
\[ t= \frac{t_f-t_0}{2} \tau + \frac{t_f+t_0}{2} = \tau +1 \]
그러면 시스템 방정식은 다음과 같이 변환된다.
\[ \begin{align} \dot{x}_1 (\tau) &=x_2 (\tau) \\ \\ \dot{x}_2 (\tau) &=u( \tau) \end{align} \]
목적함수는 각각 다음과 같이 변환된다.
\[ \begin{align} J_1 &= \frac{1}{2} \int_{-1}^1 u^2 (\tau) \ d \tau \\ \\ J_2 &= \frac{1}{2} \left(x_1^2 (1)+x_2^2 (1) \right)+ \frac{1}{2} \int_{-1}^1 u^2 (\tau) \ d \tau \end{align} \]
'유도항법제어 > 최적제어' 카테고리의 다른 글
| [PSOC-10] 라다우 유사 스펙트럴 (RPM) 기반 최적제어 (0) | 2023.07.18 |
|---|---|
| [PSOC-9] 로바토 유사 스펙트럴 (LPM) 기반 최적제어 (0) | 2023.07.17 |
| 동역학 문제의 최적제어 문제로의 변환 (0) | 2023.06.04 |
| [Continuous-Time] LQR 예제 : 비례항법유도 법칙 (0) | 2023.04.23 |
| [Continuous-Time] LQR 예제 : 타격각 제어 (0) | 2023.04.22 |




댓글