로바토 유사 스펙트럴 방법(LPM, Lobatto pseudospectral method)에서는 콜로케이션 포인트와 보간점이 동일하다. \(N\) 개의 LGL(Legendre-Gauss-Lobatto) 포인트를 콜로케이션 포인트와 보간점으로 모두 사용한다.

LGL 포인트는 \((N-1)\) 차 르장드르(Legendre) 미분 다항식 \(\dot{P}_{N-1} (\tau)\) 의 해와 \(\tau=-1, \ \tau=1\) 로 구성되어 있다.
로바토 유사 스펙트럴 방법에서는 상태변수 \(\mathbf{x}(\tau)\) 를 \((N-1)\)차 라그랑지 다항식으로 근사화한다.
\[ \mathbf{x}( \tau ) \approx \mathbf{X} (\tau)= \sum_{i=1}^N \mathbf{X}_i L_i (\tau) \tag{1} \]
여기서 \(\mathbf{X}_i= \mathbf{X}(\tau_i ) \in \mathbb{R}^n\) 이고 \(L_i (\tau)\) 는 \((N-1)\) 차 라그랑지 다항식으로 다음과 같다.
\[ L_i (\tau)= \prod_{ \begin{matrix} k=1 \\ k \ne i \end{matrix} }^N \frac{\tau-\tau_k}{\tau_i-\tau_k } \tag{2} \]
\(N\) 개의 LGL 콜로케이션 포인트에서 상태변수 \(\mathbf{x}( \tau)\) 의 근사해는 다음과 같이 운동 미분방정식을 정확히 만족시켜야 한다.
\[ \begin{align} \frac{d \mathbf{x}( \tau)}{d \tau} & = \frac{(t_f-t_0 )}{2} \mathbf{f}(\mathbf{x}(\tau), \mathbf{u}(\tau), \tau, t_0, t_f ) \\ \\ \to \dot{\mathbf{X}}(\tau_j ) &= \sum_{i=1}^N \mathbf{X}_i \dot{L}_i (\tau_j ) \tag{3} \\ \\ & = \frac{(t_f-t_0)}{2} \mathbf{f}( \mathbf{X}_j, \mathbf{U}_j, \tau_j, t_0, t_f ), \ \ \ \ j=1, ..., N \end{align} \]
여기서 \(\mathbf{U}_i \in \mathbb{R}^p\) 이다. \(\dot{L}_i (\tau_j )=D_{ji}\) 로 치환하고 위 식을 행렬식으로 바꾸면 다음과 같다.
\[ \begin{bmatrix} D_{11} & \cdots & D_{1N} \\ \vdots & \ddots & \vdots \\ D_{N1} & \cdots & D_{NN} \end{bmatrix} \begin{bmatrix} \mathbf{X}_1^T \\ \vdots \\ \mathbf{X}_N^T \end{bmatrix} = \frac{(t_f-t_0 )}{2} \begin{bmatrix} \mathbf{f}^T ( \mathbf{X}_1, \mathbf{U}_1, \tau_1, t_0, t_f ) \\ \vdots \\ \mathbf{f}^T (\mathbf{X}_N, \mathbf{U}_N, \tau_N, t_0, t_f) \end{bmatrix} \tag{4} \]
여기서 \([D_{ji} ] \in \mathbb{R}^{N \times N}\) 이다. 목적함수는 다음과 같이 \(N\) 개의 LGL 포인트를 이용한 가우시안 쿼드래처로 근사화 된다.
\[ \begin{align} J & = \phi (\mathbf{x}(-1), \mathbf{x}(1), t_0, t_f )+ \frac{(t_f-t_0 )}{2} \int_{-1}^1 g( \mathbf{x}(\tau), \mathbf{u}( \tau), \tau, t_0, t_f) \ d \tau \\ \\ \to J &= \phi( \mathbf{X}_1, \mathbf{X}_N, t_0, t_f )+ \frac{(t_f-t_0 )}{2} \sum_{j=1}^N w_j \ g( \mathbf{X}_j, \mathbf{U}_j, \tau_j, t_0, t_f ) \tag{5} \end{align} \]
여기서 \(w_j\) 는 LGL 쿼드래처 포인트의 가중치(weighting)다. 경계조건은 다음과 같다.
\[ \begin{align} & \psi( \mathbf{x}(-1), \mathbf{x}(1), t_0, t_f )=0 \\ \\ \to \ & \psi (\mathbf{X}_1, \mathbf{X}_N, t_0, t_f )=0 \tag{6} \end{align} \]
경로제약 조건은 \(N\) 개의 LGL 포인트에서 다음 식을 만족해야 한다.
\[ \begin{align} & \frac{(t_f-t_0 )}{2} \mathbf{C}( \mathbf{x} (\tau), \mathbf{u}(\tau), \tau, t_0, t_f ) \le 0 \\ \\ \to \ & \frac{(t_f-t_0)}{2} \mathbf{C}( \mathbf{X}_j, \mathbf{U}_j, \tau_j, t_0, t_f ) \le 0 , \ \ \ j=1, ..., N \tag{7} \end{align} \]
로바토 유사 스펙트럴에서 유도된 비선형 프로그래밍 문제(NLP)는 식 (4), (6), (7) 의 대수적 제약 조건에 따라 식 (5)의 목적함수를 최소화하는 것이다. 이 때 최적화 대상 변수는 다음과 같다.
\[ (\mathbf{X}_1, \ \mathbf{X}_2, \ ... , \ \mathbf{X}_N ), \ ( \mathbf{U}_1, \ \mathbf{U}_2, \ ... , \ \mathbf{U}_N ), \ t_0, \ t_f \tag{8} \]
여기서 \(t_0, \ t_f\) 는 최적제어 문제에 따라서 변수가 될 수도 아닐 수도 있다.
콜로케이션 포인트에서 제어입력 값 \(\mathbf{U}_i\) 를 계산한 후 다음과 같이 \((N-1)\) 차 라그랑지 보간법을 이용하여 제어입력의 시간 함수를 구할 수 있다.
\[ \mathbf{u}(\tau) \approx \mathbf{U}(\tau)= \sum_{i=1}^N \mathbf{U}_i L_i (\tau) \tag{9} \]
이제 앞선 포스팅(https://pasus.tistory.com/281)에 있는 최적제어 예제 (a)를 LPM을 이용하여 풀어보자. 최적제어 문제를 정적 파라미터 최적화 문제로 변환되는 과정을 자세히 살펴보기 위해서 콜로케이션 포인트의 숫자를 작게 잡도록 한다. 여기서는 4개의 LGL 콜로케이션 포인트를 사용한다. LGL 콜로케이션 포인트와 보간점은 다음과 같다.
N = 4; % number of collocation points
points = GaussPoints(N,'LGL'); % LGL collocation points (N)
col_point = points'
int_point = col_point; % interpolating points N
col_point =
-1.0000 -0.4472 0.4472 1.0000
식 (1)에 의하면 상태변수는 보간점을 이용하여 다음과 같이 이산화된다.
\[ \begin{align} & x_1 (\tau) \approx X_1 (\tau)= \sum_{i=1}^4 X_{i1} L_i (\tau) \\ \\ & x_2 (\tau) \approx X_2 (\tau)= \sum_{i=1}^4 X_{i2} L_i (\tau) \end{align} \]
3차 라그랑지 다항식은 다음과 같다.
\[ L_i (\tau)= \prod_{ \begin{matrix} k=1 \\ k \ne i \end{matrix} }^4 \frac{\tau-\tau_k}{\tau_i-\tau_k } \]
콜로케이션 포인트에서 미분방정식을 만족해야 하므로 식 (3)에 의하면 다음 식을 유도할 수 있다.
\[ \begin{align} & \dot{x}_1 (\tau)=x_2 (\tau) \\ \\ & \dot{x}_2(\tau)=u(\tau) \\ \\ \to \ & \dot{X}_1 (\tau_j )= \sum_{i=1}^4 X_{i1} \dot{L}_i (\tau_j )=X_{j2} \\ \\ & \dot{X}_2 (\tau_j )= \sum_{i=1}^4 X_{i2} \dot{L}_i (\tau_j ) =U_j, \ \ \ \ \ j=1, ..., 4 \end{align} \]
식 (4)에 의하면 위 식의 행렬 형식은 다음과 같다.
\[ \begin{bmatrix} D_{11} & D_{12} & D_{13} & D_{14} \\ D_{21} & D_{12} & D_{23} & D_{24} \\ D_{31} & D_{32} & D_{33} & D_{34} \\ D_{41} & D_{42} & D_{43} & D_{44} \end{bmatrix} \begin{bmatrix} X_{11} & X_{12} \\ X_{21} & X_{22} \\ X_{31} & X_{32} \\ X_{41} & X_{42} \end{bmatrix} = \begin{bmatrix} X_{12} & U_1 \\ X_{22} & U_2 \\ X_{32} & U_3 \\ X_{42} & U_4 \end{bmatrix} \]
Dji = LagrangePolyDerivative(col_point,int_point) % Differentiation matrix
Dji =
-3.0000 4.0451 -1.5451 0.5000
-0.8090 -0.0000 1.1180 -0.3090
0.3090 -1.1180 -0.0000 0.8090
-0.5000 1.5451 -4.0451 3.0000
목적함수는 콜로케이션 포인트를 이용한 가우시안 쿼드래처로 근사화 시킨다.
\[ \begin{align} & J_1= \frac{1}{2} \int_{-1}^1 u^2 (\tau) \ d \tau \\ \\ \to \ & J_1= \frac{1}{2} \sum_{j=1}^4 w_j U_j^2 \end{align} \]
gweights = GaussianQuadrature(N,'LGL') % LGL quadrature weights
gweights =
0.1667 0.8333 0.8333 0.1667
초기조건과 최종조건은 다음과 같다.
\[ \begin{align} & x_1 (-1)=2, \ x_2 (-1)=1, \ x_1 (1)=0, \ x_2 (1)=0 \\ \\ \to \ & X_{11}=2, \ X_{12}=1, \ X_{41}=0,\ X_{42}=0 \end{align} \]
위 식을 종합하면 다음과 같은 정적 파라미터 최적화 문제를 구성할 수 있다.
\[ \begin{align} & \min J_1 = \frac{1}{2} \sum_{j=1}^4 w_j U_j^2 \\ \\ & \mbox{subject to }: \\ \\ & \ \ \ \ \ \begin{bmatrix} D_{11} & D_{12} & D_{13} & D_{14} \\ D_{21} & D_{12} & D_{23} & D_{24} \\ D_{31} & D_{32} & D_{33} & D_{34} \\ D_{41} & D_{42} & D_{43} & D_{44} \end{bmatrix} \begin{bmatrix} X_{11} & X_{12} \\ X_{21} & X_{22} \\ X_{31} & X_{32} \\ X_{41} & X_{42} \end{bmatrix} = \begin{bmatrix} X_{12} & U_1 \\ X_{22} & U_2 \\ X_{32} & U_3 \\ X_{42} & U_4 \end{bmatrix} \\ \\ & \ \ \ \ \ X_{11}=2, \ X_{12}=1, \ X_{41}=0,\ X_{42}=0 \end{align} \]
매트랩의 비선형 최적화 문제 솔버인 fmincon 함수를 이용하여 위 문제를 풀면 다음과 같다.
\[ \begin{align} & \begin{bmatrix} X_{11} & X_{12} \\ X_{21} & X_{22} \\ X_{31} & X_{32} \\ X_{41} & X_{42} \end{bmatrix} = \begin{bmatrix} 2 & 1 \\ 1.718 & -1.416 \\ 0.17 & -1.024 \\ 0 & 0 \end{bmatrix} \\ \\ & \begin{bmatrix} U_1 \\ U_2 \\ U_3 \\ U_4 \end{bmatrix} = \begin{bmatrix} -5 \\ -2.5125 \\ 1.5125 \\ 4 \end{bmatrix} \end{align} \]
아래 그림은 라그랑지 보간 다항식을 이용하여 상태변수와 제어입력의 반응을 그린 것이다. 해석적으로 구한 상태변수와 제어입력의 반응과 일치함을 알 수 있다.
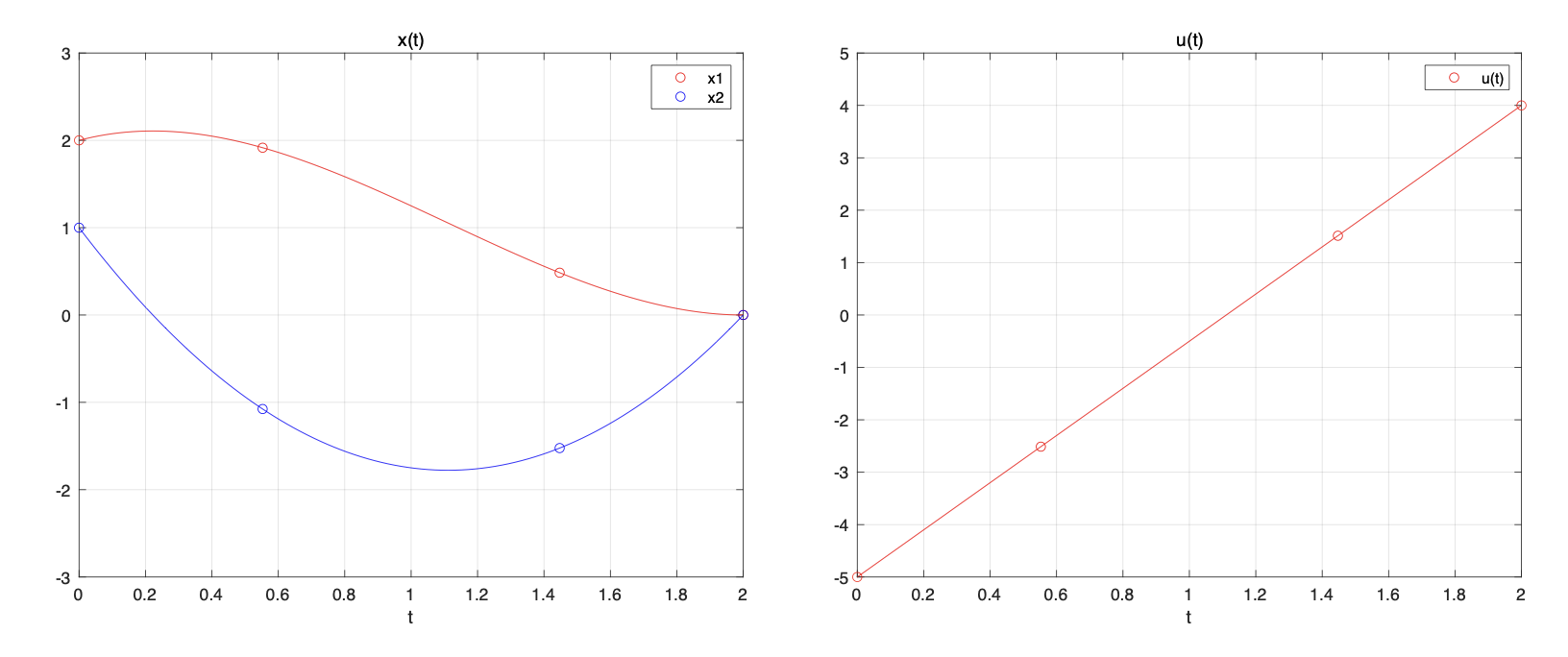
다음으로 같은 포스팅(https://pasus.tistory.com/281)에 있는 최적제어 예제 (b)를 LPM을 이용하여 풀어보자.
예제 (a)와 똑같은 LGL 콜로케이션 포인트와 보간점을 사용한다. 예제 (a)와의 차이점은 목적함수와 경계조건에 있다. 목적함수는 다음과 같다.
\[ \begin{align} & J_2= \frac{1}{2} ( x_1^2 (1)+x_2^2 (1))+ \frac{1}{2} \int_{-1}^1 u^2 (\tau) \ d \tau \\ \\ \to \ & J_2= \frac{1}{2} (X_{41}^2+X_{42}^2 )+ \frac{1}{2} \sum_{j=1}^4 w_j U_j^2 \end{align} \]
초기조건은 다음과 같다.
\[ \begin{align} & x_1 (-1)=2, \ \ x_2 (-1)=1 \\ \\ \to \ & X_{11}=2, \ \ X_{12}=1 \end{align} \]
정리하면 다음과 같은 정적 파라미터 최적화 문제로 변환시킬 수 있다.
\[ \begin{align} & \min J_2= \frac{1}{2} (X_{41}^2+X_{42}^2 )+ \frac{1}{2} \sum_{j=1}^4 w_j U_j^2 \\ \\ & \mbox{subject to }: \\ \\ & \ \ \ \ \ \begin{bmatrix} D_{11} & D_{12} & D_{13} & D_{14} \\ D_{21} & D_{12} & D_{23} & D_{24} \\ D_{31} & D_{32} & D_{33} & D_{34} \\ D_{41} & D_{42} & D_{43} & D_{44} \end{bmatrix} \begin{bmatrix} X_{11} & X_{12} \\ X_{21} & X_{22} \\ X_{31} & X_{32} \\ X_{41} & X_{42} \end{bmatrix} = \begin{bmatrix} X_{12} & U_1 \\ X_{22} & U_2 \\ X_{32} & U_3 \\ X_{42} & U_4 \end{bmatrix} \\ \\ & \ \ \ \ \ X_{11}=2, \ X_{12}=1 \end{align} \]
매트랩의 비선형 최적화 문제 솔버인 fmincon 함수를 이용하여 위 문제를 풀면 다음과 같다.
\[ \begin{align} & \begin{bmatrix} X_{11} & X_{12} \\ X_{21} & X_{22} \\ X_{31} & X_{32} \\ X_{41} & X_{42} \end{bmatrix} = \begin{bmatrix} 2 & 1 \\ 2.2511 & -0.0189 \\ 1.8251 & -0.7430 \\ 1.4286 & -0.6190 \end{bmatrix} \\ \\ & \begin{bmatrix} U_1 \\ U_2 \\ U_3 \\ U_4 \end{bmatrix} = \begin{bmatrix} -2.2381 \\ -1.4484 \\ -0.1706 \\ 0.6190 \end{bmatrix} \end{align} \]
아래 그림은 라그랑지 보간 다항식을 이용하여 상태변수와 제어입력의 반응을 그린 것이다. 해석적으로 구한 상태변수와 제어입력의 반응과 일치함을 알 수 있다.

'유도항법제어 > 최적제어' 카테고리의 다른 글
| [PSOC-11] 가우스 유사 스펙트럴 (GPM) 기반 최적제어 (0) | 2023.07.20 |
|---|---|
| [PSOC-10] 라다우 유사 스펙트럴 (RPM) 기반 최적제어 (0) | 2023.07.18 |
| [PSOC-8] 유사 스펙트럴 기반 최적제어 문제 (0) | 2023.07.17 |
| 동역학 문제의 최적제어 문제로의 변환 (0) | 2023.06.04 |
| [Continuous-Time] LQR 예제 : 비례항법유도 법칙 (0) | 2023.04.23 |




댓글