[Continuous-Time] LQR 예제 : 비례항법유도 법칙

이전 포스트(https://pasus.tistory.com/259)와 동일한 문제를 풀어본다. 다만 최종시간에서 $y(t_f)$ 는 주어지지만 $\theta (t_f)$ 에 관한 제약조건은 없는 경우이다.

 

 

편의상 비행체의 선형화된 운동 방정식을 다시 쓴다.

 

$$\begin{array}{r}\text{(1)}& & \dot{x}\approx V\\ & \dot{y}\approx V\theta \\ \\ & \dot{\theta }=\frac{a}{V}\end{array}$$

 

여기서 $a$ 는 비행체의 가속도로서 제어변수, $\theta$ 는 x-축과 비행체의 속도벡터 사이의 비행 방향각으로서 매우 작다고 가정한 것이다. 비용함수와 제약조건은 다음과 같다.

 

$$\begin{array}{r}\text{(2)}& & J=\frac{1}{2}{\int }_0^{t_f}{a}^2(t)dt\\ & y(0)=0,\theta (0)={\theta }_0,y(t_f)=y_f\end{array}$$

 

제어 목적은 출발지에서 출발하여 비행 시간 $t_f$ 가 경과한 후 목적지에 최소의 에너지를 사용하여 비행체를 목적지 $(x_f,y_f)$에 도착시키는 것이다. 그림에 비행체와 목적지, 출발지 간의 기하학적인 관계가 나와 있다.

 

 

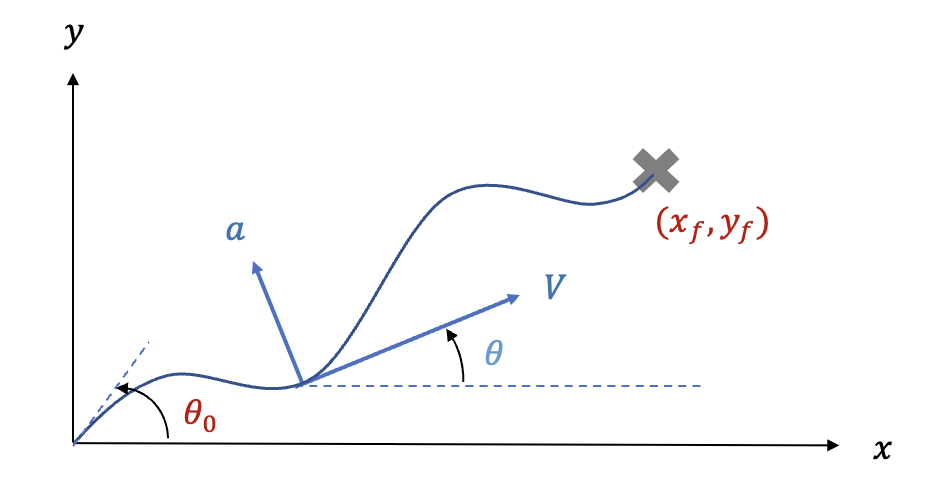
이 문제는 최종상태가 설정된 LQR 문제 (https://pasus.tistory.com/257)의 해를 이용하여 풀 수 있다. 우선 시스템 운동 방정식 (1)을 LQR 문제에 맞게 상태변수 방정식으로 바꾼다.

 

$$\begin{array}{}\text{(3)}& \dot{\mathbf{x}}=A\mathbf{x}+B\mathbf{u}\end{array}$$

여기서

$$\begin{array}{rl}& A=\left[\begin{array}{cc}0& V\\ 0& 0\end{array}\right],B=\left[\begin{array}{c}0\\ 1/V\end{array}\right],\mathbf{u}=a\\ \\ & \mathbf{x}(t)=\left[\begin{array}{c}y\\ \theta \end{array}\right],\mathbf{x}(0)=\left[\begin{array}{c}0\\ {\theta }_0\end{array}\right]\end{array}$$

 

이다. 최종 상태변수의 제약조건은 다음과 같다.

 

$$\begin{array}{r}\text{(4)}& & C\mathbf{x}(t_f)={\mathbf{r}}_f=y_f\\ & C=\left[\begin{array}{cc}1& 0\end{array}\right]\end{array}$$

 

그러면 시스템 모델과 제약조건이 식 (3)과 (4)로 주어지고 비용함수가 식 (2)로 주어졌을 때 최적제어는 다음과 같이 계산할 수 있다.

 

$$\begin{array}{}\text{(5)}& \mathbf{u}(t)=-B^{T}S(t)\mathbf{x}(t)-B^T\mathbf{V}(t)P^{-1}(t)({\mathbf{r}}_f-{\mathbf{V}}^T(t)\mathbf{x}(t))\end{array}$$

여기서

$$\begin{array}{r}\text{(6)}& S(t)& =0\\ \text{(7)}& -\dot{\mathbf{V}}(t)& =A^T\mathbf{V},t\le t_f,\mathbf{V}(t_f)=C^T\\ \text{(8)}& \dot{P}(t)& ={\mathbf{V}}^{T}B{B}^T\mathbf{V},t\le t_f,P(t_f)=0\end{array}$$

 

이다. 이제 식 (5)를 구성하는 행렬을 차례로 계산해 보자. 먼저 식 (7)을 계산한다.

 

$$\begin{array}{}\text{(9)}& -\left[\begin{array}{c}{\dot{v}}_1\\ {\dot{v}}_2\end{array}\right]=\left[\begin{array}{cc}0& 0\\ V& 0\end{array}\right]\left[\begin{array}{c}{v}_1\\ v_2\end{array}\right],\left[\begin{array}{c}{v}_1(t_f)\\ v_2(t_f)\end{array}\right]=\left[\begin{array}{c}1\\ 0\end{array}\right]\end{array}$$

 

여기서 $\mathbf{V}=[v_1{v}_2{]}^T$ 이다. 위 식을 전개하면 다음과 같다.

 

$$\begin{array}{r}\text{(10)}& & {\dot{v}}_1=0,v_1(t_f)=1\\ & {\dot{v}}_2=-v_{1}V,v_2(t_f)=0\end{array}$$

위 식을 풀면,

$$\begin{array}{r}\text{(11)}& & v_1(t)=1\\ & v_2(t)=V(t_f-t)\end{array}$$

 

이 된다. 다음으로 식 (8)을 계산한다.

 

$$\begin{array}{r}\text{(12)}& \dot{P}& =[v_1{v}_2]\left[\begin{array}{cc}0& 0\\ 0& 1/V^2\end{array}\right]\left[\begin{array}{c}{v}_1\\ v_2\end{array}\right]\\ & =\frac{v_2^2}{V^2}=(t_f-t{)}^2,P(t_f)=0\end{array}$$

위 식을 풀면,

$$\begin{array}{}\text{(13)}& P(t)=-\frac{(t_f-t{)}^3}{3}\end{array}$$

 

이 된다. 식 (11)과 (13)을 식 (5)에 대입하면 최적제어는 다음과 같다.

 

$$\begin{array}{r}\text{(14)}& a(t)& =[01/V]\left[\begin{array}{c}1\\ V{t}_{go}\end{array}\right]\frac{3}{t_{go}^3}(y_f-(y+V{t}_{go}\theta ))\\ & =\frac{3}{t_{go}^2}(y_f-y)-\frac{3V}{t_{go}}\theta \end{array}$$

여기서 $t_{go}=t_f-t$ 로서 잔여비행시간(time-to-go)이다.

 

 

식 (14)는 미사일의 유도법칙으로 사용될 수 있다. 미사일 유도법칙에서 사용되는 변수로 식 (14)를 변형하여 보자.

 

 

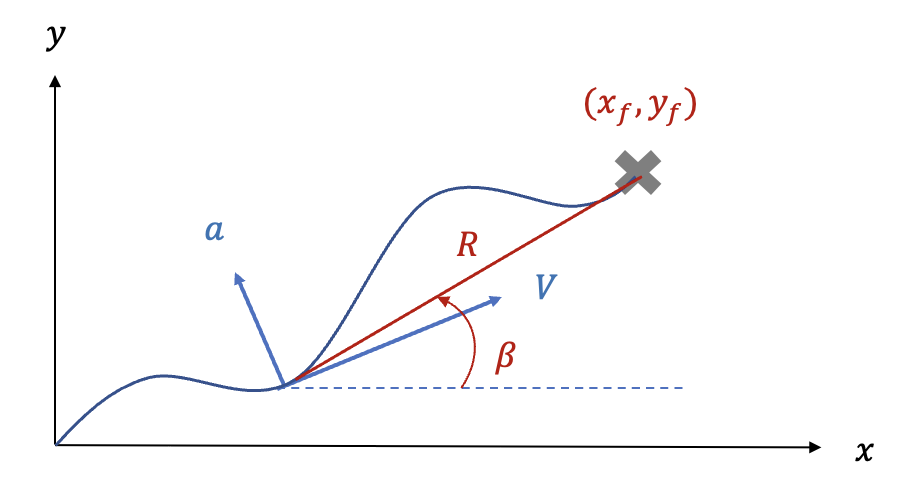
위 그림에서 $\beta$ 는 시선각(line-of-sight angle)이다. 시선각은 다음과 같이 계산할 수 있다.

 

$$\begin{array}{}\text{(15)}& \beta (t)={\sin }^{-1}\frac{(y_f-y)}{R}\approx \frac{(y_f-y)}{R}\approx \frac{(y_f-y)}{V{t}_{go}}\end{array}$$

여기서 $R$ 은 표적까지의 거리로서 $V{t}_{go}$ 로 근사할 수 있다. 식 (15)를 식 (14)에 대입하면 최적제어는 다음과 같이 된다.

 

$$\begin{array}{}\text{(16)}& a(t)=\frac{3V}{t_{go}}\beta -\frac{3V}{t_{go}}\theta \end{array}$$

식 (15)의 시선각을 미분하면 다음과 같이 된다.

 

$$\begin{array}{}\text{(17)}& \dot{\beta }(t)=\frac{-\dot{y}V{t}_{go}+V(y_f-y)}{V^2{t}_{go}^2}=-\frac{\dot{y}}{V{t}_{go}}+\frac{\beta }{t_{go}}\end{array}$$

위 식에 식 (1)을 대입하면,

 

$$\begin{array}{}\text{(18)}& \dot{\beta }(t)\approx -\frac{V\theta }{V{t}_{go}}+\frac{\beta }{t_{go}}=\frac{1}{t_{go}}(\beta -\theta )\end{array}$$

이 되므로 시선각을 시선각의 변화율과 비행 방향각의 함수로 표현할 수 있다.

 

$$\begin{array}{}\text{(19)}& \beta (t)=\theta (t)+t_{go}\dot{\beta }(t)\end{array}$$

 

식 (19)를 식 (16)에 대입하면 최종적으로 최적제어 또는 미사일의 유도법칙은 다음과 같이 된다.

 

$$\begin{array}{r}\text{(20)}& a(t)& =\frac{3V}{t_{go}}(\theta +t_{go}\dot{\beta }(t))-\frac{3V}{t_{go}}\theta \\ & =3V\dot{\beta }(t)\end{array}$$

식 (20)에 의하면 미사일의 최적 유도법칙은 항법상수가 $3$ 인 비례항법유도(PNG)법칙임을 알 수 있다.