LTI 시스템의 임펄스 반응 \( h[n] \)과 입력 신호 \( x[n] \)의 컨볼루션(convolution)은 다음 식으로 정의한다.
\[ y[n] = \sum_{k=-\infty}^{\infty} x[k] h[n-k] \]
한편, LSI 시스템의 임펄스 반응 \( h[m,n] \)과 입력 신호 \( x[m,n] \)의 2D 컨볼루션은 다음 식으로 정의한다.
\[ y[m,n] = \sum_{k=-\infty}^{\infty} \sum_{l=-\infty}^{\infty} x[k,l] h[m-k, n-l] \]
컨볼루션은 앞에서 설명했듯이 LTI 또는 LSI 시스템에 입력신호가 가해졌을 때 출력신호를 계산하는 식이며, 컨볼루션은 ‘뒤집기와 이동’ 방법을 사용하여 계산할 수 있다.
상관도(correlation)의 공식은 컨볼루션과 유사하다. 동일한 신호 \( x[n] \)의 자기 상관도(auto-correlation)는 다음과 같이 정의한다.
\[ R_{xx}[n] = \sum_{k=-\infty}^{\infty} x[k] x[n+k] \]
서로 다른 두 신호 \( h[n] \)과 \( x[n] \)의 상호 상관도(cross-correlation)는 다음과 같이 정의한다.
\[ R_{xh}[n] = \sum_{k=-\infty}^{\infty} x[k] h[n+k] \]
2D 신호인 \( x[m,n] \)과 \( h[m,n] \)의 경우 자기 상관도와 상호 상관도는 각각 다음과 같이 정의한다.
\[ \begin{align} R_{xx}[m,n] &= \sum_{k=-\infty}^{\infty} \sum_{l=-\infty}^{\infty} x[k,l] x[m+k, n+l] \\ \\ R_{xh}[m,n] &= \sum_{k=-\infty}^{\infty} \sum_{l=-\infty}^{\infty} x[k,l] h[m+k, n+l] \end{align} \]
공식으로 볼 때 컨볼루션과 상관도의 차이점은 컨볼루션의 \( – \)(마이너스) 자리에 상관도의 경우 \( + \)(플러스)가 있는 것뿐이다. 따라서 상관도를 계산할 때는 컨볼루션에서 하던 ‘뒤집기’가 제외되고 ‘이동’ 방법만 사용된다.
다음 그림은 2D 컨볼루션과 상관도의 계산상 차이점을 보여준다. 컨볼루션의 경우 신호의 ‘이동’ 전에 ‘뒤집기’를 먼저해야 한다.

그리고 ‘이동’하면서 계산한다.

반면에 상관도는 신호의 ‘뒤집기’ 없이 ‘이동’만으로 계산한다.

상관도(correlation)는 두 신호의 유사성을 측정하는데 사용된다. 두 신호가 일치할 때 상관도 값이 최대가 되며 유사성이 떨어질수록 그 값이 작아진다.
예를 들면, GPS 수신기에서는 수신된 신호가 어느 GPS위성에서 송신된 신호인지 결정하고, 그 신호가 위성에서부터 수신기까지 도달하는데 걸리는 전송 시간을 계산하는 데 사용된다.
아래 그림은 GPS에서 생성한 PRN3 신호, 위성에서 수신하여 전송 시간인 700 chip 만큼 지연(delay)된 PRN3 신호와, 두 신호 사이의 자기 상관도를 보여준다. 정확히 700 chip에서 상관도가 제일 큰 값을 가지며 그 외에서는 상관도 값이 거의 0을 유지하는 것을 볼 수 있다.
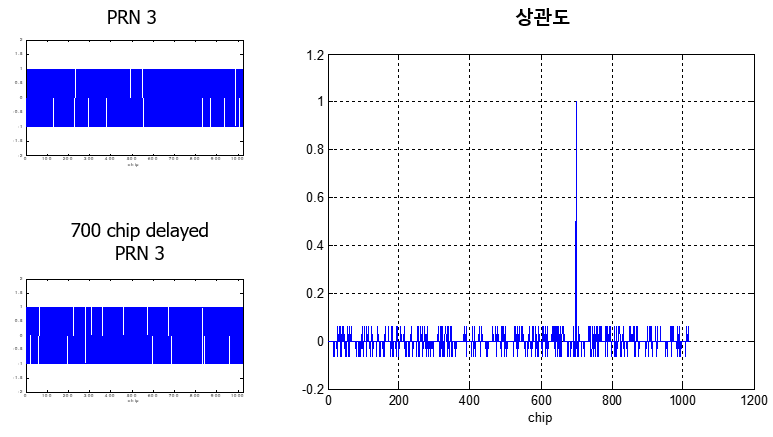
참고로 여기서 chip 이란 C/A(coarse/acquisition)코드의 구성 요소인 0과 1을 의미하며 C/A코드는 총 1023개의 칩으로 구성되었으며 1 chip을 거리로 환산하면 300 m이다. 각 GPS 위성에는 고유한 PRN(Pseudo Random Noise) 번호가 부여되어 있다. GPS의 C/A코드는 서로 다른 위성 간의 신호를 구별하기 위해서 상호 상관도가 거의 0이 되도록 설계되어 있다.
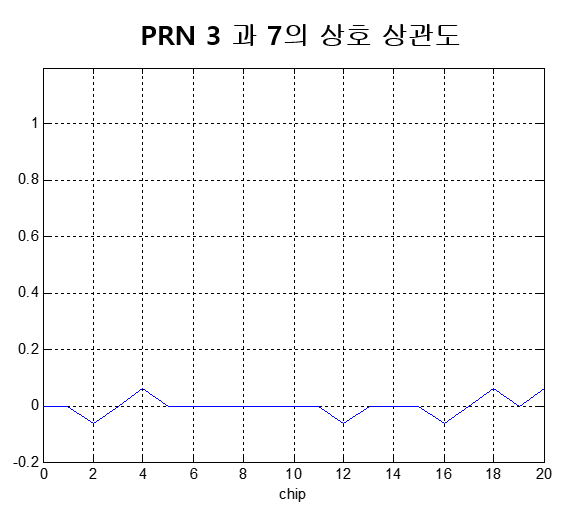
다음 그림은 PRN3의 자기 상관도와 PRN3와 PRN7 신호의 상호 상관도를 그린 것이다. 모든 구간에서 값이 거의 0인 것을 알 수 있다.
2D 이미지 신호의 경우에는 어떤 이미지에서 특정 이미지 부분이 속해 있는 지와 속해 있다면 위치가 어디인지 알고 싶을 때, 상관도를 이용할 수 있다.
예를 들어서 다음과 같이 레이싱카 이미지에서

이미지의 왼쪽을 보면 다음과 같이 ‘SPORT SHOES’라는 광고판을 볼 수 있다. 이 부분을 잘라서 별도의 작은 이미지로 만들고,

원래의 레이싱카 이미지와 광고판의 이미지의 상호 상관도를 계산하면 다음과 같이 최고 상관값을 갖는 위치를 계산해 낼 수 있다.

그 부분을 원래 이미지에 빨강색 박스로 표시해 보면, 상호 상관도가 레이싱카 이미지에서 ‘SPORT SHOES’라는 광고판의 위치를 정확히 판별할 수 있음을 알 수 있다.

결론적으로 말하면 컨볼루션과 상관도는 수식이 매우 유사하지만, 컨볼루션은 LTI 또는 LSI 시스템의 입출력 관계를 나타내고 상관도는 두 신호의 유사성을 측정하는 것으로서, 서로 다른 개념이다.
'AI 딥러닝 > DLA' 카테고리의 다른 글
| [U-Net] 망막 혈관 세그멘테이션 (Retinal Vessel Segmentation) (0) | 2022.05.11 |
|---|---|
| [U-Net] U-Net 구조 (0) | 2022.05.11 |
| [CNN] 이미지 필터 설계해 보기 (0) | 2020.07.29 |
| [CNN] 2D 컨볼루션 계산하기 (0) | 2020.07.29 |
| [CNN] 2D 컨볼루션 (0) | 2020.07.28 |




댓글