앞서 살펴본 바와 같이(https://pasus.tistory.com/263) VAE의 손실함수는 복원손실 항과 정규화 손실 항으로 구성된다.
식 (1)의 VAE 손실함수에서 첫번째 항인 복원손실은 복원(reconstruction)된 데이터가 원본 데이터와 얼마나 유사한지를 나타내는 오차다. 원본 데이터의 확률분포에 따라서 원본 데이터와 복원된 데이터 간의 교차 엔트로피나 L2 놈(norm)을 사용하여 복원손실을 계산할 수 있다.
두번째 항인 정규화(regularization) 손실은 고차원 입력 데이터를 저차원 잠재변수 공간(latent space)으로 인코딩할 때 잠재변수의 확률분포가 사전에(prior) 규정한 확률분포 \(p(\mathbf{z})\) 와 얼마나 유사한지를 계산하는 KL발산(Kullback-Leibler divergence) 항이다.
\[ \mathcal{L}( \phi, \theta)= - \mathbb{E}_q [ \log p_\theta (\mathbf{x} \vert \mathbf{z} ) ]+ \mathbb{KL}( q_\phi (\mathbf{z} \vert \mathbf{x}) \Vert p(\mathbf{z})) \tag{1} \]
AE(오토인코더)는 복원손실만 최소화하지만 VAE는 KL발산 항도 함께 최소화하여 잠재변수의 공간에도 제약을 가한다. 즉 KL발산 항은 잠재공간의 구조에 제약을 가하는 정규화(regularization) 기능을 갖는다.

잠재변수의 확률분포를 정규 가우시안 분포 \(p(\mathbf{z})=\mathcal{N}(0, I)\) 로 규정한다면 인코딩된 데이터가 잠재공간의 중심 주위에 균등하게 분포하도록 강제한다. 공분산이 대각행렬인 가우시안 분포의 경우 랜덤벡터의 구성 요소는 서로 확률적으로 독립(independence)이므로, 잠재변수의 확률분포를 정규 가우시안 분포로 규정하면 잠재벡터의 구성 요소는 서로 독립이 된다. 즉 잠재변수 간에 서로 상관관계가 없어진다.
AE(오토인코더)는 기존의 선형 차원축소(dimension reduction) 방법인 POD(Proper Orthogonal Decomposition)를 비선형 방법으로 일반화시킨 것으로 해석되며 최근 수많은 연구에서 고도의 비선형 문제에 대한 차원축소 모델을 구축하는데 사용되고 있다. 하지만 POD가 직교 기반의 선형공간에서 잠재변수 간의 독립성을 보장하는 것과는 달리 AE의 경우에는 복원손실을 최소화하는 것에만 목표를 두고 잠재공간의 구조를 고려하지 않기 때문에 잠재변수 간의 독립성을 보장할 수 없다.
서로 독립인 또는 상관관계가 없는 잠재변수가 이상적인 이유는 각 잠재변수가 가지고 있는 물리적 의미나 데이터의 특성을 해석하기가 용이하기 때문이다.
이런 관점에서 볼 때 VAE는 KL발산 항을 통하여 차원축소 방법으로서의 AE의 단점을 개선한 것으로 해석할 수 있다. 구글 딥마인드에서 발표한 논문 '\(\beta-\)VAE: Learning Basic Visual Concepts with a Constrained Variational Framework'에서는 이를 보다 일반화하여 다음과 같이 손실함수에 가중치 \(\beta\) 를 도입하여 정규화 항의 영향을 조절할 것을 제안했다.
\[ \mathcal{L}( \phi, \theta)= - \mathbb{E}_q [ \log p_\theta (\mathbf{x} \vert \mathbf{z} ) ]+ \beta \ \mathbb{KL}( q_\phi (\mathbf{z} \vert \mathbf{x}) \Vert p(\mathbf{z})) \tag{2} \]
식 (2)는 VAE의 변형 알고리즘인 \(\beta-\)VAE의 손실함수이다. 가중치 \(\beta\) 가 작은 값을 가지면 \(\beta-\)VAE는 잠재공간을 구조화 하는 대신에 데이터의 복원 품질을 더 향샹시키는데 신경 쓸 것이고, \(\beta\) 가 큰 값을 가지면 잠재공간을 정규화하고 잠재변수 간의 독립성 수준을 개선시키는 데 더 노력할 것이다. 따라서 복원 품질과 잠재변수의 독립성 간에 적절한 조정이 필요하다. \(\beta=1\) 이면 표준 VAE와 동일하다.
관련 논문에 의하면 가중치 \(\beta\) 가 적절히 조정되지 않으면 overpruning 또는 variable-collapse 또는 sparsity 현상이 발생하는 것으로 보고 되었다. 이 현상을 전략적으로 이용하는 방법도 있는데 이에 대해서는 추후 논의하기로 한다.
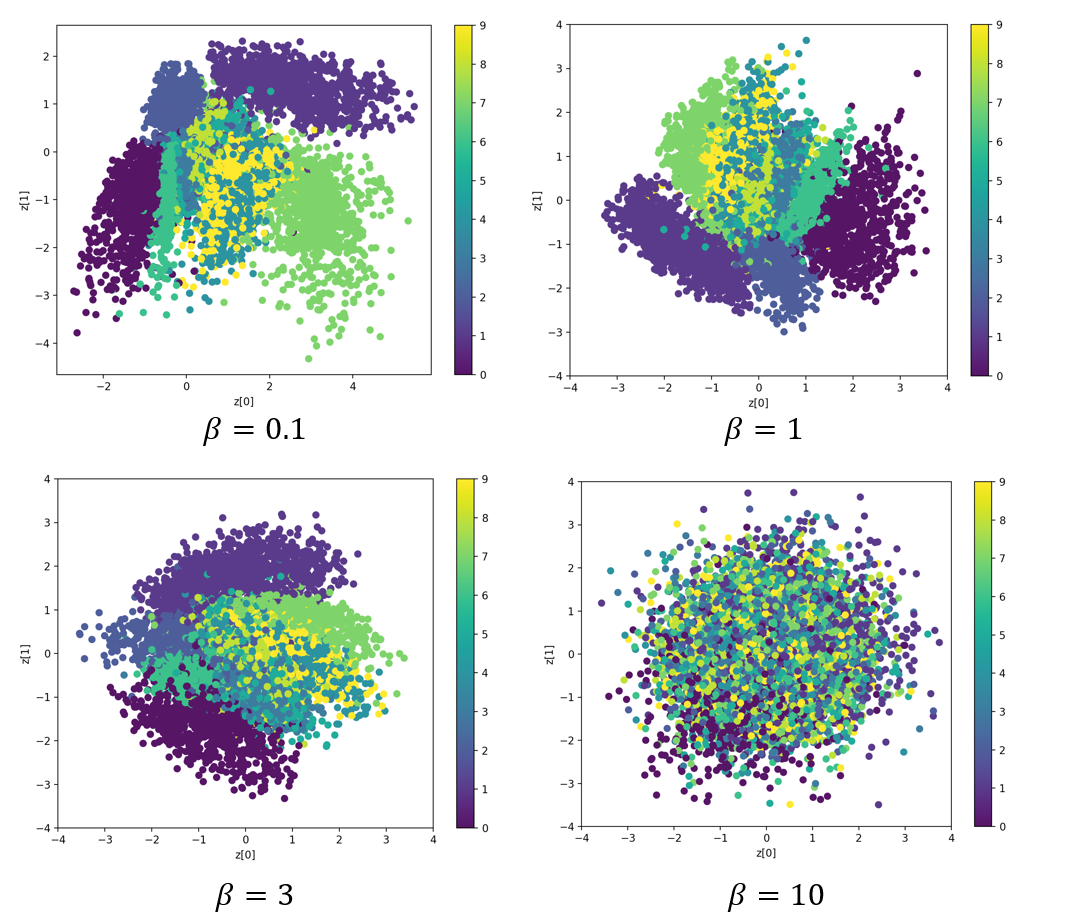
다음은 MNIST 데이터셋을 이용한 \(\beta-\)VAE 실행 결과이다. 먼저 2차원 잠재공간에서의 인코딩된 데이터 분포이다. \(\beta\) 가 작을 때는 데이터가 라벨에 따라서 확연히 구분되는 영역을 차지하고 있지만 \(\beta\) 가 클수록 잠재공간의 중심 주위에 가우시안 분포를 형성하는 것을 알 수 있다.
다음은 복원 성능을 본 것이다. \(\beta\) 가 클수록 복원 품질이 악화되는 것을 알 수 있다.

다음은 잠재공간의 일정 영역을 스캔한 결과다.

\(\beta=0.1\) 일 때와 \(\beta=3\) 을 비교했는데 육안으로는 2차원 잠재공간의 두 축의 상관관계가 확연히 드러나지는 않으나, \(\beta=3\) 의 경우에 \(z_1\) 축으로는 글자의 기울기 정도, 경우에 \(z_2\) 축으로는 글자의 모양의 변화가 관찰된다.
다음은 Tensorflow 2로 작성한 \(\beta-\)VAE 코드다.
vae_model.py
# beta-VAE model for MNIST
# coded by st.watermelon
import tensorflow as tf
from tensorflow.keras.layers import Conv2D, Dense, Conv2DTranspose, Reshape
from tensorflow.keras.models import Model
""" beta-VAE encoder """
class Encoder(Model):
def __init__(self, latent_dim):
super(Encoder, self).__init__()
self.h1 = Conv2D(32, 3, strides=2, padding='same', activation='relu')
self.h2 = Conv2D(64, 3, strides=2, padding='same', activation='relu')
self.h3 = Dense(16, activation='relu')
self.flatten = tf.keras.layers.Flatten()
self.mu = Dense(latent_dim)
self.log_var = Dense(latent_dim)
def call(self, x):
x = self.h1(x) # input size (28,28,1)
x = self.h2(x) # (7,7,64)
x = self.flatten(x) # (latent_dim*7*7*64)
x = self.h3(x)
mu = self.mu(x)
log_var = self.log_var(x)
return mu, log_var
""" decoder """
class Decoder(Model):
def __init__(self):
super(Decoder, self).__init__()
self.fc = Dense(7*7*64, activation='relu')
self.reshape = Reshape((7, 7, 64))
self.h1 = Conv2DTranspose(64, 3, strides=2, padding='same', activation='relu')
self.h2 = Conv2DTranspose(32, 3, strides=2, padding='same', activation='relu')
self.output_layer = Conv2DTranspose(1, 3, padding='same', activation='sigmoid')
def call(self, z):
x = self.fc(z)
x = self.reshape(x)
x = self.h1(x)
x = self.h2(x)
x = self.output_layer(x)
return x
""" beta-VAE """
class betaVAE(Model):
def __init__(self, latent_dim):
super(betaVAE, self).__init__()
self.latent_dim = latent_dim
self.encoder = Encoder(latent_dim)
self.decoder = Decoder()
def call(self, x):
mu, log_var = self.encoder(x)
encoded = self.reparameterize(mu, log_var)
decoded = self.decoder(encoded)
return decoded, encoded, mu, log_var
def reparameterize(self, mu, log_var):
epsilon = tf.random.normal(shape=tf.shape(mu))
return epsilon * tf.exp(0.5*log_var) + mu
if __name__ == "__main__":
a = betaVAE(2)
a.build(input_shape=(None, 28,28,1))
a.encoder.summary()
a.decoder.summary()
vae_train.py
# beta-VAE model for MNIST
# coded by st.watermelon
import os
import tensorflow as tf
from tensorflow.keras.models import Model
from vae_model import betaVAE
import matplotlib.pyplot as plt
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "2"
""" loading training and test data """
def get_data():
mnist = tf.keras.datasets.mnist
(x_train, _), (x_test, _) = mnist.load_data()
# adjusting to 0 ~ 1.0
x_train = x_train / 255.0
x_test = x_test / 255.0
# reshaping
x_train = x_train.reshape(-1,28,28,1)
x_test = x_test.reshape(-1,28,28,1)
return x_train, x_test
""" setup beta-VAE agent """
class betaVAEagent(Model):
def __init__(self, latent_dim, beta):
super(betaVAEagent, self).__init__()
self.latent_dim = latent_dim
self.beta = beta
self.beta_vae = betaVAE(latent_dim)
self.beta_vae.build(input_shape=(None, 28, 28, 1)) # (batch, H, W, C)
lr = 1e-3
self.optimizer = tf.keras.optimizers.Adam(learning_rate=lr)
def loss_function(self, x):
x_hat, z, mu, log_var = self.beta_vae(x)
recons_loss = tf.reduce_mean(
tf.reduce_sum(
#tf.keras.losses.binary_crossentropy(x, x_hat), axis=(1, 2)
tf.keras.losses.MSE(x, x_hat), axis=(1, 2)
)
)
kl_loss = -0.5 * (1 + log_var - tf.square(mu) - tf.exp(log_var))
kl_loss = tf.reduce_mean(tf.reduce_sum(kl_loss, axis=1))
loss = recons_loss + self.beta * kl_loss
return loss, recons_loss, kl_loss
def train_step(self, x):
with tf.GradientTape() as tape:
loss, recons_loss, kl_loss = self.loss_function(x)
gradients = tape.gradient(loss, self.trainable_variables)
self.optimizer.apply_gradients(zip(gradients, self.trainable_variables))
return {'total_loss': loss, 'recons_loss': recons_loss, 'kl_loss': kl_loss}
def save_weights(self):
self.beta_vae.save_weights("./save_weights/vae.h5")
def train(self, train_dataset, epochs):
train_loss_history = []
kl_loss_history = []
recons_loss_history = []
for epoch in range(1, epochs + 1):
print(f"Epoch {epoch}/{epochs}")
epoch_train_loss = []
epoch_kl_loss = []
epoch_recons_loss = []
for step, batch in enumerate(train_dataset):
loss_dict = self.train_step(batch)
epoch_train_loss.append(loss_dict['total_loss'].numpy())
epoch_recons_loss.append(loss_dict['recons_loss'].numpy())
epoch_kl_loss.append(loss_dict['kl_loss'].numpy())
if step % 100 == 0:
loss = loss_dict['total_loss']
recons_loss = loss_dict['recons_loss']
kl_loss = loss_dict['kl_loss']
print(f"Step {step}, Total Loss: {loss}, Recon Loss: {recons_loss}, KL Loss: {kl_loss}")
train_loss_history.append(tf.reduce_mean(epoch_train_loss))
kl_loss_history.append(tf.reduce_mean(epoch_kl_loss))
recons_loss_history.append(tf.reduce_mean(epoch_recons_loss))
# Save encoder and decoder weights after each epoch
self.save_weights()
# plot loss history
plt.plot(train_loss_history, label='Training Loss')
plt.plot(kl_loss_history, label='KL Loss')
plt.plot(recons_loss_history, label='Recons Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.show()
def main():
x_train, _ = get_data()
train_size = x_train.shape[0]
batch_size = 128
train_dataset = (tf.data.Dataset.from_tensor_slices(x_train)
.shuffle(train_size).batch(batch_size))
latent_dim = 2
beta = 1
agent = betaVAEagent(latent_dim, beta)
epochs = 30
agent.train(train_dataset, epochs)
if __name__ == "__main__":
main()
'AI 딥러닝 > DLA' 카테고리의 다른 글
| [YOLO] 욜로의 진화 (0) | 2025.07.11 |
|---|---|
| [PINN] PINN을 이용한 램버트 문제의 해 (0) | 2024.04.10 |
| [VAE] 변이형 오토인코더(Variational Autoencoder) (0) | 2023.04.30 |
| [U-Net] 망막 혈관 세그멘테이션 (Retinal Vessel Segmentation) (0) | 2022.05.11 |
| [U-Net] U-Net 구조 (0) | 2022.05.11 |




댓글