생성모델(generative model)은 데이터를 생성해 낼 수 있는 모델을 말한다.
만약 데이터의 확률분포 \(-\) 데이터가 이산적일 경우는 확률질량함수(probability mass function), 연속적일 경우는 확률밀도함수(probability density function) \(-\) 를 알 수 있으면 샘플링을 통해서 본래 데이터와 같은 확률적 특성을 갖는 새로운 데이터를 임의로 생성할 수 있으므로, 생성모델의 목적은 데이터의 확률분포를 추정하는 것이라고 말할 수 있다. 예를 들면 데이터로서 얼굴 이미지 집합이 주어졌을 때, 그 이미지의 특성을 나타내는 확률밀도함수를 추정할 수 있다면, 새로운 얼굴 이미지를 임의로 생성할 수 있다는 말이다.

생성모델은 고차원(high dimension) 데이터가 저차원(low dimension)의 잠재변수(latent variable)에 의해서 생성된다고 가정한다. 즉, 복잡다단한 세상의 물리적 현상들이 간단한 자연법칙에 의해 지배되고 있다고 생각하는 것과 같은 원리이다. 예를 들어 \(128 \times 128\) 의 다양한 이미지(\(128 \times 128=16,384\) 차원의 벡터)도 이보다 훨씬 차원이 낮은 미지의 잠재변수의 함수로 생성시킬 수 있다고 가정하는 것이다. 보통 데이터는 명목상 고차원이지만 저차원의 매니폴드 주변에 집중되어 분포하는 경우가 많다는데 착안한 가정이라고 볼 수 있다.
만약 이런 가정이 성립한다면, 데이터를 기반으로 어떤 분류를 수행한다고 할 때, 고차원의 데이터 대신에 저차원의 잠재변수 기반으로 분류를 수행할 수도 있고, 데이터를 만든 어떤 보이지 않는 원인 등을 저차원 잠재변수를 이용하여 해석할 수도 있다. 또한 가장 중요한 장점인데, 잠재변수를 이용하여 본래 데이터와 같은 확률분포를 갖는 새로운 데이터를 생성시킬 수도 있다.
최근 심층 신경망을 이용한 생성모델의 연구와 응용이 폭발적으로 증가하여 이미지, 텍스트, 음성은 물론 영상까지 생성하고 있으며 다양한 관련 서비스들이 상업화되고 있다. 뿐만 아니라 물리 시스템을 다루는 전통적인 학문 분야, 예를 들면 항공우주분야에까지 생성모델이 도입되어 고장진단, 역설계 최적화, 항공교통관리를 위한 항적 생성 등의 문제에서 탁월한 성과를 내고 있다.
여러가지 생성모델 중 VAE(variational autoencoder, 변이형 오토인코더)가 특히 물리 시스템에 관한 생성모델로서 많이 사용되고 있으므로 이에 대해 알아보기로 하자.
확률의 관점에서 생성모델 문제를 수학적으로 풀어보면 다음과 같다. 우선 데이터를 \(\mathbf{x}\), 잠재변수를 \(\mathbf{z}\), 데이터의 확률밀도함수를 \(p(\mathbf{x})\), 잠재변수의 확률밀도함수를 \(p(\mathbf{z})\), 잠재변수를 조건으로 하는 데이터의 조건부 확률밀도함수를 \(p(\mathbf{x}| \mathbf{z})\) 라고 하면, 생성모델 문제는 데이터의 확률밀도함수 \(p(\mathbf{x})\) 를 추정하는 것이다.
문제는 어떻게 \(p(\mathbf{x})\) 를 추정할 수 있는냐 하는 것인데, 우선 베이즈(Bayes) 정리를 이용하여 각 확률밀도함수 간의 관계식을 살펴보자.
\[ p(\mathbf{x})= \frac{p(\mathbf{x} \vert \mathbf{z}) p(\mathbf{z})}{p(\mathbf{z} \vert \mathbf{x})} \tag{1} \]
여기서 잠재변수의 확률밀도함수 \(p(\mathbf{z})\) 는 일종의 설계변수로 볼 수 있기 때문에 보통 정규분포로 즉, \(p(\mathbf{z})=\mathcal{N}(0,I)\) 로 가정한다. \(p(\mathbf{z} \vert \mathbf{x})\) 는 데이터가 주어졌을 때의 잠재변수의 확률분포인데 데이터를 잠재변수의 공간으로 표현하기 때문에 인코더(encoder, 암호기)라고 볼 수 있다. 한편으로는 복잡한 현상에 숨은 간단한 원인을 파헤치는 것이기도 하므로 추론(inference) 과정이라고도 한다.
반대로 \(p(\mathbf{x} \vert \mathbf{z})\) 는 잠재변수를 데이터의 공간으로 구현하는 것이기 때문에 디코더(decoder, 복호기)라고 볼 수 있다 한편으로는 숨은 원인을 이용하여 복잡한 현상을 구현하는 것이기도 하므로 생성기(generator)라고도 한다.

\( p(\mathbf{z} \vert \mathbf{x})\) 는 매우 복잡한 확률분포를 가질 수 있고 직접 추정이 어려우므로 파라미터 \(\phi\) 로 표현되는 확률밀도함수 \(q_\phi (\mathbf{z} \vert \mathbf{x})\) 로 \(p(\mathbf{z} \vert \mathbf{x})\) 를 근사화 하는 방법으로 접근한다. 확률밀도함수 \(q_\phi (\mathbf{z} \vert \mathbf{x})\) 는 가우시안이나 그 밖의 다루기 쉬운 확률분포로 가정한다.
두 확률밀도함수가 서로 얼마나 유사한지를 측정하는 수단으로는 KL(Kullback-Leibler, 쿨백-라이블러)발산을 사용하기로 한다. 그러면 두 함수의 KL은 다음과 같다.
\[ \begin{align} \mathbb{KL} \left(q_\phi (\mathbf{z} \vert \mathbf{x}) \Vert p(\mathbf{z} \vert \mathbf{x}) \right) &= \int q_\phi (\mathbf{z} \vert \mathbf{x}) \log \frac{q_\phi (\mathbf{z} \vert \mathbf{x}) }{ p( \mathbf{z} \vert \mathbf{x}) } \ d\mathbf{z} \tag{2} \\ \\ &= \int q_\phi (\mathbf{z} \vert \mathbf{x}) \log \frac{q_\phi (\mathbf{z} \vert \mathbf{x}) p(\mathbf{x})}{ p( \mathbf{x}, \mathbf{z}) } \ d\mathbf{z} \end{align} \]
위 식은 \(q_\phi (\mathbf{z} \vert \mathbf{x})\) 로 계산하는 \(\log\) 함수의 기댓값이기 때문에 다음과 같이 쓸 수 있다.
\[ \begin{align} \mathbb{KL} \left(q_\phi (\mathbf{z} \vert \mathbf{x}) \Vert p(\mathbf{z} \vert \mathbf{x}) \right) &= \mathbb{E}_q \left[ \log \frac{q_\phi (\mathbf{z} \vert \mathbf{x}) p(\mathbf{x})}{ p(\mathbf{x}, \mathbf{z})} \right] \tag{3} \\ \\ &= \mathbb{E}_q [ \log q_\phi (\mathbf{z} \vert \mathbf{x} ) ]+ \log p(\mathbf{x}) - \mathbb{E}_q [ \log p(\mathbf{x}, \mathbf{z} ) ] \end{align} \]
여기서 \( \mathbb{E}_q [ \log p(\mathbf{x}, \mathbf{z} ) ] \) 를 제거하기 위하여 다음 관계식을 살펴보자.
\[ \begin{align} \log p(\mathbf{x}, \mathbf{z}) &= \log p(\mathbf{x} \vert \mathbf{z}) p(\mathbf{z}) \tag{4} \\ \\ &= \log \frac{q_\phi (\mathbf{z} \vert \mathbf{x})p( \mathbf{x} \vert \mathbf{z})p(\mathbf{z} ) }{ q_\phi (\mathbf{z} \vert \mathbf{x} )} \\ \\ &= \log \frac{p(\mathbf{z})}{q_\phi (\mathbf{z} \vert \mathbf{x}) } +\log q_\phi (\mathbf{z} \vert \mathbf{x} ) + \log p(\mathbf{x} \vert \mathbf{z} ) \end{align} \]
따라서 \( \mathbb{E}_q [ \log p(\mathbf{x}, \mathbf{z} ) ] \) 는 다음과 같이 쓸 수 있다.
\[ \begin{align} \mathbb{E}_q [ \log p(\mathbf{x}, \mathbf{z} ) ] &= -\int q_\phi (\mathbf{z} \vert \mathbf{x}) \log \frac{q_\phi (\mathbf{z} \vert \mathbf{x}) }{p(\mathbf{z})} \ d\mathbf{z} \tag{5} \\ \\ & \ \ \ \ \ \ \ \ \ \ + \mathbb{E}_q [ \log q_\phi (\mathbf{z} \vert \mathbf{x} ) ] + \mathbb{E}_q [ \log p(\mathbf{x} \vert \mathbf{z} ) ] \\ \\ &= - \mathbb{KL} \left( q_\phi (\mathbf{z} \vert \mathbf{x} ) \Vert p(\mathbf{z}) \right) \\ \\ & \ \ \ \ \ \ \ \ \ \ + \mathbb{E}_q [ \log q_\phi (\mathbf{z} \vert \mathbf{x}) ]+ \mathbb{E}_q [ \log p(\mathbf{x} \vert \mathbf{z}) ] \end{align} \]
식 (5)를 식 (3)에 대입하면 \(\log p(\mathbf{x}) \) 는 다음과 같이 된다.
\[ \begin{align} \log p(\mathbf{x}) &= \mathbb{KL} \left( q_\phi (\mathbf{z} \vert \mathbf{x}) \Vert p(\mathbf{z} \vert \mathbf{x}) \right) - \mathbb{KL} \left( q_\phi (\mathbf{z} \vert \mathbf{x}) \Vert p(\mathbf{z}) \right) \tag{6} \\ \\ & \ \ \ \ \ \ \ \ \ \ + \mathbb{E}_q [ \log p(\mathbf{x} \vert \mathbf{z} ) ] \end{align} \]
위 식의 오른쪽 항에서 첫 번째 항은 \(p(\mathbf{z} \vert \mathbf{x})\) 를 알 수 없으므로 계산할 수 없다. 하지만 KL은 항상 \(0\) 보다 크거나 같다는 사실을 이용하면 위 식은 다음과 같이 된다.
\[ \log p(\mathbf{x}) \ge - \mathbb{KL} \left( q_\phi (\mathbf{z} \vert \mathbf{x}) \Vert p(\mathbf{z}) \right) + \mathbb{E}_q [ \log p(\mathbf{x} \vert \mathbf{z} ) ] \tag{7} \]
즉, \(\log p(\mathbf{x}) \) 를 정확히 계산할 순 없지만 그 하한값(ELBO, evidence lower bound term)은 계산할 수 있다. 만약 하한값을 최대로 키우는 파라미터 \(\phi\) 를 구한다면, 오차 \(\mathbb{KL} \left( q_\phi (\mathbf{z} \vert \mathbf{x}) \Vert p(\mathbf{z} \vert \mathbf{x}) \right)\) 범위의 정확도로 \(\log p(\mathbf{x}) \) 를 추정할 수 있게 된다.
이제 \(p(\mathbf{x})\) 를 추정하는 문제를 다음 최적화 문제로 변경시킬 수 있다.
\[ \arg \max_\phi \mathbb{E}_q [ \log p(\mathbf{x} \vert \mathbf{z}) ]- \mathbb{KL} \left( q_\phi (\mathbf{z} \vert \mathbf{x} ) \Vert p(\mathbf{z}) \right) \tag{8} \]
\(p(\mathbf{z} \vert \mathbf{x})\) 를 파라미터 \(\phi\) 로 표현되는 확률밀도함수 \(q_\phi (\mathbf{z} \vert \mathbf{x})\) 로 근사화 했듯이 \(p(\mathbf{x} \vert \mathbf{z})\) 도 파라미터 \(\theta\) 로 표현되는 확률밀도함수 \(p_\theta (\mathbf{x} \vert \mathbf{z})\) 로 근사화한다. 그러면 위 최적화 문제는 다음과 같다.
\[ \arg \max_{\phi, \theta} \mathbb{E}_q [ \log p_\theta (\mathbf{x} \vert \mathbf{z}) ]- \mathbb{KL} \left( q_\phi (\mathbf{z} \vert \mathbf{x} ) \Vert p(\mathbf{z}) \right) \tag{9} \]
\(p_\theta (\mathbf{x} \vert \mathbf{z})\) 는 데이터의 종류에 따라서 베르누이 분포 또는 가우시안 분포로 모델링한다. 위 식의 첫 번째 항은 \(q_\phi (\mathbf{z} \vert \mathbf{x})\) 를 이용하여 계산하는 \(\log p_\theta (\mathbf{x} \vert \mathbf{z}) \) 의 기댓값으로서, \(q_\phi (\mathbf{z} \vert \mathbf{x})\) 로부터 \(\mathbf{z}^{(i)}\) 를 샘플링하고 그것을 기반으로 하여 \(\log p_\theta (\mathbf{x} \vert \mathbf{z}) \) 의 평균을 구한다. 즉, 전체 데이터 포인트 \(m\) 개 대해서 다음과 같이 평균을 구하면 된다.
\[ \begin{align} & \mathbb{E}_q [ \log p_\theta (\mathbf{x} \vert \mathbf{z}) ] \approx \frac{1}{m} \sum_i^m \log p_\theta (\mathbf{x} \vert \mathbf{z}^{(i) } ) \tag{10} \\ \\ & \mathbf{z}^{(i) } \sim q_\phi (\mathbf{z} \vert \mathbf{x} ) \end{align} \]
식 (9)에서 첫번째 항은 인코더(encoder)의 확률분포에 따라서 샘플링된 값을 기반으로 디코더(decoder)의 확률분포의 평균값을 구하는 것이기 때문에, 이 값을 최대로 한다는 의미는 로그-우도함수(log-likelihood)를 최대로 한다는 것이며, 이는 데이터의 확률분포를 베르누이로 가정했을 시에는 교차 엔트로피를 최소로 하는 것과 동일하고, 데이터 분포를 가우시안으로 가정했을 시에는 L2 놈(norm)을 최소로 하는 것과 동일하다. 또한 오토인코더(AE, autoencoder) 관점에서 보면 입력 데이터와 출력 데이터의 차이인 복원손실(reconstruction loss)을 최소로 한다는 것과 동일하다.
식 (9)에서 두번째 항은 인코더(encoder) 부분의 손실함수 항으로서 정규화 항(regularization term)이라고 하는데 잠재변수의 확률밀도함수 \(p(\mathbf{z})\) 와 파라미터 \(\phi\) 로 표현되는 확률밀도함수 \(q_\phi (\mathbf{z} \vert \mathbf{x})\) 가 같을 때 최소가 된다. 따라서 \(p(\mathbf{z})\) 를 정규분포로 정했기 때문에 \(q_\phi (\mathbf{z} \vert \mathbf{x})\) 도 정규분포가 되도록 파라미터 \(\phi\) 를 구하는 것이 필요하다. \(q_\phi (\mathbf{z} \vert \mathbf{x})\) 를 정규분포가 되도록 만든다는 의미는 데이터를 입력으로 받았을 때 나타나는 잠재변수의 분포를 정규분포가 되도록 파라미터 \(\phi\) 를 계산한다는 것이다.
\(q_\phi (\mathbf{z} \vert \mathbf{x})\) 를 평균이 \(\mu (\mathbf{x})\), 공분산 대각행렬이 \(\Sigma (\mathbf{x})\) 인 \(q_\phi (\mathbf{z} \vert \mathbf{x})= \mathcal{N}( \mu , \Sigma)\) 로 놓으면, 두 개의 가우시안 분포함수의 KL발산은 다음과 같이 해석적으로 계산할 수 있다.
\[ \begin{align} \mathbb{KL} \left( q_\phi (\mathbf{z} \vert \mathbf{x}) \Vert p(\mathbf{z}) \right) &= \mathbb{KL} ( \mathcal{N}(\mu, \Sigma) \Vert \mathcal{N}(0, I) ) \tag{11} \\ \\ &= \frac{1}{2} \left( tr(\Sigma )+ \mu^T \mu -k + \log \frac{1}{det \Sigma} \right) \\ \\ &=\frac{1}{2} \left( tr(\Sigma)+\mu^T \mu - k - \log \prod_j^k \Sigma_{jj} \right) \\ \\ &=\frac{1}{2} \sum_j^k \left( \Sigma_{jj}+ \mu_j^2-1-\log \Sigma_{jj} \right) \end{align} \]
여기서 \(k\) 는 잠재변수 \(\mathbf{z}\) 의 차원이다. \(\Sigma_{jj}\) 는 공분산 대각 행렬의 대각요소이다. 공분산 행렬의 대각요소는 분산이므로 편의상 \(\Sigma_{jj}= \sigma_j^2\) 로 표기하도록 한다. 위 최적화 문제는 전통적인 오토인코더(AE) 문제의 확률론적 변형에 해당하므로 VAE(variational autoencoder)라고 한다.
VAE 최적화 문제를 신경망을 이용하여 해를 구한다고 하면 신경망에서 최소화해야 할 손실함수는 다음과 같이 복원손실 항과 정규화 항으로 구성된다.
\[ \mathcal{L}= -\frac{1}{m} \sum_i^m \log p_\theta (\mathbf{x} \vert \mathbf{z}^{(i) } ) +\frac{1}{2} \sum_j^k (\sigma_j^2+ \mu_j^2-1-\log \sigma_j^2 ) \tag{12} \]
전체적인 신경망 모델의 개략적인 그림은 다음과 같다.
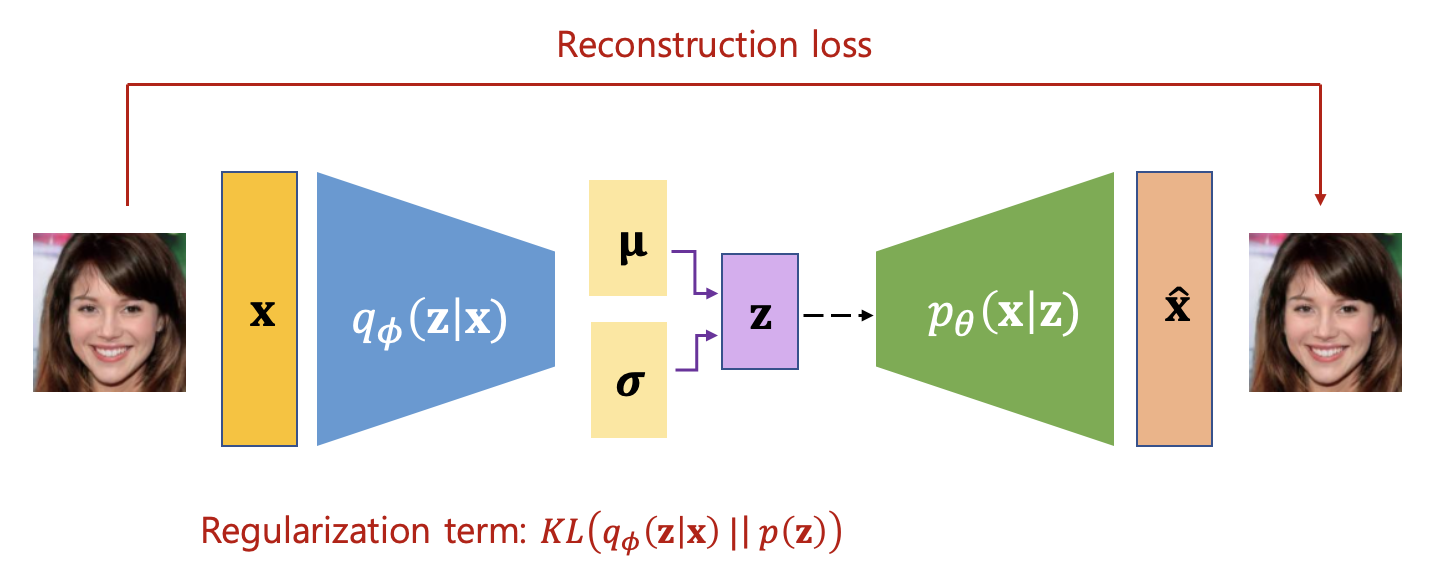
위 그림의 왼쪽부분은 인코더(encoder)로 고차원 입력 데이터를 정규분포를 갖는 저차원 잠재변수의 공간으로 인코딩하는 부분이다. 실제 데이터를 입력받아 인코더를 거쳐 잠재변수의 평균과 대각행렬인 공분산을 계산하며, 이것이 얼마나 정규분포와 유사한지가 인코더의 손실함수가 된다. 점선 부분은 샘플링을 의미한다.
오른쪽 부분은 디코더(decoder) 또는 생성기(generator)로 잠재변수를 샘플링한 값을 입력받아서 데이터를 복원하며, 이것이 입력된 데이터와 얼마나 유사한지를 나타내는 복원손실이 디코더의 손실함수가 된다.
한편, 손실함수가 최소가 되도록 최적화를 수행해야 하는데 샘플링 부분은 미분가능 하지 않으므로, 재 파라미터화(reparametrizing)라는 트릭을 사용한다. 즉, 평균이 \(\mu_j\), 분산이 \(\sigma_j^2\) 인 가우시안 분포에서 \(z_j\) 를 샘플링 한 것이나, \(z_j=\mu_j+\sigma_j \epsilon_j\) 이라 놓고 \(\epsilon_j\) 를 정규분포 \(\mathcal{N}(0, 1)\) 에서 샘플링한 것이나 \(z_j\) 의 확률적 특성은 동일하다는 사실을 이용하는 것이다. 재 파라미터화를 이용하면 샘플링 과정을 신경망의 외부에 위치시킬 수 있기 때문에, 신경망 학습시 미분가능하게 된다.
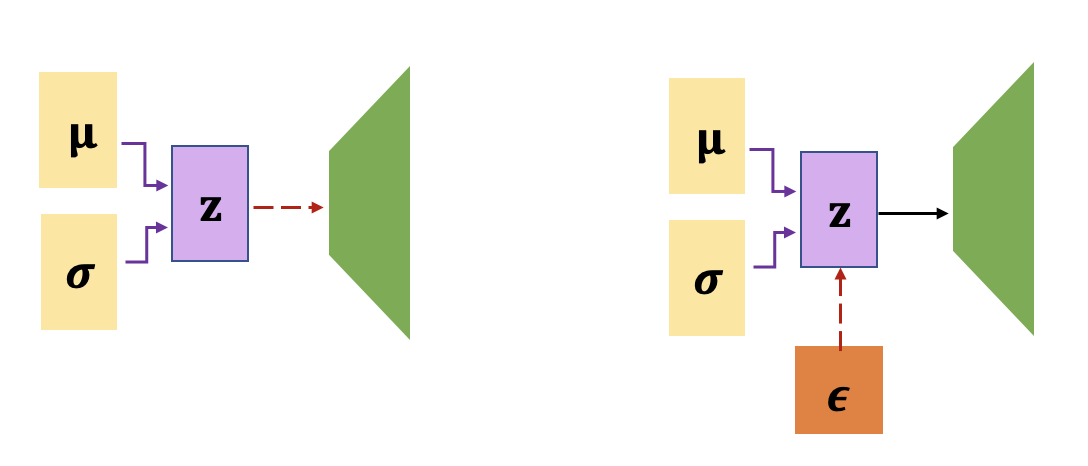
학습이 끝나고, 새로운 데이터를 발생시키는 단계에서는 \(\mathbf{z}\) 를 정규분포 \(\mathcal{N}(0, I)\) 에서 샘플링 하고 디코더(decoder)의 입력으로 넣어주면 된다.
'AI 딥러닝 > DLA' 카테고리의 다른 글
| [LLM] Ollama Web-UI 설치 (0) | 2024.02.25 |
|---|---|
| [VAE] beta-VAE (0) | 2023.05.11 |
| [U-Net] 망막 혈관 세그멘테이션 (Retinal Vessel Segmentation) (0) | 2022.05.11 |
| [U-Net] U-Net 구조 (0) | 2022.05.11 |
| [CNN] 컨볼루션과 상관도 (0) | 2020.09.22 |




댓글