선형 시스템과 부분공간 (Subspace)

다음과 같이 상태변수의 선형 미분 방정식으로 표현되는 운동 방정식이 있다고 하자.

 

$$\begin{array}{}\text{(1)}& \dot{\mathbf{x}}=A\mathbf{x}\end{array}$$

 

여기서 $\mathbf{x}(t)\in {\mathbb{R}}^n$ 는 상태변수, $A\in {\mathbb{R}}^{n\times n}$ 는 상수 행렬이다.

 

 

이 시스템의 해는 다음과 같다.

 

$$\begin{array}{}\text{(2)}& \mathbf{x}(t)=e^{At}\mathbf{x}(0)\end{array}$$

 

이전 포스트에서는 행렬지수함수(matrix exponential) $e^{At}$ 의 계산에 대해서 알아보았다 (https://pasus.tistory.com/233). 시스템 (1)의 운동 특성은 행렬 $A$ 의 고유값과 고유벡터에 따라 달라진다. 먼저 행렬 $A$ 가 서로 다른 $n$ 개의 고유값 ${\lambda }_1,{\lambda }_2,...,{\lambda }_n\in \mathbb{C}$ 를 갖는 경우에 대해서 알아본다.

고유값 ${\lambda }_1,{\lambda }_2,...,{\lambda }_n$ 에 대응하는 고유벡터를 ${\mathbf{v}}_1,{\mathbf{v}}_2,...,{\mathbf{v}}_n$ 이라고 하면 식 (2)는 다음과 같이 쓸 수 있다.

 

$$\begin{array}{}\text{(3)}& \mathbf{x}(t)=[{\mathbf{v}}_1{\mathbf{v}}_2\cdots {\mathbf{v}}_n]\left[\begin{array}{cccc}{e}^{{\lambda }_{1}t}& & & \\ & e^{{\lambda }_{2}t}& & \\ & & \ddots & \\ & & & e^{{\lambda }_{n}t}\end{array}\right][{\mathbf{v}}_1{\mathbf{v}}_2\cdots {\mathbf{v}}_n{]}^{-1}\mathbf{x}(0)\end{array}$$

 

여기서 초기값 $\mathbf{x}(0)$ 를 고유벡터의 선형 조합으로 표현하고

 

$$\begin{array}{r}\text{(4)}& \mathbf{x}(0)& =c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+\cdots +c_n{\mathbf{v}}_n\\ & =[{\mathbf{v}}_1{\mathbf{v}}_2\cdots {\mathbf{v}}_n]\left[\begin{array}{c}{c}_1\\ c_2\\ ⋮\\ c_n\end{array}\right]\end{array}$$

 

이를 식 (3)에 대입하면 시스템의 해는 다음과 같이 된다.

 

$$\begin{array}{}\text{(5)}& \mathbf{x}(t)=c_1{e}^{{\lambda }_{1}t}{\mathbf{v}}_1+c_2{e}^{{\lambda }_{2}t}{\mathbf{v}}_2+\cdots +c_n{e}^{{\lambda }_{n}t}{\mathbf{v}}_n\end{array}$$

 

만약 고유값이 복소수라면 고유값과 고유벡터를 실수화하는 것이 편리하다. 예를 들어 고유값 ${\lambda }_1,{\lambda }_2$ 와 고유벡터 ${\mathbf{v}}_1,{\mathbf{v}}_2$ 가 다음과 같이 켤레복소수로 주어진다면,

 

$${\lambda }_{1,2}=\sigma \pm j\omega ,{\mathbf{v}}_{1,2}={\mathbf{v}}_R\pm j{\mathbf{v}}_I$$

 

식 (2)는 다음과 같이 쓸 수 있다.

 

$$\begin{array}{r}\text{(6)}& \mathbf{x}(t)& =[{\mathbf{v}}_R{\mathbf{v}}_I\cdots {\mathbf{v}}_n]\left[\begin{array}{cccc}{e}^{\sigma t}\cos (\omega t)& e^{\sigma t}\sin (\omega t)& & \\ -e^{\sigma t}\sin (\omega t)& e^{\sigma t}\cos (\omega t)& & \\ & & \ddots & \\ & & & e^{{\lambda }_{n}t}\end{array}\right]\\ & [{\mathbf{v}}_R{\mathbf{v}}_I\cdots {\mathbf{v}}_n{]}^{-1}\mathbf{x}(0)\end{array}$$

 

그러면 식 (5)도 다음과 같이 바뀌게 된다.

 

$$\begin{array}{r}\text{(7)}& \mathbf{x}(t)& =e^{\sigma t}(c_1\cos (\omega t)+c_2\sin (\omega t)){\mathbf{v}}_R\\ & +e^{\sigma t}(c_2\cos (\omega t)-c_1\sin (\omega t)){\mathbf{v}}_I+\cdots +c_n{e}^{{\lambda }_{n}t}{\mathbf{v}}_n\end{array}$$

 

만약 행렬 $A$ 의 고유값이 2개 이상의 중근(repeated eigenvalues)을 갖는다면 해당 고유값 ${\lambda }_m$ 에 대한 $nullity({\lambda }_{m}I-A)$ 에 따라 여러 형태의 조단 표준형을 갖는 해를 구할 수 있다. 예를 들어 고유값 ${\lambda }_1={\lambda }_2$ 이고 이에 대응하는 고유벡터가 ${\mathbf{v}}_1$, 일반화 고유벡터가 ${\mathbf{v}}_2$ 라면, 식 (2)는 다음과 같이 쓸 수 있다.

 

$$\begin{array}{}\text{(8)}& \mathbf{x}(t)=[{\mathbf{v}}_1{\mathbf{v}}_2\cdots {\mathbf{v}}_n]\left[\begin{array}{cccc}{e}^{{\lambda }_{1}t}& t{e}^{{\lambda }_{1}t}& & \\ & e^{{\lambda }_{1}t}& & \\ & & \ddots & \\ & & & e^{{\lambda }_{n}t}\end{array}\right][{\mathbf{v}}_1{\mathbf{v}}_2\cdots {\mathbf{v}}_n{]}^{-1}\mathbf{x}(0)\end{array}$$

 

그러면 식 (5)도 다음과 같이 바뀌게 된다.

 

$$\begin{array}{}\text{(9)}& \mathbf{x}(t)=(c_1+c_{2}t)e^{{\lambda }_{1}t}{\mathbf{v}}_1+c_2{e}^{{\lambda }_{1}t}{\mathbf{v}}_2+\cdots +c_n{e}^{{\lambda }_{n}t}{\mathbf{v}}_n\end{array}$$

 

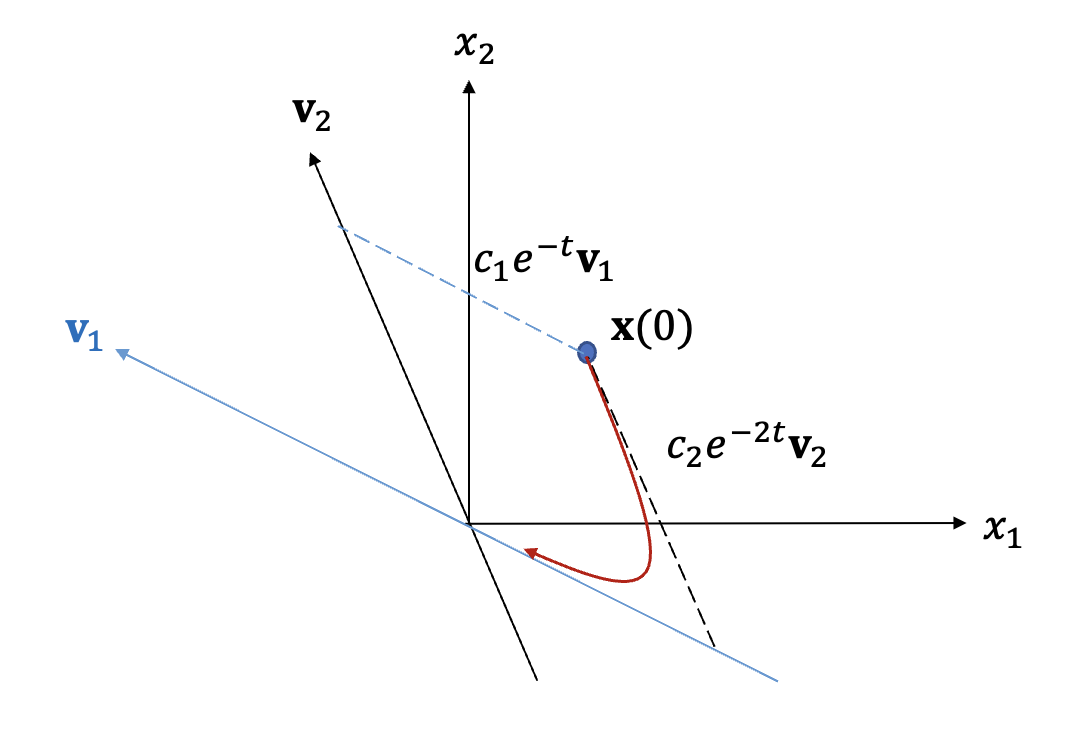
식 (5), (6), (7)에서 만약 초기값 $\mathbf{x}(0)$ 가 특정 부분공간에서 시작했다면, 예를 들어 $\mathbf{x}(0)=c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2$ 이면, $\mathbf{x}(t)$ 도 상황에 따라서 각각 다음과 같이 되어서

 

$$\begin{array}{rl}& \mathbf{x}(t)=c_1{e}^{{\lambda }_{1}t}{\mathbf{v}}_1+c_2{e}^{{\lambda }_{2}t}{\mathbf{v}}_2\\ \\ & \mathbf{x}(t)=e^{\sigma t}(c_1\cos (\omega t)+c_2\sin (\omega t)){\mathbf{v}}_1+e^{\sigma t}(c_2\cos (\omega t)-c_1\sin (\omega t)){\mathbf{v}}_2\\ \\ & \mathbf{x}(t)=(c_1+c_{2}t)e^{{\lambda }_{1}t}{\mathbf{v}}_1+c_2{e}^{{\lambda }_{1}t}{\mathbf{v}}_2\end{array}$$

 

해당 특정 부분공간에 남아 있게 된다.

 

 

$A$ 의 고유값 중에서 실수부가 음수인 고유값에 해당하는 (일반화)고유벡터 집합을 $\{{\mathbf{v}}_1,...,{\mathbf{v}}_s\}$ 로 표시하고, 실수부가 양수인 고유값에 해당하는 (일반화)고유벡터 집합을 $\{{\mathbf{v}}_{s+1},...,{\mathbf{v}}_{s+u}\}$ 로, 실수부가 $0$ 인 고유값에 해당하는 (일반화)고유벡터 집합을 $\{{\mathbf{v}}_{s+u+1},...,{\mathbf{v}}_{s+u+c}\}$ 로 표시한다면, $n$ 차원 벡터공간 ${\mathbb{R}}^n$ 은 다음으로 정의되는 ${\mathbb{E}}^s$, ${\mathbb{E}}^u$ 및 ${\mathbb{E}}^c$ 로 표시된 세개의 공간으로 분할할 수 있다.

 

$$\begin{array}{r}\text{(10)}& & {\mathbb{E}}^s=span\{{\mathbf{v}}_1,...,{\mathbf{v}}_s\}\\ & {\mathbb{E}}^u=span\{{\mathbf{v}}_{s+1},...,{\mathbf{v}}_{s+u}\}\\ \\ & {\mathbb{E}}^c=span\{{\mathbf{v}}_{s+u+1},...,{\mathbf{v}}_{s+u+c}\},s+u+c=n\end{array}$$

 

${\mathbb{E}}^s$, ${\mathbb{E}}^u$ 및 ${\mathbb{E}}^c$ 를 각각 안정 부분공간(stable subspace), 불안정(unstable) 부분공간 및 센터(center) 부분공간이라고 한다. 또한 불변(invariant) 부분공간 또는 불변 매니폴드(manifold, 다형체)라고도 한다. 불변인 이유는 초기값 $\mathbf{x}(0)$ 가 특정 부분공간에서 시작했다면 $\mathbf{x}(t),t\ge 0$ 도 해당 특정 부분공간에 영원히 남아 있기 때문이다.

특히 ${\mathbb{E}}^s$ 에서 시작하는 해 $\mathbf{x}(t)$ 는 $t\to +\mathrm{\infty }$ 일 때 점근적으로 $\mathbf{x}(t)=0$ 으로 접근하고, ${\mathbb{E}}^u$ 에서 시작하는 해는 $t\to -\mathrm{\infty }$ 일 때 점근적으로 $\mathbf{x}(t)=0$ 에 접근한다.

예를 들어 보자. 다음과 같은 시스템이 있다.

 

$$\begin{array}{}\text{(11)}& \dot{\mathbf{x}}=\left[\begin{array}{cc}0& 1\\ -2& -3\end{array}\right]\mathbf{x}\end{array}$$

 

고유값은 $({\lambda }_1,{\lambda }_2)=(-1,-2)$ 이고 고유벡터는 $[{\mathbf{v}}_1{\mathbf{v}}_2]=\left[\begin{array}{cc}1& 1\\ -1& -2\end{array}\right]$이다. 이 경우 ${\mathbb{E}}^s=span\{{\mathbf{v}}_1,{\mathbf{v}}_2\}$ 이다. 다양한 초기값에 대해서 $\mathbf{x}(t)$ 의 궤적을 그려보면 다음과 같다.

 

 

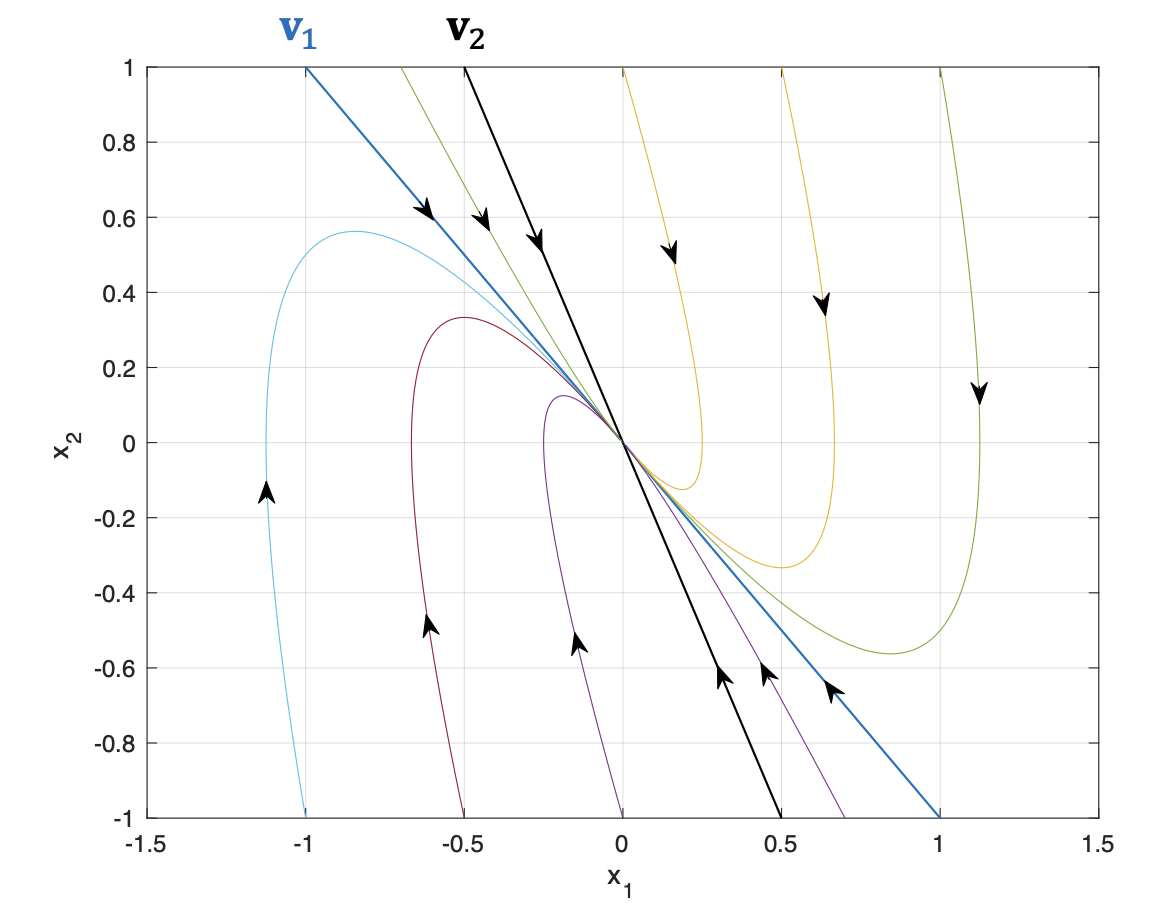
위 그림에 고유벡터의 방향이 표시되어 있다. 모드별로 수렴 속도에 차이가 있는데 ${\mathbf{v}}_1$ 은 $e^{-t}$ 로, ${\mathbf{v}}_2$ 는 $e^{-2t}$ 로서 수렴속도가 ${\mathbf{v}}_2$ 가 더 빠르다.

 

 

다른 예를 들어보자. 다음과 같은 시스템이 있다.

 

$$\begin{array}{}\text{(12)}& \dot{\mathbf{x}}=\left[\begin{array}{ccc}-1& 1& 0\\ -1& -1& 0\\ 0& 0& 1\end{array}\right]\mathbf{x}\end{array}$$

 

이 시스템의 고유값은 두 개의 결레복소수 ${\lambda }_{1,2}=-1\pm j1$ 과 한 개의 양의 실수 고유값 ${\lambda }_3=1$ 이고 실수화된 고유벡터는 $[{\mathbf{v}}_1{\mathbf{v}}_2{\mathbf{v}}_3]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$ 이다. 이 경우 ${\mathbb{E}}^s=span\{{\mathbf{v}}_1,{\mathbf{v}}_2\}$, ${\mathbb{E}}^u=span\{{\mathbf{v}}_3\}$ 이다. 다양한 초기값에 대해서 $\mathbf{x}(t)$ 의 궤적을 그려보면 다음과 같다.

 

 

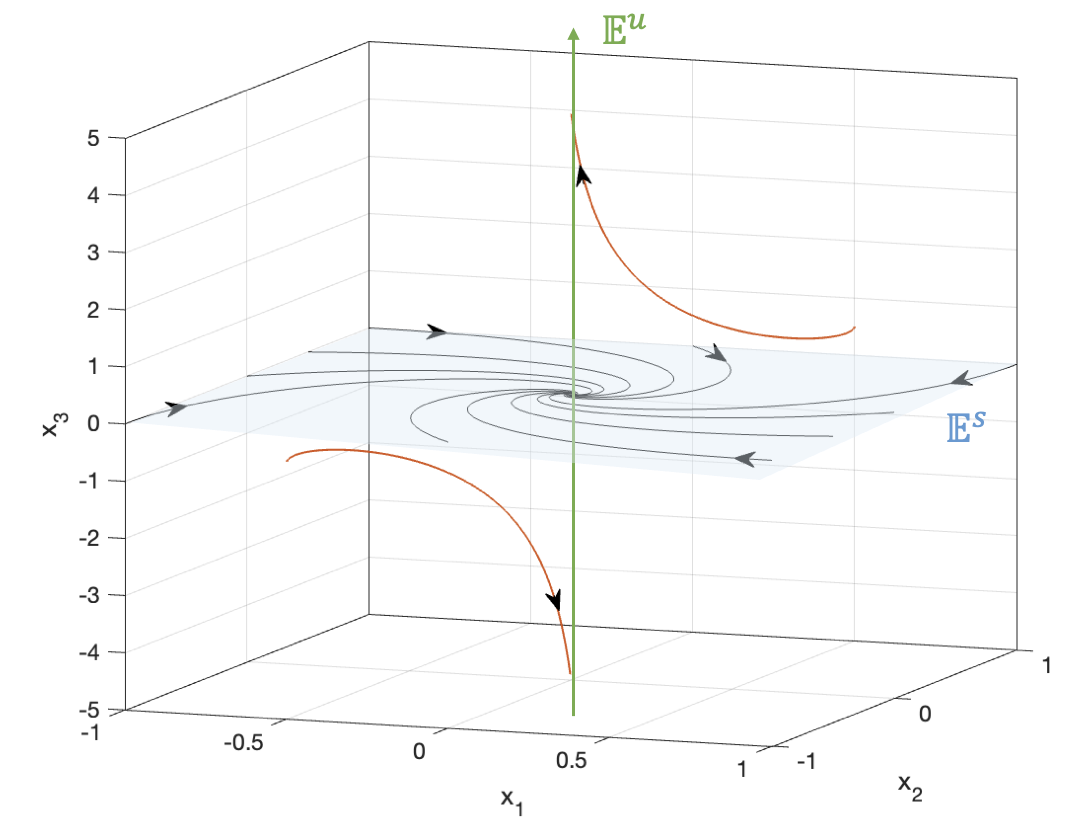
안정 부분공간 ${\mathbb{E}}^s$ 에서 출발한 궤적은 모두 $0$ 으로 수렴하는 반면, 그렇지 않은 궤적은 모두 불안정 부분공간인 ${\mathbb{E}}^u$, 즉 ${\mathbf{v}}_3$ 축을 따라서 무한대로 발산하는 것을 볼 수 있다.

마지막 예로 다음 시스템을 보자.

 

$$\begin{array}{}\text{(13)}& \dot{\mathbf{x}}=\left[\begin{array}{ccc}0& 1& 0\\ -4& 0& 0\\ 0& 0& -3\end{array}\right]\mathbf{x}\end{array}$$

 

이 시스템의 고유값은 두 개의 허수 ${\lambda }_{1,2}=\pm j2$ 와 한 개의 음의 실수 고유값 ${\lambda }_3=-3$ 이고 실수화된 고유벡터는 $[{\mathbf{v}}_1{\mathbf{v}}_2{\mathbf{v}}_3]=\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]$ 이다. 이 경우 ${\mathbb{E}}^c=span\{{\mathbf{v}}_1,{\mathbf{v}}_2\}$, ${\mathbb{E}}^s=span\{{\mathbf{v}}_3\}$ 이다. 다양한 초기값에 대해서 $\mathbf{x}(t)$ 의 궤적을 그려보면 다음과 같다.

 

 

궤적은 모두 안정 부분공간인 ${\mathbb{E}}^s$, 즉 ${\mathbf{v}}_3$ 축을 따라서 센터 부분공간인 ${\mathbb{E}}^c$, 즉 ${\mathbf{v}}_1$ 과 ${\mathbf{v}}_2$ 축으로 이루어진 평면으로 수렴하며, 결국 센터 부분공간에서 원점을 중심으로 하는 타원궤적이 되는 것을 볼 수 있다.