수학에서 자율 미분방정식(autonomous differential equation) 또는 자율 시스템은 명시적으로 독립변수의 함수가 아닌 미분방정식 또는 시스템을 말한다.
독립변수가 시간이라면 시불변(time-invariant) 시스템이라고도 한다. 독립변수가 시간인 비선형 비자율 미분방정식은 \(\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x}, t)\) 로, 자율 시스템 또는 시불변 시스템은 \(\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})\) 로 표기한다.
어떤 시불변 시스템 \(\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})\) 의 한 평형상태(equilibrium state)를 \(\mathbf{x}_e\) 라고 하자. 평형상태란 \(\dot{\mathbf{x}_e}=0=\mathbf{f}(\mathbf{x}_e)\) 의 상태를 말한다. 비선형 시스템에서 평형상태는 여러 개 존재할 수 있다.
먼저 리야프노프 안정성(Lyapunov stability)에 대해서 정의한다.
만약 \(\Vert \mathbf{x}(0)- \mathbf{x}_e \rVert \lt \delta \) 에 대해서, 모든 시간 \(t \ge 0\) 에서 \(\Vert \mathbf{x}(t)- \mathbf{x}_e \rVert \lt \epsilon \) 가 되도록 어떤 \(\epsilon \gt 0\) 값에 대해서도 이에 대응하는 \(\delta \gt 0\) 가 존재한다면, 평형상태 \(\mathbf{x}_e\) 는 안정(stable)하다고 정의한다. 그리고 이와 같은 정의를 리야프노프 안정성 정의라고 한다.
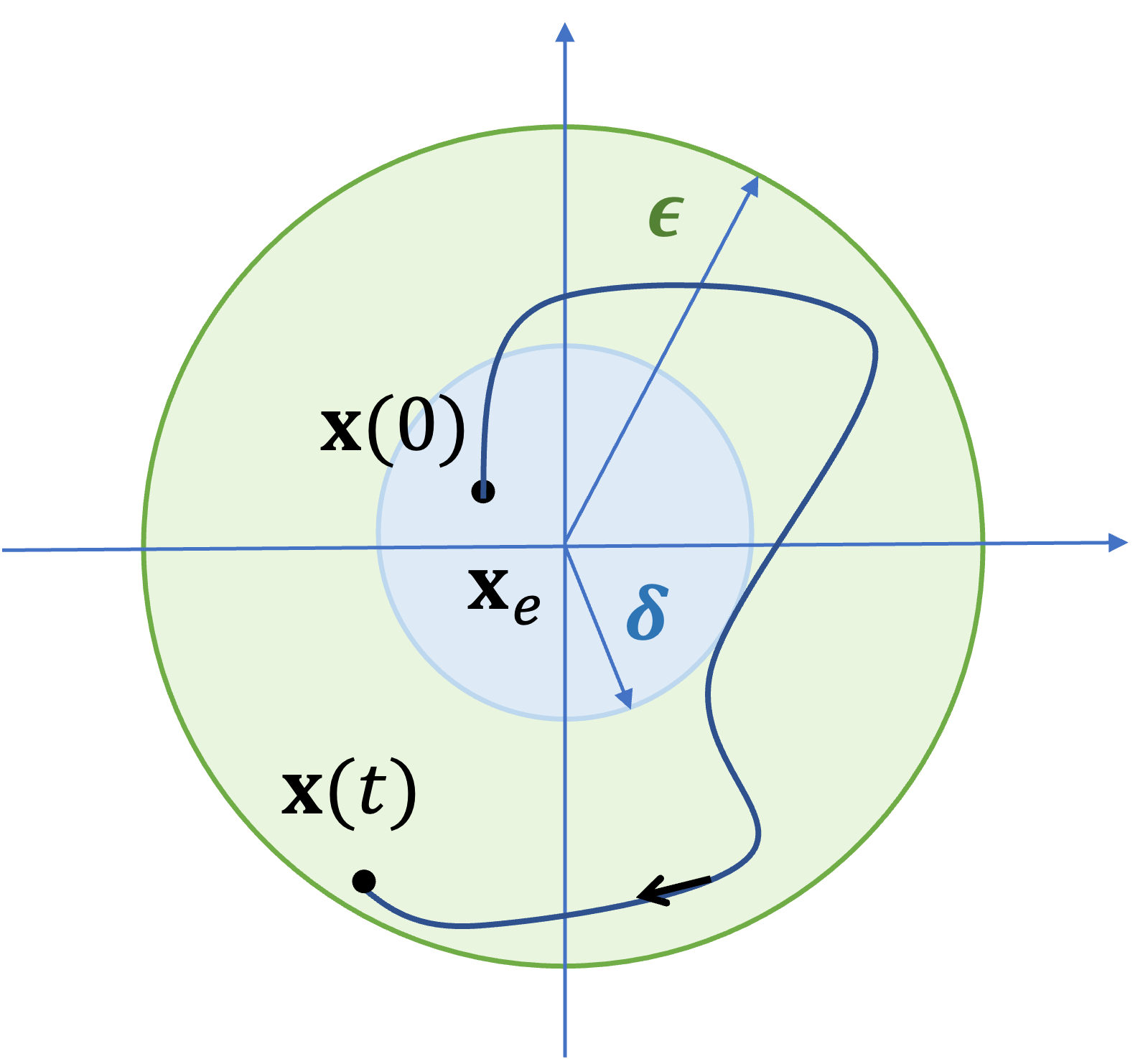
여기서 \(\mathbf{x}(0)\) 는 시간이 \(t=0\) 일 때의 상태변수값인 초기값을 말한다. \(\Vert \mathbf{x}(0)- \mathbf{x}_e \rVert \lt \delta \) 는 중심이 \(\mathbf{x}_e\) 이고 반지름이 \(\delta\) 인 원구(ball)의 내부에 \(\mathbf{x}(0)\) 가 위치해 있다는 의미이다. \(\Vert \mathbf{x}(t)- \mathbf{x}_e \rVert \lt \epsilon \) 는 중심이 \(\mathbf{x}_e\) 이고 반지름이 \(\epsilon\) 인 원구(ball)의 내부에 상태변수의 시간 궤적 \(\mathbf{x}(t)\) 가 머물고 있다는 의미이다.
리야프노프 안정성 정의에 의하면 \(\epsilon \gt 0\) 의 크기는 임의로 설정할 수 있고, 이에 대응하는 \(\delta \gt 0\) 가 존재해야 한다고 말한다. 즉, 리야프노프 안정성은 평형상태를 중심으로 임의의 크기로 설정한 영역(ball)안에 상태변수의 궤적을 머물게 만드는 상태변수 초기 위치가 평형상태를 중심으로 하는 일정 크기의 영역안에 항상 존재해야 함을 의미한다.
리야프노프 안정성의 정의를 수학 기호를 사용하여 컴팩트하게 표현하면 다음과 같다.
\[ \begin{align} & \forall \epsilon \gt 0, \ \exists \ \delta \gt 0 \ \ \mbox{such that } \\ \\ & \Vert \mathbf{x}(0)- \mathbf{x}_e \rVert \lt \delta \ \Rightarrow \ \forall t \ge 0, \ \Vert \mathbf{x}(t)- \mathbf{x}_e \rVert \lt \epsilon \end{align} \]
여기서 \(\forall\) 는 'for any' 또는 'for all', \(\exists\) 는 'there exists', \(\Rightarrow\) 는 'implies that' 을 뜻하는 기호다.
예를 들어서 다음과 같은 시스템이 있을 때,
\[ \dot{x} = x-x^3 \tag{1} \]
이 시스템의 평형상태는 \(x_e=0, \ 1, \ -1\) 등 3개다, 평형상태 \(0\) 은 불안정(unstable)하고, \(1\) 과 \(-1\) 은 안정하다.
만약 평형상태 \(\mathbf{x}_e\) 가 안정하고 시스템의 모든 해가 평형상태로 수렴하는, 즉 \(\lim_{t \to \infty} \mathbf{x}(t) = \mathbf{x}_e\) 가 되는 일정 범위 \( \lVert \mathbf{x}(0)- \mathbf{x}_e \rVert \lt \delta\) 가 존재한다면, 평형상태는 로컬(local)에서 점근적(asymptotic)으로 안정하다고 정의한다 (local asymptotic stability). 그리고 그 일정 범위 \( \lVert \mathbf{x}(0)- \mathbf{x}_e \rVert \lt \delta\) 를 수렴영역(region of attraction)이라고 한다. 이 영역에서 출발한 상태변수는 결국 평형상태로 끌려가듯이 수렴한다.
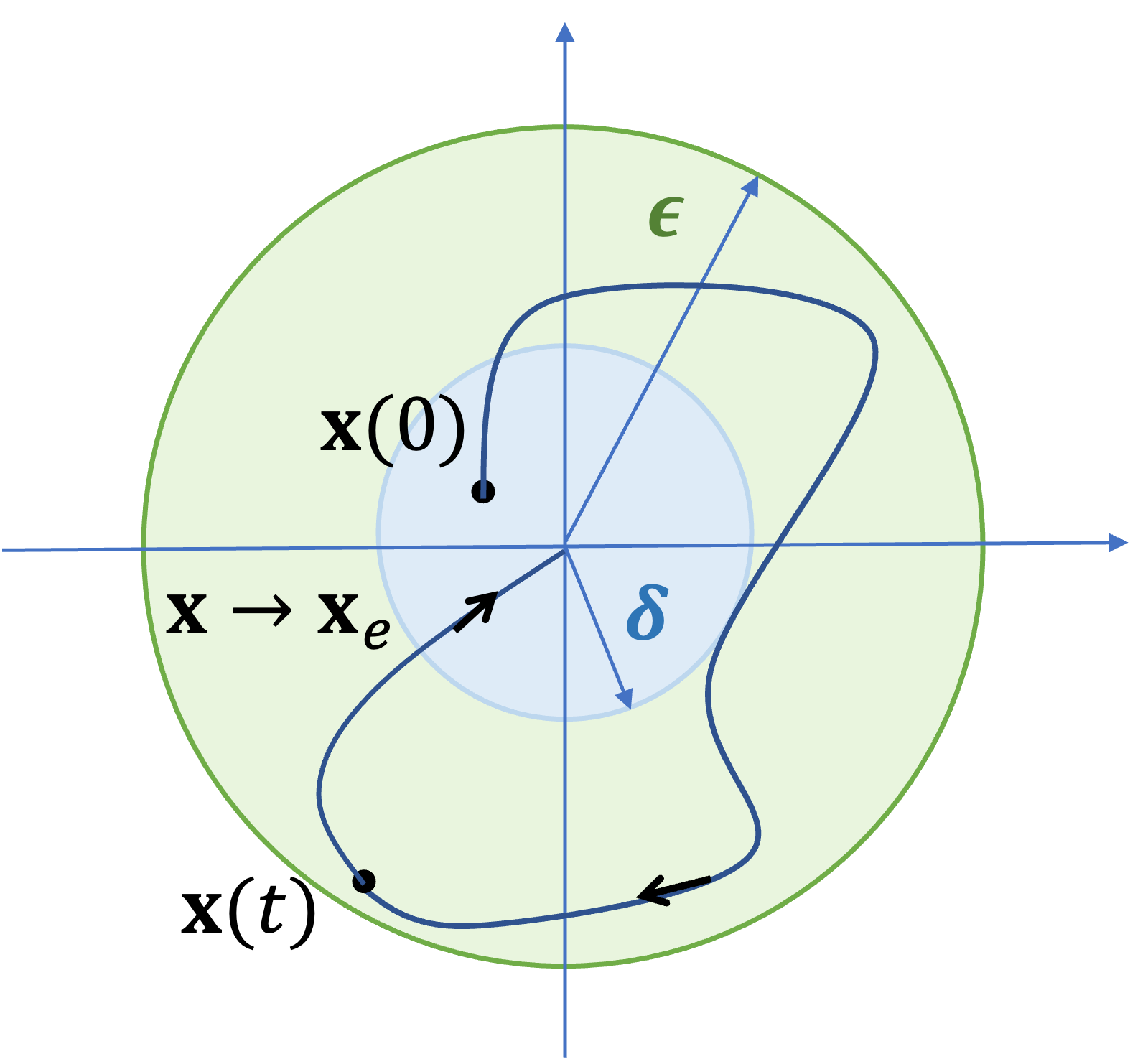
예를 들어서 시스템 (1)에서 평형상태 \(1\) 과 \(-1\) 은 로컬에서 점근적으로 안정하다. 평형상태 \(1\) 의 수렴영역은 \((0, \ \infty)\) 이고 \(-1\) 의 수렴영역은 \( (-\infty, \ 0)\) 이다.
만약 평형상태 \(\mathbf{x}_e\) 가 안정하고 모든 해가 \(\lim_{t \to \infty} \mathbf{x}(t) = \mathbf{x}_e\) 일 경우, 평형상태는 전역(global)에서 점근적(asymptotic)으로 안정하다고 정의한다 (global asymptotic stability).
예를 들어서 다음과 같은 시스템이 있을 때,
\[ \dot{x} = -x \tag{2} \]
이 시스템의 평형상태 \(0\) 은 전역에서 점근적으로 안정하다. 점근적 안정성의 의미는 평형상태가 안정할 뿐만 아니라 시간이 충분히 경과한다면 결국 상태변수가 평형상태로 수렴한다는 뜻이다.
안정성 정의 중에서 가장 강력한 정의는 지수 안정성(exponential stability)이다.
만약 일정 범위 \( \lVert \mathbf{x}(0)-\mathbf{x}_e \rVert \lt \delta\) 에서 시간 \(t \ge 0\) 동안 시스템의 해가 다음 식을 만족하는 \(\beta \gt 0\) 가 존재한다면, 평형상태는 로컬(local)에서 수렴율(rate of convergence) \(\alpha \gt 0\) 인 지수 안정성(exponential stability)을 갖는다고 정의한다.
\[ \lVert \mathbf{x}(t)- \mathbf{x}_e \rVert \le \beta e^{- \alpha t} \lVert \mathbf{x}(0)- \mathbf{x}_e \rVert \mbox{ , for all } \lVert \mathbf{x}(0) - \mathbf{x}_e \rVert \lt \delta \]
지수 안정성은 상태변수 궤적이 어떤 지수 함수보다도 더 빨리 평형상태로 수렴함을 의미한다.
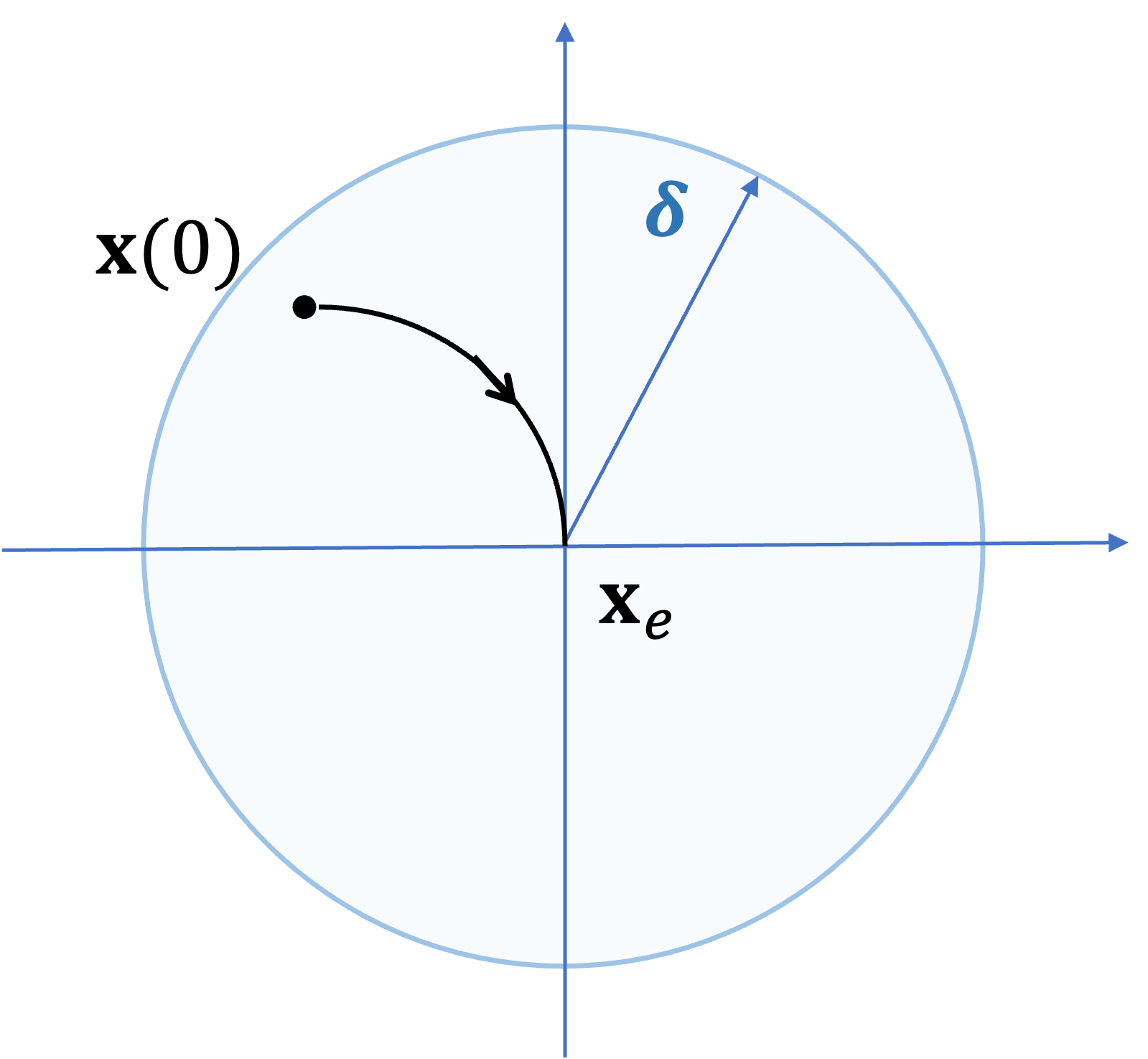
만약 범위가 \(\delta \to \infty\) 라면, 평형상태는 전역(global)에서 지수 안정적이라고 정의한다. 예를 들어서 시스템 (2)에서 평형상태 \(0\) 은 수렴율이 \(\alpha=1\) 인 전역 지수 안정성을 갖는다.
'유도항법제어 > 비행제어' 카테고리의 다른 글
| 행렬지수함수 (Matrix Exponential) 계산 (0) | 2022.12.24 |
|---|---|
| 리야프노프 안정성 (Lyapunov stability) 이론 (0) | 2022.09.30 |
| [Continuous-Time] LTI 시스템과 인과 시스템 (0) | 2022.09.13 |
| [Continuous-Time] LTI 시스템과 컨볼루션 (0) | 2022.09.13 |
| [Continuous-Time] LTI 시스템 (0) | 2022.09.13 |




댓글