MPC는 다음과 같은 제약조건을 갖는 선형 시스템에서
\[ \begin{align} & \mathbf{x}_{t+1}=A \mathbf{x}_t+B \mathbf{u}_t \tag{1} \\ \\ & \mathbf{y}_t=C \mathbf{x}_t \\ \\ & \ \ \ \ \ \mathbf{u}_{min} \le \mathbf{u}_{t+i} \le \mathbf{u}_{max}, \ \ \ i=0, ... , N-1 \tag{2} \\ \\ & \ \ \ \ \ \mathbf{y}_{min} \le \mathbf{y}_{t+i} \le \mathbf{y}_{max}, \ \ \ i=1, ... , N \end{align} \]
매 시간 스텝마다 다음 목적함수가 일정 성능 예측구간 \([t, \ t+N ]\) 에서 최적화되도록 제어입력의 시퀀스 \(\mathbf{u}_{t \ : \ t+N-1}^*=( \mathbf{u}_t^*, \mathbf{u}_{t+1}^*, ... , \mathbf{u}_{t+N-1}^* )\) 를 계산하는 문제다.
\[ \min_{\mathbf{u}_{t \ : \ t+N-1}} J = \mathbf{x}_{t+N}^T Q_f \mathbf{x}_{t+N} + \sum_{i=0}^{N-1} \mathbf{x}_{t+i}^T Q \mathbf{x}_{t+i}+ \mathbf{u}_{t+i}^T R \mathbf{u}_{t+i} \tag{3} \]
실제 제어입력으로는 제어입력의 시퀀스에서 첫 번째 항인 \(\mathbf{u}_t^*\) 만을 사용한다.
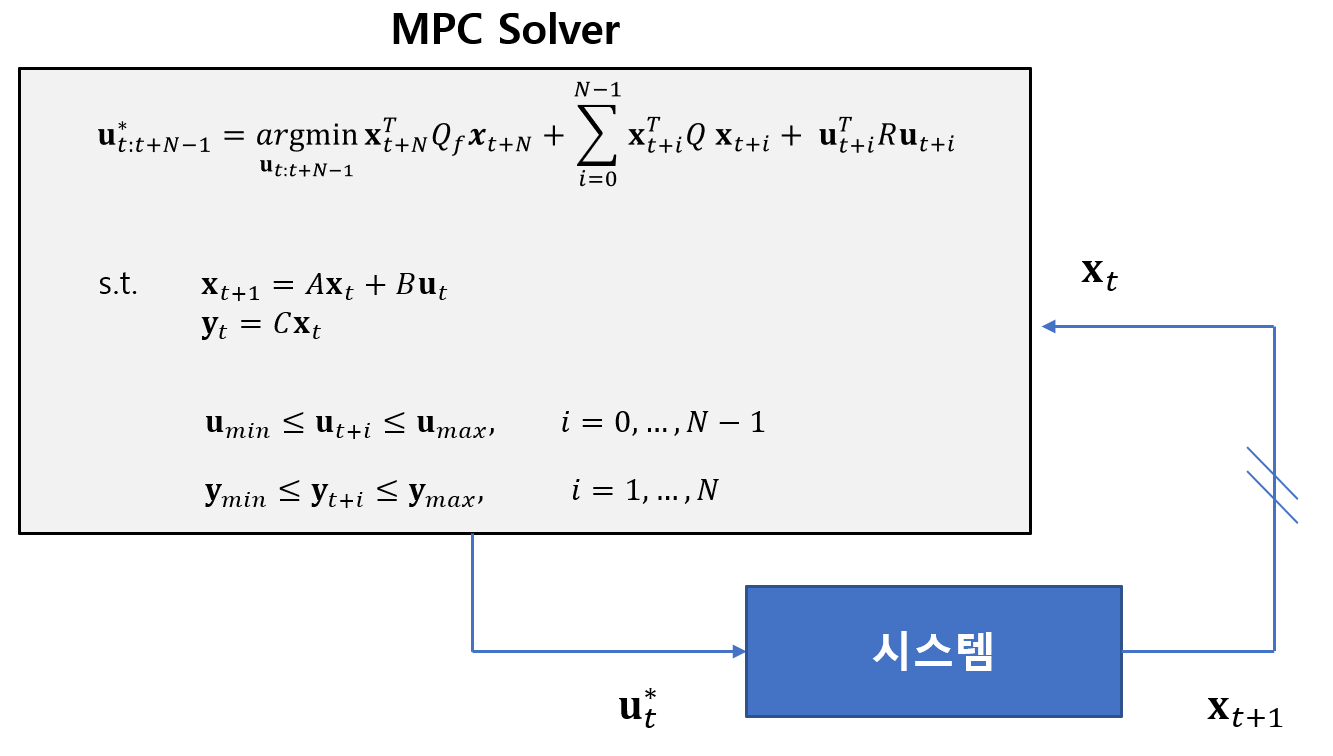
위와 같은 동적 최적화 문제를 QP (quadratic program)문제로 변환한 후 정적 최적화 기법을 적용하여 푸는 것이 일반적인 MPC 알고리즘이다.
여기서는 QP 문제로 변환할 때 사용되는 두가지 방법에 대해서 알아보고자 한다.
먼저 가장 많이 사용되는 범용적 방법에 대해서 설명한다. 식 (1)에 의하면 시간 스텝(time step) \(t\) 부터 \(t+N\) 까지 미래의 상태를 다음과 같이 계산할 수 있다.
\[ \begin{align} & \mathbf{x}_{t+1}=A \mathbf{x}_t+B \mathbf{u}_t \tag{4} \\ \\ & \mathbf{x}_{t+2}=A \mathbf{x}_{t+1}+B \mathbf{u}_{t+1}=A^2 \mathbf{x}_t+AB \mathbf{u}_t+B \mathbf{u}_{t+1} \\ \\ & \ \ \ \ \ \cdots \\ \\ & \mathbf{x}_{t+N}=A^N \mathbf{x}_t+A^{N-1} B \mathbf{u}_t + \cdots + AB \mathbf{u}_{t+N-2}+B \mathbf{u}_{t+N-1} \end{align} \]
식 (4)를 행렬 형식으로 바꾸면 다음과 같이 된다.
\[ \begin{bmatrix} \mathbf{x}_{t+1} \\ \mathbf{x}_{t+2} \\ \mathbf{x}_{t+3} \\ \vdots \\ \mathbf{x}_{t+N} \end{bmatrix} = \begin{bmatrix} A \\ A^2 \\ A^3 \\ \vdots \\ A^N \end{bmatrix} \mathbf{x}_t + \begin{bmatrix} B & 0 & 0 & \cdots & 0 \\ AB & B & 0 & \cdots & 0\\ A^2 B & AB & B & \cdots & 0 \\ \vdots & \vdots & \vdots & ⋱ & \vdots \\ A^{N-1} B & A^{N-2} B & \cdots & AB & B \end{bmatrix} \begin{bmatrix} \mathbf{u}_t \\ \mathbf{u}_{t+1} \\ \mathbf{u}_{t+2} \\ \vdots \\ \mathbf{u}_{t+N-1} \end{bmatrix} \tag{5} \]
또는 다음과 같이 표현할 수 있다.
\[ \mathbf{x}_{t+1 \ ∶ \ t+N }= \Phi \mathbf{x}_t+ \Gamma \mathbf{u}_{t \ ∶ \ t+N-1} \tag{6} \]
여기서
\[ \begin{align} & \mathbf{x}_{t+1 \ ∶ \ t+N } = \begin{bmatrix} \mathbf{x}_{t+1} \\ \mathbf{x}_{t+2} \\ \mathbf{x}_{t+3} \\ \vdots \\ \mathbf{x}_{t+N} \end{bmatrix}, \ \ \ \mathbf{u}_{t \ ∶ \ t+N-1 } = \begin{bmatrix} \mathbf{u}_t \\ \mathbf{u}_{t+1} \\ \mathbf{u}_{t+2} \\ \vdots \\ \mathbf{u}_{t+N-1} \end{bmatrix}, \\ \\ & \Phi = \begin{bmatrix} A \\ A^2 \\ A^3 \\ \vdots \\ A^N \end{bmatrix}, \ \ \ \Gamma = \begin{bmatrix} B & 0 & 0 & \cdots & 0 \\ AB & B & 0 & \cdots & 0\\ A^2 B & AB & B & \cdots & 0 \\ \vdots & \vdots & \vdots & ⋱ & \vdots \\ A^{N-1} B & A^{N-2} B & \cdots & AB & B \end{bmatrix} \end{align} \]
이다. 식 (3)의 목적함수도 다음과 같이 행렬 형식으로 표현할 수 있다.
\[ \begin{align} J &= \mathbf{x}_{t+N}^T Q_f \mathbf{x}_{t+N} + \sum_{i=0}^{N-1} \mathbf{x}_{t+i}^T Q \mathbf{x}_{t+i} + \mathbf{u}_{t+i}^T R \mathbf{u}_{t+i} \tag{7} \\ \\ &= \mathbf{x}_t^T Q \mathbf{x}_t+ \begin{bmatrix} \mathbf{x}_{t+1} & \mathbf{x}_{t+2} & \cdots & \mathbf{x}_{t+N} \end{bmatrix} \begin{bmatrix} Q & & & \\ & Q & & \\ & & ⋱ & \\ & & & Q_f \end{bmatrix}\begin{bmatrix} \mathbf{x}_{t+1} \\ \mathbf{x}_{t+2} \\ \vdots \\ \mathbf{x}_{t+N} \end{bmatrix} \\ \\ & \ \ \ \ \ \ \ \ \ + \begin{bmatrix} \mathbf{u}_t & \mathbf{u}_{t+1} & \cdots & \mathbf{u}_{t+N-1} \end{bmatrix} \begin{bmatrix} R & & & \\ & R & & \\ & & ⋱ & \\ & & & R \end{bmatrix}\begin{bmatrix} \mathbf{u}_t \\ \mathbf{u}_{t+1} \\ \vdots \\ \mathbf{u}_{t+N-1} \end{bmatrix} \\ \\ &= \mathbf{x}_t^T Q \mathbf{x}_t+ \mathbf{x}_{t+1 \ ∶ \ t+N}^T \bar{Q} \mathbf{x}_{t+1 \ ∶ \ t+N} + \mathbf{u}_{t \ ∶ \ t+N-1}^T \bar{R} \mathbf{u}_{t \ ∶ \ t+N-1} \end{align} \]
여기서
\[ \bar{Q}= \begin{bmatrix} Q & & & \\ & Q & & \\ & & ⋱ & \\ & & & Q_f \end{bmatrix}, \ \ \ \bar{R}= \begin{bmatrix} R & & & \\ & R & & \\ & & ⋱ & \\ & & & R \end{bmatrix} \]
이다. 식 (6)을 (7)에 대입하면 식 (7)은 다음과 같이 된다.
\[ \begin{align} J &= \mathbf{x}_t^T Q \mathbf{x}_t+ (\Phi \mathbf{x}_t + \Gamma \mathbf{u}_{t \ ∶ \ t+N-1} )^T \bar{Q} (\Phi \mathbf{x}_t+\Gamma \mathbf{u}_{t \ ∶ \ t+N-1} ) \tag{8} \\ & \ \ \ \ \ \ \ \ \ \ + \mathbf{u}_{t \ ∶ \ t+N-1}^T \bar{R} \mathbf{u}_{t \ ∶ \ t+N-1} \\ \\ &= \mathbf{x}_t^T (Q+\Phi^T \bar{Q} \Phi) \mathbf{x}_t+2 \mathbf{x}_t^T \Phi^T \bar{Q} \Gamma \mathbf{u}_{t \ ∶ \ t+N-1} \\ & \ \ \ \ \ \ \ \ \ \ + \mathbf{u}_{t \ ∶ \ t+N-1}^T (\bar{R} + \Gamma^T \bar{Q} \Gamma) \mathbf{u}_{t \ ∶ \ t+N-1} \\ \\ &= \mathbf{x}_t^T Y \mathbf{x}_t + 2 \mathbf{x}_t^T F^T \mathbf{u}_{t \ ∶ \ t+N-1} + \mathbf{u}_{t \ ∶ \ t+N-1}^T H \mathbf{u}_{t \ ∶ \ t+N-1} \end{align} \]
여기서
\[ Y= Q+\Phi^T \bar{Q} \Phi , \ \ \ F= \Gamma^T \bar{Q} \Phi, \ \ \ H=\bar{R} + \Gamma^T \bar{Q} \Gamma \]
이다. 식 (8)은 \(\mathbf{x}_t\) 의 값이 주어진다는 가정하에 최적화 변수가 \(\mathbf{u}_{t \ ∶ \ t+N-1}\) 인 2차 함수이다.
한편 식 (2)의 제약조건도 \(\mathbf{u}_{t \ ∶ \ t+N-1}\) 의 함수로 표현하기 위해서 수식을 다음과 같이 재 구성한다.
\[ \begin{align} & \begin{bmatrix} I \\ -I \end{bmatrix} \mathbf{u}_{t+i} \le \begin{bmatrix} \mathbf{u}_{max} \\ -\mathbf{u}_{min} \end{bmatrix}, \ \ \ i=0, ... , N-1 \tag{9} \\ \\ & \begin{bmatrix} C \\ -C \end{bmatrix} \mathbf{x}_{t+i} \le \begin{bmatrix} \mathbf{y}_{max} \\ -\mathbf{y}_{min} \end{bmatrix}, \ \ \ i=1, ... , N \end{align} \]
식 (9)를 시간 스텝별로 한 개의 식으로 표현하면 다음과 같이 된다.
\[ \begin{align} & \begin{bmatrix} I \\ -I \end{bmatrix} \mathbf{u}_{t+i} \le \begin{bmatrix} \mathbf{u}_{max} \\ -\mathbf{u}_{min} \end{bmatrix}, \ \ \ i=0 \tag{10} \\ \\ & \begin{bmatrix} 0 \\ 0 \\ C \\ -C \end{bmatrix} \mathbf{x}_{t+i} + \begin{bmatrix} I \\ -I \\ 0 \\ 0 \end{bmatrix} \mathbf{u}_{t+i} \le \begin{bmatrix} \mathbf{u}_{max} \\ -\mathbf{u}_{min} \\ \mathbf{y}_{max} \\ -\mathbf{y}_{min} \end{bmatrix}, \ \ \ i=1, ... , N-1 \\ \\ & \begin{bmatrix} C \\ -C \end{bmatrix} \mathbf{x}_{t+i} \le \begin{bmatrix} \mathbf{y}_{max} \\ -\mathbf{y}_{min} \end{bmatrix}, \ \ \ i=N \end{align} \]
식 (10)에 있는 모든 시간스텝의 제약조건을 한데 묶으면 다음과 같다.
\[ \begin{bmatrix} 0 & \cdots & 0 \\ M_1 & & 0 \\ & ⋱ & \\ 0 & & M_N \end{bmatrix} \begin{bmatrix} \mathbf{x}_{t+1} \\ \vdots \\ \mathbf{x}_{t+N} \end{bmatrix} + \begin{bmatrix} E_0 & & 0 \\ & ⋱ & \\ 0 & & E_{N-1} \\ 0 & \cdots & 0 \end{bmatrix} \begin{bmatrix} \mathbf{u}_t \\ \vdots \\ \mathbf{u}_{t+N-1} \end{bmatrix} \le \begin{bmatrix} \mathbf{b}_0 \\ \mathbf{b}_1 \\ \vdots \\ \mathbf{b}_N \end{bmatrix} \tag{11} \]
또는
\[ \bar{M} \mathbf{x}_{t+1 \ ∶ \ t+N } + \bar{E} \mathbf{u}_{t \ ∶ \ t+N-1} \le \bar{\mathbf{b}} \tag{12} \]
이다. 여기서
\[ \begin{align} & M_i = \begin{bmatrix} 0 \\ 0 \\ C \\ -C \end{bmatrix}, \ \ \ E_i = \begin{bmatrix} I \\ -I \\ 0 \\ 0 \end{bmatrix}, \ \ \ \mathbf{b}_i= \begin{bmatrix} \mathbf{u}_{max} \\ -\mathbf{u}_{min} \\ \mathbf{y}_{max} \\ -\mathbf{y}_{min} \end{bmatrix}, \ \ \ i=1, ... , N-1 \\ \\ & E_0 = \begin{bmatrix} I \\ -I \end{bmatrix}, \ \ \ \mathbf{b}_0 = \begin{bmatrix} \mathbf{u}_{max} \\ -\mathbf{u}_{min} \end{bmatrix}, \ \ \ M_N= \begin{bmatrix} C \\ -C \end{bmatrix}, \ \ \ \mathbf{b}_N=\begin{bmatrix} \mathbf{y}_{max} \\ -\mathbf{y}_{min} \end{bmatrix} , \\ \\ & \bar{M}=\begin{bmatrix} 0 & \cdots & 0 \\ M_1 & & 0 \\ & ⋱ & \\ 0 & & M_N \end{bmatrix}, \ \ \ \bar{E} = \begin{bmatrix} E_0 & & 0 \\ & ⋱ & \\ 0 & & E_{N-1} \\ 0 & \cdots & 0 \end{bmatrix}, \ \ \ \bar{\mathbf{b}} = \begin{bmatrix} \mathbf{b}_0 \\ \mathbf{b}_1 \\ \vdots \\ \mathbf{b}_N \end{bmatrix} \end{align} \]
이다. 식 (6)을 (12)에 대입하면 다음과 같이 된다.
\[ \bar{M} (\Phi \mathbf{x}_t+ \Gamma \mathbf{u}_{t \ ∶ \ t+N-1} ) + \bar{E} \mathbf{u}_{t \ ∶ \ t+N-1} \le \bar{\mathbf{b}} \tag{13} \]
위 식은 다음과 같이 쓸 수 있다.
\[ (\bar{M} \Gamma + \bar{E} ) \mathbf{u}_{t \ ∶ \ t+N-1} \le \bar{\mathbf{b}} - \bar{M} \Phi \mathbf{x}_t \tag{14} \]
정리하면 식 (1), (2), (3)으로 주어지는 MPC의 동적 최적화 문제는 다음과 같이 QP 최적화 문제로 변환된다.
\[ \begin{align} & \min_{\mathbf{u}_{t \ : \ t+N-1}} J = \mathbf{x}_t^T Y \mathbf{x}_t+2 \mathbf{x}_t^T F^T \mathbf{u}_{t \ ∶ \ t+N-1} + \mathbf{u}_{t \ ∶ \ t+N-1}^T H \mathbf{u}_{t \ ∶ \ t+N-1} \tag{15} \\ \\ & \mbox{subject to } \ \ (\bar{M} \Gamma + \bar{E} ) \mathbf{u}_{t \ ∶ \ t+N-1} \le \bar{\mathbf{b}} -\bar{M} \Phi \mathbf{x}_t \end{align} \]
여기서 \(\mathbf{x}_t\) 는 측정할 수 있다고 가정한다. 위 식에서 목적함수의 첫번째 항은 최적화 변수의 함수가 아니므로 최종적으로 다음과 같은 QP 문제를 유도할 수 있다.
\[ \begin{align} & \min_{\mathbf{u}_{t \ : \ t+N-1}} \tilde{J} = 2 \mathbf{x}_t^T F^T \mathbf{u}_{t \ ∶ \ t+N-1} + \mathbf{u}_{t \ ∶ \ t+N-1}^T H \mathbf{u}_{t \ ∶ \ t+N-1} \tag{16} \\ \\ & \mbox{subject to } \ \ (\bar{M} \Gamma + \bar{E} ) \mathbf{u}_{t \ ∶ \ t+N-1} \le \bar{\mathbf{b}} -\bar{M} \Phi \mathbf{x}_t \end{align} \]
QP 솔버는 여러가지가 있지만 만약 Matlab을 사용하여 풀려면 함수 'quadprog' 를 사용하면 된다.

범용 솔버를 사용하여 QP문제를 풀 경우 시간이 많이 소요되기 때문에 MPC는 전통적으로 샘플 시간이 초 또는 분 단위로 측정되는 느린 역학을 가진 시스템으로 적용이 제한되었다. 반응 속도가 빠른 시스템에 MPC를 구현하는 한 가지 방안으로 모든 상태변수에 대해서 제어값을 미리 오프라인해서 계산한 다음 제어값을 룩업 테이블(lookup table)의 형태로 온라인으로 구현하는 방법이 있다. 이것이 explicit MPC 또는 리얼타임 MPC의 아이디어이다.
이 방법의 단점은 테이블의 항목 수가 예측구간, 상태 및 입력변수의 차원에 따라 기하급수적으로 증가할 수 있어서 테이블을 조회하는 시간 역시 기하급수적으로 증가한다는 데 있다. 하지만 룩업 테이블 대신에 최근 발전하고 있는 인공 신경망 기술을 이용하여 테이블을 피팅한다면 고속으로 제어입력을 계산해 낼 수 있을 것으로 생각된다.
'유도항법제어 > 최적제어' 카테고리의 다른 글
| [Continuous-Time] 최적제어 문제 (0) | 2022.12.13 |
|---|---|
| [MPC] MPC를 위한 두가지 QP 모델 - 2 (0) | 2022.12.03 |
| [MPC] 모델예측제어 개요 (0) | 2022.11.28 |
| [PSOC-7] 유사 스펙트럴 방법 예제 (0) | 2022.04.24 |
| [PSOC-6] 유사 스펙트럴 방법 (Pseudospectral Method) (0) | 2022.04.23 |




댓글