베이즈 필터(Bayes filter)는 이산시간(discrete-time) 확률 동적 시스템(stochastic dynamical system)의 상태변수를 추정하기 위한 확률론적인 방법으로서 칼만필터를 비롯한 대부분의 상태변수 추정 알고리즘의 근간을 이룬다.
베이즈 필터 문제는 초기 시간 \(0\) 부터 시간스텝 \(t\) 까지의 측정값 시퀀스
\[ \mathbf{z}_{0:t} = \{\mathbf{z}_0, \mathbf{z}_1, ... , \mathbf{z}_t \} \tag{1} \]
와 초기 시간 \(0\) 부터 시간스텝 \(t\) 까지의 제어입력(또는 행동)의 시퀀스
\[ \mathbf{u}_{0:t} = \{\mathbf{u}_0, \mathbf{u}_1, ... , \mathbf{u}_t \} \tag{2} \]
가 주어졌을 때, 이를 조건으로 하여 상태변수의 시퀀스 \(\{ \mathbf{x}_1, \mathbf{x}_2, ... , \mathbf{x}_t \}\) 를 추정하는 것이다.
상태변수 \(\mathbf{x}_t\) 에 관한 모든 정보는 확률밀도함수를 통해 파악할 수 있으므로, 베이즈 필터 문제는 측정값의 시퀀스 \(\mathbf{z}_{0:t}\) 와 제어입력의 시퀀스 \(\mathbf{u}_{0:t}\) 를 조건으로 한 상태변수 \(\mathbf{x}_t\) 의 조건부 확률밀도함수
\[ p( \mathbf{x}_t | \mathbf{z}_{0:t}, \mathbf{u}_{0:t} ) \tag{3} \]
를 구하는 문제로 귀결된다.
베이즈 필터에서 사용하는 가정은,
첫째, 시스템 모델은 마르코프(Markov) 시퀀스이고,
둘째, 측정값 \(\mathbf{z}_t\) 는 상태변수 \(\mathbf{x}_t\) 에만 의존한다.
라는 것이다. 수식으로 표현하면 다음과 같다.
\[ \begin{align} & p(\mathbf{x}_t | \mathbf{x}_{0:t-1}, \mathbf{z}_{0:t}, \mathbf{u}_{0:t}) = p(\mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{u}_{t-1}) \tag{4} \\ \\ & p(\mathbf{z}_t | \mathbf{x}_{0:t}, \mathbf{z}_{0:t}, \mathbf{u}_{0:t}) = p(\mathbf{z}_t | \mathbf{x}_t) \tag{5} \end{align} \]
식 (4)를 시스템 (또는 환경) 모델이라고 하고 식 (5)를 비메모리(memoryless) 측정 모델(또는 센서 모델)이라고 한다. 식 (4)의 가정에 의하면 상태변수 \(\mathbf{x}_t\) 는 제어입력 \(\mathbf{u}_t\) 의 영향을 받지 않으므로 식 (2)와 식 (3)의 제어입력 시퀀스는 \(\mathbf{u}_{0:t}\) 대신에 초기 시간 \(0\) 부터 시간스텝 \(t-1\) 까지의 제어입력 시퀀스 \(\mathbf{u}_{0:t-1}\) 을 사용한다.
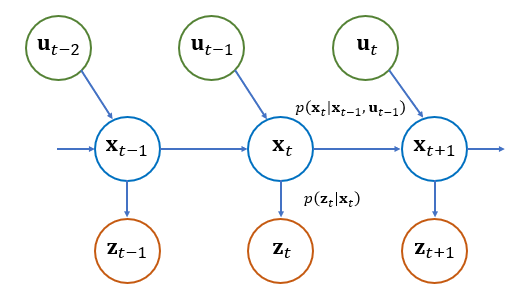
이제 상태변수 \(\mathbf{x}_t\) 의 조건부 확률밀도함수를 구하기 위해서 베이즈 정리를 이용하여 식 (3)을 전개해보자.
\[ \begin{align} p(\mathbf{x}_t |\mathbf{z}_{0:t}, \mathbf{u}_{0:t-1}) &= \frac{ p(\mathbf{z}_{0:t} | \mathbf{x}_t, \mathbf{u}_{0:t-1}) p(\mathbf{x}_t | \mathbf{u}_{0:t-1} ) }{ p(\mathbf{z}_{0:t} | \mathbf{u}_{0:t-1}) } \tag{6} \\ \\ &= \frac{ p( \mathbf{z}_t, \mathbf{z}_{0:t-1} | \mathbf{x}_t, \mathbf{u}_{0:t-1}) p(\mathbf{x}_t | \mathbf{u}_{0:t-1} ) }{ p( \mathbf{z}_t, \mathbf{z}_{0:t-1} | \mathbf{u}_{0:t-1}) } \\ \\ &= \frac{ p( \mathbf{z}_t | \mathbf{z}_{0:t-1}, \mathbf{x}_t, \mathbf{u}_{0:t-1}) p(\mathbf{z}_{0:t-1} | \mathbf{x}_t, \mathbf{u}_{0:t-1}) p(\mathbf{x}_t | \mathbf{u}_{0:t-1} ) }{ p( \mathbf{z}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) p(\mathbf{z}_{0:t-1} | \mathbf{u}_{0:t-1}) } \end{align} \]
여기서 다음과 같은 관계식을 이용하면,
\[ p(\mathbf{z}_{0:t} | \mathbf{x}_t, \mathbf{u}_{0:t-1}) = \frac{ p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) p(\mathbf{z}_{0:t-1} | \mathbf{u}_{0:t-1}) }{ p(\mathbf{x}_t | \mathbf{u}_{0:t-1} ) } \tag{7} \]
식 (6)은 다음과 같이 된다.
\[ p(\mathbf{x}_t |\mathbf{z}_{0:t}, \mathbf{u}_{0:t-1}) = \frac{ p( \mathbf{z}_t | \mathbf{z}_{0:t-1}, \mathbf{x}_t, \mathbf{u}_{0:t-1}) p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1} ) }{ p( \mathbf{z}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) } \tag{8} \]
식 (5)에 의하면, 식 (8)은 다음과 같이 된다.
\[ p(\mathbf{x}_t | \mathbf{z}_{0:t}, \mathbf{u}_{0:t-1}) = \frac{ p( \mathbf{z}_t | \mathbf{x}_t) p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1} ) }{ p( \mathbf{z}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) } \tag{9} \]
여기서 \( p(\mathbf{x}_t |\mathbf{z}_{0:t}, \mathbf{u}_{0:t-1}) \) 는 \(\mathbf{z}_t\) 값을 측정을 한 후의 확률밀도함수이기 때문에 사후(a posteriori) 확률밀도함수라고 하고, \( p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1} ) \) 는 \(\mathbf{z}_t\) 값을 측정하기 전의 확률밀도함수이기 때문에 사전(a priori) 확률밀도함수라고 한다. \( p( \mathbf{z}_t | \mathbf{x}_t) \) 는 빈도함수(likelihood function)라고 하고, \( p( \mathbf{z}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) \) 를 정규화(normalizing) 항이라고 하는데 다음과 같이 계산할 수 있다.
\[ p( \mathbf{z}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) = \int_{\mathbf{x}_t} p( \mathbf{z}_t | \mathbf{x}_t) p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) \ d\mathbf{x}_t \tag{10} \]
식 (10)을 식 (9)에 대입하면 다음 식을 얻을 수 있다.
\[ p(\mathbf{x}_t | \mathbf{z}_{0:t}, \mathbf{u}_{0:t-1}) = \frac{ p( \mathbf{z}_t | \mathbf{x}_t) p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1} ) }{ \int_{\mathbf{x}_t} p( \mathbf{z}_t | \mathbf{x}_t) p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) \ d\mathbf{x}_t } \tag{11} \]
식 (11)은 \( p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1} ) \) 이 주어졌을 때, 측정 모델 \( p( \mathbf{z}_t | \mathbf{x}_t) \) 를 이용하여 \( p(\mathbf{x}_t | \mathbf{z}_{0:t}, \mathbf{u}_{0:t-1}) \) 을 계산할 수 있는 식이기 때문에 측정 업데이트(measurement update)식이라고 한다.
식 (11)의 사전 확률밀도함수를 좀 더 전개하면 다음과 같다.
\[ \begin{align} p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) &= \int_{\mathbf{x}_{t-1}} p( \mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1} ) p( \mathbf{x}_{t-1} | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) \ d\mathbf{x}_{t-1} \tag{12} \\ \\ &= \int_{\mathbf{x}_{t-1}} p( \mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{u}_{t-1} ) p( \mathbf{x}_{t-1} | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-2}) \ d\mathbf{x}_{t-1} \end{align} \]
여기서 \(\mathbf{x}_t\) 가 마르코프 시퀀스라는 가정인 식 (4)를 사용하였다. 위 식의 두 번째 줄에서 \(\mathbf{u}_{0:t-1}\) 이 \(\mathbf{u}_{0:t-2}\) 로 바뀐 이유는 제어입력 \(\mathbf{u}_{t-1}\) 이 상태변수 \(\mathbf{x}_{t-1}\) 에 영향을 미치지 않기 때문에 제거한 것이다. 위 식은 \( p( \mathbf{x}_{t-1} | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-2}) \) 가 주어졌을 때, 시스템 모델 \( p( \mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{u}_{t-1} ) \) 을 이용하여 \( p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) \) 을 계산할 수 있는 식이기 때문에 시간 업데이트(time update)식 또는 상태 예측(state prediction)식이라고 한다.
정리하면 베이즈 필터는 시간 업데이트식과 측정 업데이트식 등 2개의 식이 번갈아 작동하는 궤환 필터(recursive filter)이다.
\[ \begin{align} & p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) = \int_{\mathbf{x}_{t-1}} p( \mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{u}_{t-1} ) p( \mathbf{x}_{t-1} | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-2}) \ d\mathbf{x}_{t-1} \tag{13} \\ \\ & p(\mathbf{x}_t | \mathbf{z}_{0:t}, \mathbf{u}_{0:t-1}) = \frac{ p( \mathbf{z}_t | \mathbf{x}_t) p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1} ) }{ \int_{\mathbf{x}_t} p( \mathbf{z}_t | \mathbf{x}_t) p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) \ d\mathbf{x}_t } \end{align} \]
식 (13)을 한 개의 식으로 합칠 수도 있다.
\[ \begin{align} p(\mathbf{x}_t | \mathbf{z}_{0:t}, \mathbf{u}_{0:t-1}) &= \frac{ p( \mathbf{z}_t | \mathbf{x}_t) \int_{\mathbf{x}_{t-1}} p( \mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{u}_{t-1} ) p( \mathbf{x}_{t-1} | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-2}) \ d\mathbf{x}_{t-1} }{ \int_{\mathbf{x}_t} p( \mathbf{z}_t | \mathbf{x}_t) p(\mathbf{x}_t | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-1}) \ d\mathbf{x}_t } \tag{14} \\ \\ &= \eta \ p( \mathbf{z}_t | \mathbf{x}_t) \int_{\mathbf{x}_{t-1}} p( \mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{u}_{t-1} ) p( \mathbf{x}_{t-1} | \mathbf{z}_{0:t-1}, \mathbf{u}_{0:t-2}) \ d\mathbf{x}_{t-1} \end{align} \]
여기서 \(\eta\) 는 식 (10)으로 주어지는 정규화 항이다.
로봇이나 SLAM 커뮤니티에서는 사후 확률밀도함수인 \( p(\mathbf{x}_t | \mathbf{z}_{0:t}, \mathbf{u}_{0:t-1}) \) 을 \(bel(\mathbf{x}_t)\) 라고 표기하고 시간스텝 \(t\) 에서의 belief state라고 한다. 이 표기에 의하면 베이즈 필터 식 (14)를 다음과 같이 쓸 수 있다.
\[ bel(\mathbf{x}_t) = \eta \ p( \mathbf{z}_t | \mathbf{x}_t) \int_{\mathbf{x}_{t-1}} p( \mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{u}_{t-1} ) \ bel( \mathbf{x}_{t-1} ) \ d\mathbf{x}_{t-1} \tag{15} \]
베이즈 필터는 시간스텝 \(t-1\) 에서 주어진 사후 확률밀도함수로부터 시간스텝 \(t\) 에서의 사후 확률밀도함수를 계산할 수 있는 개념적인 필터로서, 극히 제한적인 조건 하에서만 해석적인 해를 얻을 수 있다. 칼만필터와 그리드(grid) 기반 필터가 그 예다.

'유도항법제어 > 칼만필터를 넘어서' 카테고리의 다른 글
| 이노베이션 (Innovation)의 확률적 특성 (0) | 2024.12.15 |
|---|---|
| [PF-2] SIS에서 파티클 필터로 (0) | 2021.07.11 |
| [PF-1] 순차 중요 샘플링 (Sequential Importance Sampling) (0) | 2021.06.13 |
| 칼만필터 알고리즘 (0) | 2021.03.04 |
| 칼만필터란 무엇인가 (0) | 2021.03.03 |




댓글