칼만필터는 수학 알고리즘이다. 따라서 수학식 없이는 칼만필터를 사용할 수도 이해할 수도 없다. 그렇다고 칼만필터 유도과정을 자세히 이해할 필요까지는 없다. 결과만 잘 이해하고 있어도 칼만필터를 사용할 수 있다.
우선 칼만필터 알고리즘을 수학식으로 써 보겠다. 칼만필터는 다음과 같이 주어진 선형 동적 시스템 모델과 측정 모델,
\[ \begin{align} & \mathbf{x}_{t+1}= F_t \mathbf{x}_t+G_t \mathbf{u}_t+ \mathbf{w}_t \\ \\ & \mathbf{z}_t=H_t \mathbf{x}_t+ \mathbf{v}_t \end{align} \]
을 이용하여, 시스템의 상태변수 \(\mathbf{x}(k)\)를 다음과 같이 시간 업데이트와 측정 업데이트 등 두 단계로 추정하는 알고리즘이다.
칼만필터 알고리즘
시간 업데이트:
\[ \begin{align} & \hat{\mathbf{x}}_{t+1|t}= F_t \hat{\mathbf{x}}_{t|t}+G_t \mathbf{u}_t \\ \\ & P_{t+1|t}=F_tP_{t|t} F^T_t+Q_t \end{align} \]
측정 업데이트:
\[ \begin{align} & \hat{\mathbf{x}}_{t|t}= \hat{\mathbf{x}}_{t|t-1}+ K_t \left( \mathbf{z}_t - H_t \hat{\mathbf{x}}_{t|t-1} \right) \\ \\ & K_t=P_{t|t-1} H^T_t S^{-1}_t \\ \\ & S_t=H_tP_{t|t-1} H^T_t+R_t \\ \\ & P_{t|t}=P_{t|t-1}- P_{t|t-1} H^T_t S^{-1}_t H_tP_{t|t-1} \end{align} \]
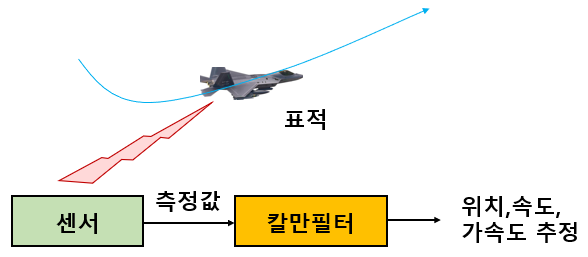
칼만필터 알고리즘은 위에 있는 6줄의 수학식이 전부다. 저 6줄의 수학식을 파이썬, 매트랩, C, C++, C# 등 컴퓨터 언어로 코딩하면 된다. 정말 저 6줄이 다인가? 그렇다. 그래서 칼만필터 알고리즘은 간단하다고 했다. 물론 이해하고 응용하는 것은 별 문제다. 칼만필터를 비선형 시스템에 적용하거나 센서 융합, 고장 진단, 적 항공기 추적, 로컬라이제이션 문제에 응용하기 위해서는 칼만필터의 수식을 잘 이해해야 한다.
칼만필터 알고리즘의 수식을 이해하기에 앞서 우선 수식에 쓰인 \(\mathbf{x}, \mathbf{z}, \mathbf{w}, \mathbf{v}, F, G, H, P, Q, R, t\) 등등 기호가 의미하는 바가 뭔지 알아야 한다. 또한 칼만필터 알고리즘을 유도할 때 사용된 가정(assumption)도 정확히 이해해야 한다. 칼만필터의 유도과정은 몰라도 된다. 하지만 칼만필터를 이해하는 데에도 관련 수학지식이 많이 필요하다.
'유도항법제어 > 칼만필터를 넘어서' 카테고리의 다른 글
| 이노베이션 (Innovation)의 확률적 특성 (0) | 2024.12.15 |
|---|---|
| [PF-2] SIS에서 파티클 필터로 (0) | 2021.07.11 |
| [PF-1] 순차 중요 샘플링 (Sequential Importance Sampling) (0) | 2021.06.13 |
| 베이즈 필터 (Bayes Filter) (0) | 2021.06.08 |
| 칼만필터란 무엇인가 (0) | 2021.03.03 |




댓글