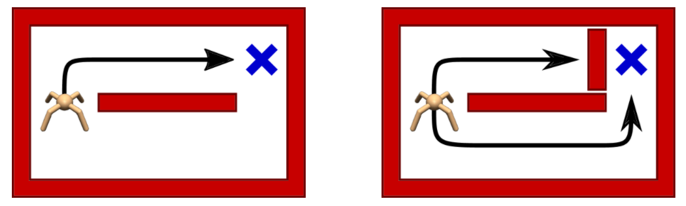
강화학습 에이전트가 최적 경로를 선택하는 것만을 학습한다면 환경 변화에 매우 취약할 것이다.
환경 변화는 실제 세계에서 늘 벌어지는 일이므로 학습시에 최적의 선택과 함께 차선의 선택도 학습한다면 에이전트가 환경 변화에 보다 강인하게 대처할 수 있을 것이다.
강화학습의 목표는 다음과 같이 반환값(누적 보상)의 기댓값으로 이루어진 목적함수를 최대로 만드는 것이었다.
\[ J= \mathbb{E}_{\tau \sim p(\tau) } \left[ \sum_{t=0}^T \gamma^t r(\mathbf{x}_t, \mathbf{u}_t ) \right] \]
그런데 이와 같은 표준 목적함수를 확장시켜서 '정책의 로그함수'를 추가한 새로운 목적함수를 생각해 보자.
\[ J= \mathbb{E}_{\tau \sim p(\tau) } \left[ \sum_{t=0}^T \gamma^t \left( r(\mathbf{x}_t, \mathbf{u}_t ) -\alpha \log \pi (\mathbf{u}_t | \mathbf{u}_t ) \right) \right] \]
위 목적함수는 다음과 같은 형식으로도 쓸 수 있다.
\[ \begin{align} J &= \int_\tau \left[ \sum_{t=0}^T \gamma^t \left( r(\mathbf{x}_t, \mathbf{u}_t ) -\alpha \log \pi (\mathbf{u}_t | \mathbf{u}_t ) \right) \right] p(\tau) d\tau \\ \\ &= \sum_{t=0}^T \int_{(\mathbf{x}_t, \mathbf{u}_t )} \left[ \gamma^t \left( r(\mathbf{x}_t, \mathbf{u}_t ) - \alpha \log \pi (\mathbf{u}_t | \mathbf{x}_t ) \right) \right] p(\mathbf{x}_t, \mathbf{u}_t ) d\mathbf{x}_t d\mathbf{u}_t \\ \\ &= \sum_{t=0}^T \mathbb{E}_{(\mathbf{x}_t, \mathbf{u}_t) \sim p(\mathbf{x}_t, \mathbf{u}_t ) } \left[ \gamma^t \left( r(\mathbf{x}_t, \mathbf{u}_t ) - \alpha \log \pi (\mathbf{u}_t | \mathbf{x}_t ) \right) \right] \end{align} \]
위 식을 전개해 보면,
\[ \begin{align} J &= \sum_{t=0}^T \mathbb{E}_{(\mathbf{x}_t, \mathbf{u}_t) \sim p(\mathbf{x}_t, \mathbf{u}_t ) } \left[ \gamma^t r(\mathbf{x}_t, \mathbf{u}_t ) \right] - \sum_{t=0}^T \alpha \gamma^t \mathbb{E}_{(\mathbf{x}_t, \mathbf{u}_t) \sim p(\mathbf{x}_t, \mathbf{u}_t ) } \left[ \log \pi (\mathbf{u}_t | \mathbf{x}_t ) \right] \\ \\ &= \sum_{t=0}^T \mathbb{E}_{(\mathbf{x}_t, \mathbf{u}_t) \sim p(\mathbf{x}_t, \mathbf{u}_t ) } \left[ \gamma^t r(\mathbf{x}_t, \mathbf{u}_t ) \right] - \sum_{t=0}^T \alpha \gamma^t \int_{(\mathbf{x}_t, \mathbf{u}_t) } \log \pi (\mathbf{u}_t | \mathbf{x}_t ) p(\mathbf{x}_t, \mathbf{u}_t ) d\mathbf{x}_t d\mathbf{u}_t \\ \\ &= \sum_{t=0}^T \mathbb{E}_{(\mathbf{x}_t, \mathbf{u}_t) \sim p(\mathbf{x}_t, \mathbf{u}_t ) } \left[ \gamma^t r(\mathbf{x}_t, \mathbf{u}_t ) \right] - \sum_{t=0}^T \alpha \gamma^t \int_{(\mathbf{x}_t, \mathbf{u}_t) } \log \pi (\mathbf{u}_t | \mathbf{x}_t ) \pi(\mathbf{u}_t | \mathbf{x}_t ) p(\mathbf{x}_t) d\mathbf{x}_t d\mathbf{u}_t \\ \\ &= \sum_{t=0}^T \mathbb{E}_{(\mathbf{x}_t, \mathbf{u}_t) \sim p(\mathbf{x}_t, \mathbf{u}_t ) } \left[ \gamma^t r(\mathbf{x}_t, \mathbf{u}_t ) \right] + \sum_{t=0}^T \alpha \gamma^t \int_{\mathbf{x}_t} \mathcal{H} (\pi (\mathbf{u}_t | \mathbf{x}_t ) ) p(\mathbf{x}_t) d\mathbf{x}_t \\ \\ &= \sum_{t=0}^T \mathbb{E}_{(\mathbf{x}_t, \mathbf{u}_t) \sim p(\mathbf{x}_t, \mathbf{u}_t ) } \left[ \gamma^t r(\mathbf{x}_t, \mathbf{u}_t ) \right] + \sum_{t=0}^T \gamma^t \mathbb{E}_{\mathbf{x}_t \sim p(\mathbf{x}_t)} \left[ \alpha \mathcal{H} (\pi (\mathbf{u}_t | \mathbf{x}_t ) ) \right] \end{align} \]
가 된다. 여기서 \(\mathcal{H} (\pi (\mathbf{u}_t | \mathbf{x}_t ))\) 는 정책 \(\pi (\mathbf{u}_t | \mathbf{x}_t )\) 의 엔트로피(entropy)로서 다음과 같이 정의된다.
\[ \mathcal{H} (\pi (\mathbf{u}_t | \mathbf{x}_t )) = -\int_{\mathbf{u}_t } \log \pi (\mathbf{u}_t | \mathbf{x}_t ) \pi(\mathbf{u}_t | \mathbf{x}_t ) d\mathbf{u}_t \]
위 목적함수는 기존의 목적함수에 정책의 엔트로피를 추가한 것으로서 이 새로운 목적함수를 최대 엔트로피(maximum entropy) 목적함수라고 한다.
\[ J = \sum_{t=0}^T \mathbb{E}_{(\mathbf{x}_t, \mathbf{u}_t) \sim p(\mathbf{x}_t, \mathbf{u}_t ) } \left[ \gamma^t r(\mathbf{x}_t, \mathbf{u}_t ) \right] + \sum_{t=0}^T \gamma^t \mathbb{E}_{\mathbf{x}_t \sim p(\mathbf{x}_t)} \left[ \alpha \mathcal{H} (\pi (\mathbf{u}_t | \mathbf{x}_t ) ) \right] \]
여기서 \(\alpha\) 는 온도 파라미터(temperature parameter)라고 하며 엔트로피와 반환값의 상대적인 중요성을 결정한다. 온도가 높을수록 분자의 움직임이 빨라지며 무작위성이 커지는 것에서 그 이름을 차용한 것으로 짐작된다.
최대 엔트로피 목적함수에 의하면 기존의 반환값뿐만 아니라 정책의 엔트로피도 동시에 최대화시킨다는 의도가 있다. 정책 엔트로피는 확률분포가 균일할 때 최대값을 가지므로 목적함수에 이를 더함으로써 에이전트가 최대한 무작위적으로 움직이게 하려는 목적이 있다.
\(\alpha\) 가 크면 정책의 무작위성이 커지고, 반대로 \(\alpha\) 가 작다면 정책의 확정적 경향성이 더 커진다. 정책의 무작위성이 커진다는 의미는 최적뿐만 아니라 준최적인 행동도 선택될 수 있다는 뜻이다.
최대 엔트로피 목적함수 식은 다음과 같이 다음과 같이 엔트로피를 확률밀도함수 \(p(\mathbf{x}_t, \mathbf{u}_t )\) 기반의 기댓값 연산자 안으로 넣어서 간략하게 표현하기도 한다. 대신 엔트로피 연산자의 \(\mathbf{u}_t\) 항을 점(dot)으로 표현한다.
\[ J = \sum_{t=0}^T \gamma^t \ \mathbb{E}_{(\mathbf{x}_t, \mathbf{u}_t) \sim p(\mathbf{x}_t, \mathbf{u}_t ) } \left[ r(\mathbf{x}_t, \mathbf{u}_t ) + \alpha \mathcal{H} (\pi (\cdot | \mathbf{x}_t ) ) \right] \]
최대 엔트로피 목적함수 하에서는 표준 상태가치 함수도 엔트로피를 포함하도록 수정돼야 한다.
표준 상태가치 함수의 정의는 어떤 상태변수 \(\mathbf{x}_t\) 에서 시작하여 그로부터 어떤 정책 \(\pi\) 에 의해서 행동이 가해졌을 때 기대할 수 있는 미래 보상의 총합이었다.
\[ V^\pi (\mathbf{x}_t )= \mathbb{E}_{\tau_{u_t : u_T } \sim p(\tau_{u_t:u_T } | \mathbf{x}_t )} \left[ \sum_{k=t}^T \gamma^{k-t} r(\mathbf{x}_k, \mathbf{u}_k ) \right] \]
여기서 \(\tau_{u_t:u_T} = (\mathbf{u}_t, \mathbf{x}_{t+1}, \mathbf{u}_{t+1}, ... , \mathbf{u}_T)\) 는 상태변수 \(\mathbf{x}_t\) 에서 시작하여 그로부터 어떤 정책 \(\pi\) 로 생성되는 궤적이다. 위 정의에서 기댓값 연산자 안의 수식은 목적함수이다.
표준 상태가치 함수에서 최대 엔트로피 목적함수를 고려한다면 새로운 상태가치 함수를 다음과 같이 정의할 수 있다.
\[ V^\pi_{soft} (\mathbf{x}_t )= \mathbb{E}_{\tau_{u_t : u_T } \sim p(\tau_{u_t:u_T } | \mathbf{x}_t )} \left[ \sum_{k=t}^T \gamma^{k-t} \left( r(\mathbf{x}_k, \mathbf{u}_k ) -\alpha \log \pi (\mathbf{u}_k | \mathbf{x}_k ) \right) \right] \]
마찬가지로 기댓값 연산자 안의 수식은 최대 엔트로피 목적함수이다. 위 식은 상태가치 함수에 엔트로피를 추가한 것으로서 소프트 상태가치 함수(soft state-value function)라고 한다. 그러면 최대 엔트로피 목적함수와 소프트 상태가치 함수는 다음과 같은 관계식을 갖는다.
\[ J=\mathbb{E}_{\mathbf{x}_0 \sim p(\mathbf{x}_0)} \left[ V_{soft}^\pi (\mathbf{x}_0) \right] \]
위 관계식은 표준 상태가치 함수와 목적함수 관계식과 형식적으로는 동일하다.
한편 소프트 상태가치 함수 식을 전개하면 다음과 같이 된다.
\[ \begin{align} V_{soft}^\pi (\mathbf{x}_t ) & = \mathbb{E}_{\tau_{u_t:u_T} \sim p(\tau_{u_t:u_T } | \mathbf{x}_t ) } \left[ -\alpha \log \pi( \mathbf{u}_t | \mathbf{x}_t ) + \sum_{k=t}^T \gamma^{k-t} \left( r_k -\gamma \alpha \log \pi (\mathbf{u}_{k+1} | \mathbf{x}_{k+1} ) \right) \right] \\ \\ & = \int_{\tau_{u_t:u_T}} -\alpha \log \pi (\mathbf{u}_t | \mathbf{x}_t ) p(\tau_{u_t:u_T} | \mathbf{x}_t ) d \tau_{u_t:u_T} \\ \\ & \ \ \ \ \ + \int_{\tau_{u_t:u_T}} \sum_{k=t}^T \gamma^{k-t} \left( r_k - \gamma \alpha \log \pi (\mathbf{u}_{k+1} | \mathbf{x}_{k+1} ) \right) p(\tau_{u_t:u_T } | \mathbf{x}_t ) d \tau_{u_t:u_T} \\ \\ & = \int_{\mathbf{u}_t} \int_{\tau_{x_{t+1}:u_T }} -\alpha \log \pi (\mathbf{u}_t | \mathbf{x}_t ) p( \tau_{x_{t+1}:u_T } | \mathbf{x}_t, \mathbf{u}_t ) \pi (\mathbf{u}_t | \mathbf{x}_t ) d \tau_{x_{t+1}:u_T} d\mathbf{u}_t \\ \\ & \ \ \ \ \ + \int_{\mathbf{u}_t} Q^\pi_{soft} (\mathbf{x}_t, \mathbf{u}_t ) d\mathbf{u}_t \\ \\ & = \mathbb{E}_{\mathbf{u}_t \sim \pi (\mathbf{u}_t | \mathbf{x}_t )} \left[ -\alpha \log \pi (\mathbf{u}_t | \mathbf{x}_t ) +Q_{soft}^\pi (\mathbf{x}_t, \mathbf{u}_t) \right] \end{align} \]
여기서
\[ \begin{align} Q_{soft}^\pi (\mathbf{x}_t, \mathbf{u}_t ) &= \int_{\tau_{x_{t+1}:u_T }} \sum_{k=t}^T \gamma^{k-t} \left( r_k - \gamma \alpha \log \pi (\mathbf{u}_{k+1} | \mathbf{x}_{k+1} ) \right) \ p(\tau_{x_{t+1}:u_T } | \mathbf{x}_t, \mathbf{u}_t ) d \tau_{x_{t+1}:u_T } \\ \\ &= \mathbb{E}_{\tau_{x_{t+1}:u_T } \sim p(\tau_{x_{t+1}:u_T} | \mathbf{x}_t, \mathbf{u}_t ) } \left[ \sum_{k=t}^T \gamma^{k-t} \left( r_k - \gamma \alpha \log \pi (\mathbf{u}_{k+1} | \mathbf{x}_{k+1}) \right) \right] \end{align} \]
는 표준 행동가치 함수에 엔트로피를 추가한 것으로서 소프트 행동가치 함수(soft action-value function)라고 한다. \(\tau_{x_{t+1}:u_T } = ( \mathbf{x}_{t+1}, \mathbf{u}_{t+1}, ... , \mathbf{u}_T)\) 는 상태변수 \( \mathbf{x}_t \) 에서 행동 \(\mathbf{u}_t\) 를 선택하고 그로부터 어떤 정책 \(\pi\) 로 생성되는 궤적이다.
정리하면 최대 엔트로피 목적함수에 적합하게 수정된 소프트 가치함수는 다음과 같다.
\[ \begin{align} & V_{soft}^\pi (\mathbf{x}_t) = \mathbb{E}_{\tau_{u_t:u_T } \sim p(\tau_{u_t:u_T} | \mathbf{x}_t) } \left[ \sum_{k=t}^T \gamma^{k-t} \left( r_k - \alpha \log \pi (\mathbf{u}_k | \mathbf{x}_k) \right) \right] \\ \\ & Q_{soft}^\pi (\mathbf{x}_t, \mathbf{u}_t ) = \mathbb{E}_{\tau_{x_{t+1}:u_T } \sim p(\tau_{x_{t+1}:u_T} | \mathbf{x}_t, \mathbf{u}_t ) } \left[ \sum_{k=t}^T \gamma^{k-t} \left( r_k - \gamma \alpha \log \pi (\mathbf{u}_{k+1} | \mathbf{x}_{k+1}) \right) \right] \end{align} \]
그리고 소프트 상태가치 함수와 행동가치 함수의 관계식은 다음과 같다.
\[ V_{soft}^\pi (\mathbf{x}_t ) = \mathbb{E}_{\mathbf{u}_t \sim \pi (\mathbf{u}_t | \mathbf{x}_t ) } \left[ Q_{soft}^\pi (\mathbf{x}_t, \mathbf{u}_t) - \alpha \log \pi (\mathbf{u}_t | \mathbf{x}_t ) \right] \]
\( \alpha=0\) 이면 소프트 가치함수는 표준 가치함수로 환원된다.
'AI 딥러닝 > RL' 카테고리의 다른 글
| 소프트 정책 이터레이션 (0) | 2021.05.28 |
|---|---|
| 소프트 벨만 방정식 (Soft Bellman Equation) (0) | 2021.05.27 |
| Tensorflow2로 만든 DDPG 코드: Pendulum-v0 (0) | 2021.05.14 |
| DQN에서 DDPG로 (0) | 2021.05.14 |
| Tensorflow2로 만든 Double DQN 코드: CartPole-v1 (0) | 2021.05.11 |




댓글