DQN 알고리즘에서는 상태변수가 연속공간 값이지만 행동은 이산공간 값으로 가정한다. 행동의 개수가 적으면 문제가 되지 않을 수도 있지만, 드론이나 로봇과 같은 실제 물리 시스템의 경우 행동의 차원이 크기 때문에 연속공간 값으로 가정하는 것이 더 타당하다.
그렇다면 DQN 알고리즘을 연속공간 상태변수와 행동의 경우에도 적용할 수 있을까.
먼저 DQN 알고리즘의 핵심인 정책과 시간차 타깃을 계산하는 부분을 살펴보자. 여기서는 상태변수와 행동을 모두 연속공간 값으로 가정하므로 상태변수는 \(\mathbf{x}_t\) 로 표기하고 행동은 \(\mathbf{u}_t\) 로 표기한다.
DQN은 확정적 정책을 가지며 다음과 같이 계산했다.
\[ \pi (\mathbf{x}_t )= \mathbf{u}_t =\arg\max_{\mathbf{u}_t} Q_\phi (\mathbf{x}_t, \mathbf{u}_t) \]
그리고 시간차 타깃 \(y_i\) 는 다음과 같이 계산했다.
\[ y_i = r(\mathbf{x}_i, \mathbf{u}_i )+ \gamma \max_{\mathbf{u}^\prime } Q_{\phi^\prime} (\mathbf{x}_{i+1}, \mathbf{u}^\prime ) \]
여기서 \(\phi\) 는 Q 신경망의 파라미터, \(\phi^\prime\) 는 타깃 신경망의 파라미터이고 \(Q_\phi \) 는 최적 행동가치 함수 \(Q^\star\) 의 값을 신경망으로 추정한 값이다.
연속공간 행동일 경우 DQN 알고리즘에서 문제가 되는 부분은 \(\max\) 와 \(\arg\max\) 연산자이다. 이들 연산자는 학습 시 이터레이션 루프 안에 포함되므로 매 이터레이션 마다 최적화 계산을 수행해야 하는 문제가 있다.
이에 대한 해결책으로는 행동을 무작위로 샘플링 한 후, 그 중에서 가장 큰 Q 값을 선택하는 확률 최적화(stochastic optimization) 방법, 행동가치 함수를 최적화하기 편리한 구조(예를 들면 2차함수)로 고정하는 방법 등이 있을 수 있다.
하지만 DDPG 알고리즘에서는 이에 대한 해결책으로서 \(\theta\) 로 파라미터화된 액터(actor) 신경망을 도입하여 정책을 다음과 같이 근사하는 새로운 방법을 제안했다.
\[ \pi_\theta (\mathbf{x}_t ) \approx \arg\max_{\mathbf{u}_t} Q_\phi (\mathbf{x}_t, \mathbf{u}_t) \]
DDPG는 deep deterministic policy gradient(심층 확정적 정책 그래디언트)의 약자로서, 이름에서도 알 수 있듯이 본래 정책 그래디언트 방법을 사용하여 확정적 정책을 계산하는 정책 그래디언트 계열의 알고리즘이다. 하지만 DQN을 연속공간 행동으로 확장한 Q-러닝 계열의 알고리즘으로 보기도 한다.
액터 신경망의 파라미터는 다음 최적화 식을 만족해야 하므로,
\[ \theta^\star = \arg\max_\theta Q_\phi (\mathbf{x}_t, \pi_\theta (\mathbf{x}_t )) \]
\(Q_\phi\) 를 최대화하는 파라미터 \(\theta\) 는 다음과 같이 경사상승법으로 구할 수 있다.
\[ \theta \gets \theta + \alpha \nabla_\theta Q_\phi (\mathbf{x}_t, \pi_\theta (\mathbf{x}_t )) \]
여기서 \(Q_\phi\) 의 \(\theta\) 에 대한 그래디언트 \(\nabla_\theta Q_\phi (\mathbf{x}_t, \pi_\theta (\mathbf{x}_t ))\) 는 원래 DDPG를 처음 제안한 논문에서와 같이 다음과 같은 연쇄법칙으로 표현할 수도 있다.
\[ \begin{align} \nabla_\theta Q_\phi &= \frac{dQ_\phi}{d \theta}= \frac{d \mathbf{u}_t}{d \theta} \frac{dQ_\phi}{d \mathbf{u}_t} \\ \\ &= \nabla_\theta \pi_\theta (\mathbf{x}_t ) \nabla_{\mathbf{u}_t} Q_\phi (\mathbf{x}_t, \mathbf{u}_t) \end{align} \]
시간차 타깃 \(y_i\) 는 타깃(target) Q 신경망을 이용하여 계산하는데,
\[ \begin{align} y_i & = r(\mathbf{x}_i, \mathbf{u}_i )+ \gamma \max_{\mathbf{u}_{i+1}} Q_{\phi^\prime} (\mathbf{x}_{i+1}, \mathbf{u}_{i+1 } ) \\ \\ & = r(\mathbf{x}_i, \mathbf{u}_i )+ \gamma Q_{\phi^\prime} (\mathbf{x}_{i+1}, \arg\max_{\mathbf{u}_{i+1}} Q_{\phi^\prime} (\mathbf{x}_{i+1}, \mathbf{u}_{i+1 } ) \\ \\ & \approx r( \mathbf{x}_i, \mathbf{u}_i ) + \gamma Q_{\phi^\prime } (\mathbf{x}_{i+1}, \pi_{\theta^\prime} (\mathbf{x}_{i+1 } )) \end{align} \]
이 때 필요한 행동 \(\pi_{\theta^\prime} (\mathbf{x}_{i+1 } )\) 도 \(\theta^\prime\) 로 파라미터화된 타깃 액터 신경망을 별도로 도입하여 계산한다.
액터 신경망의 손실함수는 그래디언트 \(\nabla_\theta Q_\phi (\mathbf{x}_t, \pi_\theta (\mathbf{x}_t ))\) 를 고려하여 다음과 같이 정하면 된다.
\[ L(\theta)= -\sum_i Q_\phi (\mathbf{x}_t, \pi_\theta (\mathbf{x}_t )) \]
여기서 마이너스 부호가 붙은 이유는 신경망은 손실함수를 최소화하도록 파라미터가 업데이트되는 반면, DDPG 알고리즘은 \(Q_\phi\) 를 최대로 해야 하기 때문이다.
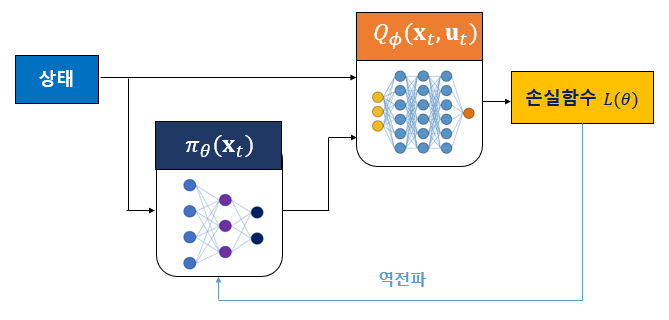
Q 신경망의 손실함수는 다음과 같다. DDPG에서는 Q 신경망을 크리틱(critic) 신경망이라고 한다.
\[ L(\phi)=\frac{1}{2} \sum_i \lVert y_i-Q_\phi (\mathbf{x}_i, \mathbf{u}_i) \rVert^2 \]
여기서 \( y_i = r( \mathbf{x}_i, \mathbf{u}_i ) + \gamma Q_{\phi^\prime } (\mathbf{x}_{i+1}, \pi_{\theta^\prime} (\mathbf{x}_{i+1 } )) \) 이다.

DDPG에서는 타깃 신경망의 파라미터가 원래 신경망의 파라미터를 느린 속도로 따라가는 방법을 사용한다.
\[ \begin{align} & \theta^\prime \gets \tau \theta + (1-\tau) \theta^\prime \\ \\ & \phi^\prime \gets \tau \phi + (1-\tau) \phi^\prime \end{align} \]
여기서 \(\tau\) 는 아주 작은 값으로 설정한다.
DDPG도 확정적 정책이므로 DQN과 같은 탐색(exploration)의 문제가 발생한다. DQN에서는 이러한 문제를 해결하고자 \(\epsilon -\)탐욕(greedy) 탐색 방법을 사용했지만, DDPG에서는 행동에 노이즈(noise) \(\eta_t\) 를 도입함으로써 간단히 해결했다.
\[ \pi_{noisy} (\mathbf{x}_t )= \pi_\theta (\mathbf{x}_t )+\eta_t \]
DDPG 알고리즘을 최종 정리하면 다음과 같다.
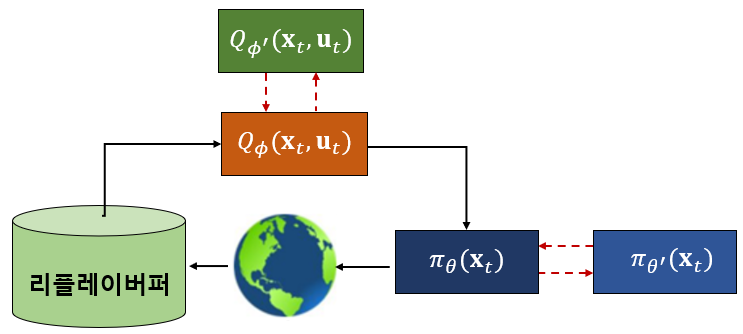
[1] 크리틱과 액터 신경망의 파라미터를 초기화한다.
[2] 크리틱과 액터 신경망의 파라미터를 타깃 신경망에 복사한다.
[3] 리플레이 버퍼를 초기화 한다. 그리고 [4]-[9]를 반복한다.
[4] 정책을 실행하여 발생된 천이샘플(transition sample) \(\{\mathbf{x}_i, \mathbf{u}_i, r_i, \mathbf{x}_{i+1}\}\) 를 리플레이 버퍼에 저장한다.
[5] 리플레이 버퍼에서 \(N\) 개의 천이샘플 \(\{\mathbf{x}_i, \mathbf{u}_i, r_i, \mathbf{x}_{i+1}\}\) 를 무작위로 추출한다.
[6] \(y_i = r( \mathbf{x}_i, \mathbf{u}_i ) + \gamma Q_{\phi^\prime } (\mathbf{x}_{i+1}, \pi_{\theta^\prime} (\mathbf{x}_{i+1 } )) \) 를 계산한다.
[7] \( L(\phi)=\frac{1}{2} \sum_i \lVert y_i-Q_\phi (\mathbf{x}_i, \mathbf{u}_i) \rVert^2 \) 로 크리틱 신경망을 업데이트 한다.
[8] \( L(\theta)= -\sum_i Q_\phi (\mathbf{x}_t, \pi_\theta (\mathbf{x}_t )) \) 로 액터 신경망을 업데이트 한다.
[9] 타깃 크리틱과 타깃 액터 신경망을 업데이트 한다.
'AI 딥러닝 > 강화학습' 카테고리의 다른 글
| 최대 엔트로피 목적함수 (0) | 2021.05.26 |
|---|---|
| Tensorflow2로 만든 DDPG 코드: Pendulum-v0 (0) | 2021.05.14 |
| Tensorflow2로 만든 Double DQN 코드: CartPole-v1 (0) | 2021.05.11 |
| Double DQN 알고리즘 (0) | 2021.05.11 |
| Tensorflow2로 만든 DQN 코드: CartPole-v1 (0) | 2021.05.04 |




댓글