한 개의 샘플을 이용한 목적함수의 그래디언트는 다음과 같았다.
\[ \nabla_\theta J(\theta) \approx \sum_{t=0}^T \left[ ( \nabla_\theta \log \pi_\theta (\mathbf{u}_t | \mathbf{x}_t)) A^{\pi_\theta} (\mathbf{x}_t, \mathbf{u}_t ) \right] \]
앞에서 크리틱 신경망을 설계했으므로 수식 안에 있는 어드밴티지 함수는 크리틱 신경망의 추정값으로 대체한다.
\[ \nabla_\theta J(\theta) \approx \sum_{t=0}^T \left[ ( \nabla_\theta \log \pi_\theta (\mathbf{u}_t | \mathbf{x}_t)) \hat{A} (\mathbf{x}_t, \mathbf{u}_t ) \right] \]
이제 \(\theta\)로 파라미터화된 정책 신경망을 학습할 수 있는 방법을 고안해 보자. 정책 신경망을 액터(actor) 신경망이라고도 한다.
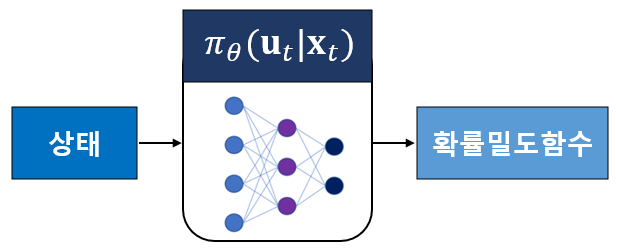
먼저 고려해야 할 점은 액터 신경망의 출력인 \(\pi_\theta (\mathbf{u}_t | \mathbf{x}_t )\)에 관한 것이다.
연속공간 행동(action)이라면 정책 \(\pi_\theta (\mathbf{u}_t | \mathbf{x}_t )\)는 확률밀도함수가 되므로 정책 신경망 출력 레이어의 뉴런이 무한개가 필요하다. 따라서 구현 가능한 신경망을 만들기 위해서는 정책 확률밀도함수\(\pi_\theta (\mathbf{u}_t | \mathbf{x}_t )\)를 특정 구조로 가정하는 것이 필요하다.
일반적으로 정책 확률밀도함수를 기댓값이 \(\mu=[ \mu_1 \ \mu_2 \ \cdots \ \mu_m ]^T\), 공분산이 \(P=diag \{ \sigma_1^2, \ \sigma_2^2, \ ..., \ \sigma_m^2 \}\)인 가우시안으로 가정한다.
\[ \begin{align} \pi_\theta (\mathbf{u}_t | \mathbf{x}_t ) &= \frac{1}{ \sqrt{(2\pi)^m \det P_\theta } } \exp \left( -\frac{1}{2} ( \mathbf{u}_t-\mu_\theta (\mathbf{x}_t ) )^T P_\theta^{-1} ( \mathbf{u}_t-\mu_\theta (\mathbf{x}_t ) ) \right) \\ \\ &= \prod_{j=1}^m \pi_\theta (u_{t,j} | \mathbf{x}_t) \end{align} \]
여기서 \(\det P_\theta \)는 \(P_\theta\)의 행렬식(determinant), \(u_{t,j}\)는 \(\mathbf{u}_t\)의 \(j\)번째 성분이며,
\[ \pi_\theta (u_{t,j} | \mathbf{x}_t ) = \frac{1}{ \sqrt{ 2\pi \sigma^2_{\theta, j} (\mathbf{x}_t) } } \exp \left( - \frac{ ( u_{t,j}-\mu_{\theta, j} (\mathbf{x}_t ) )^2 }{ 2 \sigma^2_{\theta, j } (\mathbf{x}_t)} \right) \]
이다. 따라서 \(\log \pi_\theta (\mathbf{u}_t | \mathbf{x}_t) \)는 다음과 같이 계산된다.
\[ \begin{align} \log \pi_\theta (\mathbf{u}_t | \mathbf{x}_t ) &= \sum_{j=1}^m \log \pi_\theta (u_{t,j} | \mathbf{x}_t) \\ \\ &= - \sum_{j=1}^m \left[ \frac{1}{2} \log ( 2\pi \sigma^2_{\theta, j} (\mathbf{x}_t) ) + \frac{ ( u_{t,j}-\mu_{\theta, j} (\mathbf{x}_t ) )^2 }{ 2 \sigma^2_{\theta, j } (\mathbf{x}_t)} \right] \end{align} \]
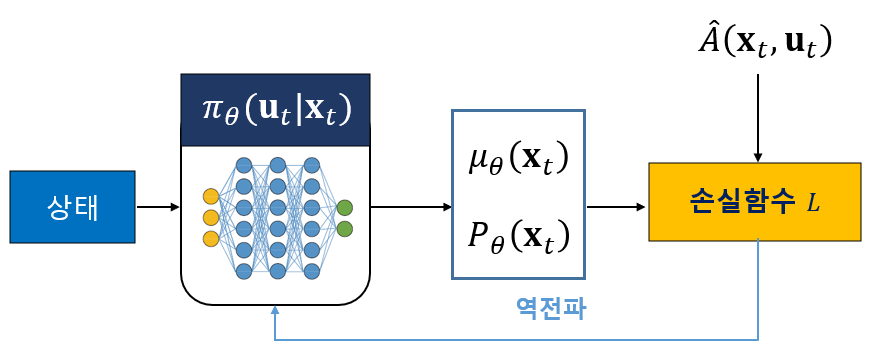
이제 액터 신경망의 출력은 평균 \(\mu_\theta (\mathbf{x}_t )\)와 공분산 \(P_\theta\)가 된다.
다음으로 정책이 목적함수를 최대화하는 파라미터 \(\theta\)를 갖도록 학습할 수 있는 손실함수를 정해야 한다. 목적함수의 그래디언트에서
\[ \nabla_\theta J(\theta) \approx \sum_{t=0}^T \left[ ( \nabla_\theta \log \pi_\theta (\mathbf{u}_t | \mathbf{x}_t)) \hat{A} (\mathbf{x}_t, \mathbf{u}_t ) \right] \]
\(\hat{A} (\mathbf{x}_t, \mathbf{u}_t )\)는 \(\theta\)의 함수가 아니므로 그래디언트 안에 포함될 수 있다.
\[ \nabla_\theta J(\theta) \approx \nabla_\theta \left[ \sum_{t=0}^T \left[ \log ( \pi_\theta (\mathbf{u}_t | \mathbf{x}_t)) \hat{A} (\mathbf{x}_t, \mathbf{u}_t ) \right] \right] \]
따라서 액터 신경망의 손실함수를 다음과 같이 정하면 된다.
\[ L(\theta) = - \sum_{i} \left[ \log ( \pi_\theta (\mathbf{u}_i | \mathbf{x}_i)) \hat{A} (\mathbf{x}_i, \mathbf{u}_i ) \right] \]
여기서 마이너스 부호가 붙은 이유는 신경망은 손실함수를 최소화하도록 파라미터가 업데이트되는 반면, 강화학습 알고리즘은 목적함수를 최대로 해야 하기 때문이다.
이와 같이 어드밴티지 함수를 이용하는 액터 신경망과 크리틱 신경망을 이용하여 목적함수를 최대화하는 강화학습 알고리즘을 Advantage Actor Critic 또는 A2C 알고리즘이라고 한다.
알고리즘을 정리하면 다음과 같다.
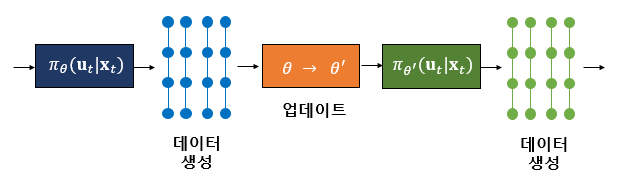
[1] 크리틱과 액터 신경망의 파라미터를 초기화한다. 그리고 [2]-[5]를 반복한다.
[2] 정책 \(\pi_\theta (\mathbf{u}_t | \mathbf{x}_t )\)를 실행하여 천이샘플(transition sample) \(\{\mathbf{x}_i, \mathbf{u}_i, r_i, \mathbf{x}_{i+1} \}\)를 모은다.
[3] \(V_\phi (\mathbf{x}_t, \mathbf{u}_t )\)를 추정한다.
[4] \(\hat{A} (\mathbf{x}_t, \mathbf{u}_t ) = r( \mathbf{x}_t, \mathbf{u}_t )+ \gamma V_\phi (\mathbf{x}_{t+1} )-V_\phi (\mathbf{x}_t ) \)를 계산한다.
[5] \( \theta \gets \theta - \alpha \nabla_\theta \sum_i \left[ \log( \pi_\theta (\mathbf{u}_i | \mathbf{x}_i ) ) \hat{A}(\mathbf{x}_i, \mathbf{u}_i ) \right] \)로 신경망을 업데이트 한다.
'AI 딥러닝 > RL' 카테고리의 다른 글
| 가치함수 (Value Function) (0) | 2021.04.21 |
|---|---|
| Tensorflow2로 만든 A2C 코드: Pendulum-v0 (0) | 2021.04.20 |
| A2C 알고리즘-1: 크리틱 신경망 (0) | 2021.04.20 |
| 정책 그래디언트 기반 강화학습의 원리 (0) | 2021.04.13 |
| 강화학습 문제 (0) | 2020.11.08 |




댓글