Extended Yale Face Database B 라는 얼굴 사진을 잔뜩 모아 놓은 사이트가 있다.
http://vision.ucsd.edu/~iskwak/ExtYaleDatabase/ExtYaleB.html
38명의 사람 얼굴을 9개의 자세 및 64개의 서로 다른 조명 조건에서 촬영한 사진으로 구성 되어있는데 Cropped Images에 있는 사진들은 높이가 192 픽셀 너비가 168픽셀로 된 흑백 사진이다. 이 얼굴 사진들은 연구 목적으로 자유롭게 사용할 수 있다.
PCA 알고리즘을 얼굴 사진 라이브러리에 적용하여 이른바 eigenfaces라는 축소 차원 좌표축을 구하고 사진 데이터를 eigenfaces로 표현하고 또 복원해 보도록 하자.
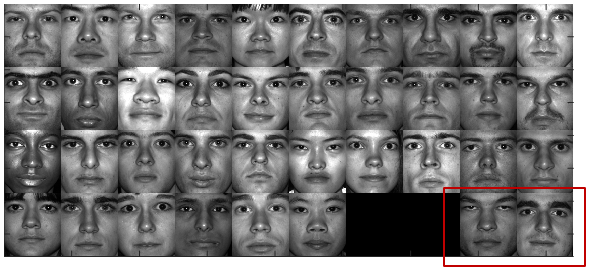
먼저 36명의 정면 얼굴 사진만을 추출하여 스냅샷 행렬을 만든다. 아래 그림에서 빨강색 박스로 표시된 나머지 2명의 얼굴은 평가용으로 남겨두고자 한다.
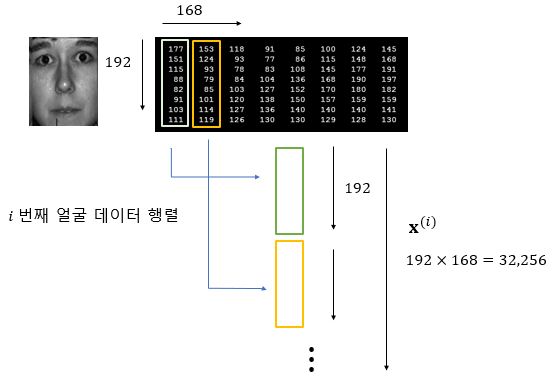
얼굴 데이터는 \(192 \times 168\) 행렬로 되어 있으므로 벡터로 바꾸어야 한다. 얼굴 데이터 행렬에서 열(column)단위로 쌓아가면 32,256 차원을 갖는 벡터 \(\mathbf{x}^{(i)}\)를 만들 수 있다.
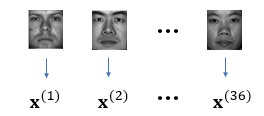
36명의 얼굴 사진에 대해서 차례로 데이터셋 \(\mathbf{x}^{(1)}, \mathbf{x}^{(2)}, ..., \mathbf{x}^{(36)} \in \mathbb{R}^{32,256}\)을 만든다.
이제 PCA 알고리즘의 절차를 밟는다. 코드는 매트랩으로 작성했다.
(1) 데이터셋의 샘플 평균을 계산한다.
\[ \mathbf{\mu} = \frac{1}{m} \sum_{i=1}^m \mathbf{x}^{(i)} \]
X = yaleFace(:, 1:36); % 32,256 by 36
mu = mean(X,2);
평균 얼굴 모습은 다음과 같다.
figure(1), axes('position',[0 0 1 1]), axis off
imagesc(reshape(mu,n,m)), colormap gray

(2) 모든 데이터셋을 다음과 같이 치환한다.
\[ \mathbf{y}^{(i)} = \mathbf{x}^{(i)} - \mathbf{\mu} \]
(3) 데이터셋의 스냅샷 행렬을 만든다.
\[ Y= \begin{bmatrix} \mathbf{y}^{(1) } & \mathbf{y}^{(2) } & \cdots & \mathbf{y}^{(m) } \end{bmatrix} \ \in \mathbb{R}^{n \times m} \]
Y = X - mu;
(4) 스냅샷 행렬 \(Y\)의 특이값 분해(SVD, singular value decomposition)를 계산한다.
\[ Y=U \Sigma V^T \]
[U, S, V] = svd(Y, 'econ');
특이값을 순서대로 나열해서 그림으로 보이면 다음과 같다.
Sd = diag(S);
figure(2), stem(Sd, 'o')
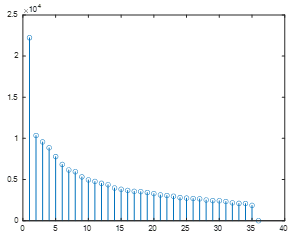
(5) d차원 (\( d \lt n\)) 직교 좌표축 \(\mathbf{w}_i, \ i=1, ...,d\) 를 선택한다.
\[ \begin{align} W &= \begin{bmatrix} \mathbf{w}_1 & \mathbf{w}_2 & \cdots & \mathbf{w}_d \end{bmatrix} \\ \\ &= \begin{bmatrix} \mathbf{u}_1 & \mathbf{u}_2 & \cdots & \mathbf{u}_d \end{bmatrix} = U_d \ \in \mathbb{R}^{n \times d} \end{align}\]
축소 차원 \(d\)는 특이값을 이용하여 설계자가 미리 설정한 투사 오차보다 작도록 선정하면 된다.
다음 그림은 첫번째와 두번째 좌표축(여기서는 eigenfaces)을 이미지 데이터 \(192 \times 168\)로 재변환하여 나타낸 것이다.
figure(3), axes('position',[0 0 1 1]), axis off
imagesc(reshape(U(:,1),n,m)), colormap gray
figure(4), axes('position',[0 0 1 1]), axis off
imagesc(reshape(U(:,2),n,m)), colormap gray

(6) 좌표축 \(\mathbf{w}_i, \ i=1, ..., d\) 의 축성분을 계산한다.
\[ \mathbf{z}_i= U_d^T ( \mathbf{x}^{(i)} - \mathbf{\mu} ) \]
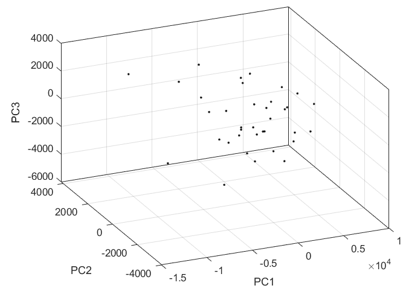
다음 그림은 3차원으로 축소했을 때 36개의 얼굴 데이터의 축성분을 표시한 것이다.
d = 3;
Z = U(:,1:d)'*Y;
figure(5),plot3(Z(1,:),Z(2,:), Z(3,:),'k.','LineWidth',2)
box, grid
xlabel('PC1'); ylabel('PC2'); zlabel('PC3')
(7) 차원이 축소된 좌표계에서 원래 차원의 좌표계로 데이터를 복원시키려면 다음과 같이 계산한다.
\[ \hat{\mathbf{x}}^{(i)} = \mathbf{\mu} + U_d \mathbf{z}_i \]
다음 그림은 첫번째 얼굴을 20차원으로 축소시킨 후 다시 원래 얼굴로 복원시킨 것이다.
d=20;
num_face = 1;
original_face = yaleFace(:, num_face);
y_test = original_face - mu;
P_til = mu + U(:,1:d)*U(:,1:d)'*y_test;
figure(6), axes('position',[0 0 1 1]), axis off
imagesc(reshape(original_face,n,m)), colormap gray
figure(7), axes('position',[0 0 1 1]), axis off
imagesc(reshape(P_til,n,m)), colormap gray

다음 그림은 첫번째 얼굴을 36차원으로 축소시킨 후 다시 원래 얼굴로 복원시킨 것이다. 원본과 구별할 수 없을 정도로 정확하다.

다음 그림은 eigenfaces을 계산할 때 사용하지 않은 데이터인 37번째 얼굴을 36차원으로 축소시킨 후 다시 원래 얼굴로 복원시킨 것이다.

원본과 비교하여 상당한 차이가 있는 것을 알 수 있다. 아무래도 32,256 차원의 이미지 공간을 36개의 eigenfaces로 표현하자니 일반적인 얼굴을 표현하는데에 한계가 있는 것으로 보인다. 하지만 Extended Yale Face Database B에 있는 38명의 사람 얼굴을 9개의 자세 및 64개의 서로 다른 조명 조건에서 촬영한 사진을 모두 사용하여 2,000 여개 이상의 eigenfaces를 구축한다면 보다 정확한 복원이 가능할 것으로 보인다.
'유도항법제어 > 데이터기반제어' 카테고리의 다른 글
| [POD-2] 스냅샷 적합직교분해 (snapshot POD) (0) | 2021.03.01 |
|---|---|
| [POD-1] 고전 적합직교분해 (classical POD) (0) | 2021.02.28 |
| [PCA–3] 주성분 분석 (PCA) 특징 (0) | 2021.02.20 |
| [PCA–2] 주성분 분석 (PCA) 알고리즘 유도 (0) | 2021.02.19 |
| [PCA–1] 주성분 분석 (PCA) (0) | 2021.02.18 |




댓글