[PCA–3] 주성분 분석 (PCA) 특징

n차원 공간 상의 m개 데이터 ${\mathbf{x}}^{(1)},{\mathbf{x}}^{(2)},...,{\mathbf{x}}^{(m)}\in {\mathbb{R}}^n$ 에 대한 주성분 분석(PCA) 알고리즘을 정리하면 다음과 같다.

 

 

(1) 데이터셋의 샘플 평균을 계산한다.

 

$$\mu =\frac{1}{m}\sum _{i=1}^m{\mathbf{x}}^{(i)}$$

 

(2) 모든 데이터셋을 다음과 같이 치환한다.

 

$${\mathbf{y}}^{(i)}={\mathbf{x}}^{(i)}-\mu$$

 

(3) 데이터셋의 스냅샷(snapshot) 행렬을 만든다.

 

$$Y=\left[\begin{array}{cccc}{\mathbf{y}}^{(1)}& {\mathbf{y}}^{(2)}& \cdots & {\mathbf{y}}^{(m)}\end{array}\right]\in {\mathbb{R}}^{n\times m}$$

 

(4) 스냅샷 행렬 $Y$의 특이값 분해(SVD, singular value decomposition)를 계산한다.

 

$$\begin{array}{rl}Y& =U\mathrm{\Sigma }{V}^T\\ \\ U=\left[\begin{array}{ccc}{\mathbf{u}}_1& \cdots & {\mathbf{u}}_n\end{array}\right]\in {\mathbb{R}}^{n\times n},& V=\left[\begin{array}{ccc}{\mathbf{v}}_1& \cdots & {\mathbf{v}}_m\end{array}\right]\in {\mathbb{R}}^{m\times m}\end{array}$$

 

(5) d차원 ($d<n$) 직교 좌표축 ${\mathbf{w}}_i,i=1,...,d$ 를 선택한다.

 

$$\begin{array}{rl}W& =\left[\begin{array}{cccc}{\mathbf{w}}_1& {\mathbf{w}}_2& \cdots & {\mathbf{w}}_d\end{array}\right]\\ \\ & =\left[\begin{array}{cccc}{\mathbf{u}}_1& {\mathbf{w}}_2& \cdots & {\mathbf{u}}_d\end{array}\right]=U_d\in {\mathbb{R}}^{n\times d}\end{array}$$

 

(6) 좌표축 ${\mathbf{w}}_i,i=1,...,d$ 의 축성분을 계산한다.

 

$${\mathbf{z}}_i=U_d^T({\mathbf{x}}^{(i)}-\mu )$$

 

(7) 차원이 축소된 좌표계에서 원래 차원의 좌표계로 데이터를 복원시키려면 다음과 같이 계산한다.

 

$${\hat{\mathbf{x}}}^{(i)}=\mu +U_d{\mathbf{z}}_i$$

 

 

 

주성분 분석(PCA)의 특징을 살펴보자.

우선 주성분 분석(PCA)은 투사 오차(prediction error)를 최소화하도록 축소 차원의 좌표축 벡터인 ${\mathbf{w}}_1,{\mathbf{w}}_2,...,{\mathbf{w}}_d$ 를 결정하는 알고리즘이다. 그런데 투사 오차를 최소화하는 것은 곧 투사 분산을 최대화하는 것과 동일하다. 즉 데이터가 더 넓게 분포된 방향으로 좌표축이 정해진다. 이에 대해서 수식으로 알아보자.

행렬 $Y{Y}^T$의 고유값 ${\sigma }_i^2$과 고유벡터 ${\mathbf{u}}_i$는 특이값 분해를 이용하여 다음과 같이 구할 수 있었다.

 

$$Y{Y}^T{\mathbf{u}}_i={\sigma }_i^2{\mathbf{u}}_i,i=1,...,n$$

 

여기서 ${\mathbf{u}}_i$는 PCA에서 축소 차원의 좌표축으로 설정한 서로 직각인 단위 벡터고 ${\sigma }_i^2$는 큰 수에서 작은 수의 순서로 정렬시킨 고유값이다. 위 식에서 행렬 $Y{Y}^T$를 전개해보면 다음과 같이 된다.

 

$$\begin{array}{rl}Y{Y}^T& =\left[\begin{array}{ccc}{\mathbf{y}}^{(1)}& \cdots & {\mathbf{y}}^{(m)}\end{array}\right]\left[\begin{array}{c}({\mathbf{y}}^{(1)}{)}^T\\ ⋮\\ ({\mathbf{y}}^{(m)}{)}^T\end{array}\right]\\ \\ & =\sum _{i=1}^m{\mathbf{y}}^{(i)}({\mathbf{y}}^{(i)}{)}^T\end{array}$$

 

즉 행렬 $Y{Y}^T$는 데이터셋의 샘플 분산(정확히는 $\frac{1}{m-1}Y{Y}^T$이 샘플 분산이다)이므로 행렬 $Y{Y}^T$의 고유값과 고유벡터는 샘플 분산의 고유값과 고유벡터이다. 이것으로 축소 차원의 좌표축은 데이터가 더 넓게 분포된 방향으로 정해진다는 것을 알 수 있다. PCA에서 주성분이라 함은 데이터의 분산이 가장 큰 방향을 의미한다.

 

 

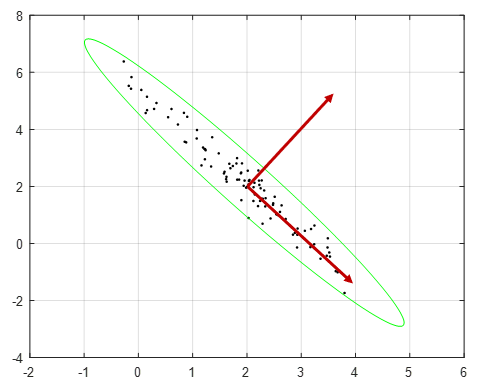
둘째, 축소 차원으로 표현된 데이터 ${\mathbf{z}}_i$는 서로 비상관(uncorrelated) 관계에 있다. 참고로 ${\mathbf{z}}_i$를 특징(feature)벡터라고도 한다. 수식으로 알아보기 위해서 ${\mathbf{z}}_i$의 샘플 분산을 계산해 보자.

 

$$\begin{array}{rl}\sum _{i=1}^m{\mathbf{z}}_i{\mathbf{z}}_i^T& =\sum _{i=1}^m{U}_d^T({\mathbf{x}}^{(i)}-\mu ){({\mathbf{x}}^{(i)}-\mu )}^T{U}_d\\ \\ & =U_d^T(\sum _{i=1}^m({\mathbf{x}}^{(i)}-\mu )({\mathbf{x}}^{(i)}-\mu {)}^T)U_d\\ \\ & =U_d^{T}Y{Y}^T{U}_d\\ \\ & =U_d^{T}U{\mathrm{\Sigma }}^2{U}^T{U}_d\\ \\ & =\left[\begin{array}{cc}{I}_d& 0\end{array}\right]{\mathrm{\Sigma }}^2\left[\begin{array}{c}{I}_d\\ 0\end{array}\right]\\ \\ & ={\mathrm{\Sigma }}_d^2\end{array}$$

 

${\mathbf{z}}_i$의 샘플 분산이 대각 행렬로 나오므로 ${\mathbf{z}}_i$는 서로 비상관 관계에 있다는 것을 알 수 있다. 즉 PCA는 서로 연관 가능성이 있는 고차원 데이터를 서로 비상관 관계에 있는 저차원 데이터로 변환시켜준다.

PCA 알고리즘의 (3)에서 스냅샷 행렬은 n차원 공간상의 m개 데이터로 구성된다. 일반적인 영상 데이터나 물리 시스템의 실험 또는 시뮬레이션 데이터(예를 들면 CFD 데이터) 등은 차원 n이 매우 크다(예를 들면 ${10}^9$ 정도). 반면에 데이터 수 m은 데이터의 차원에 비해서 상당히 작은 경우가 많다(예를 들면 ${10}^4$ 정도). 이 경우에는 특이값 분해를 통하여 특이값과 특이 벡터를 구하기가 어렵고 행렬 $Y{Y}^T\in {\mathbb{R}}^{n\times n}$의 고유값과 고유벡터를 통해 계산하기도 힘들다.

 

 

반면에 행렬 $Y^{T}Y\in {\mathbb{R}}^{m\times m}$은 사이즈가 작기 때문에 고유값과 고유벡터 계산이 상대적으로 쉽다. 행렬 $Y^{T}Y$의 고유값과 고유벡터를 이용하면 스냅샷 행렬 $Y$의 특이값과 왼쪽 특이벡터 ${\mathbf{u}}_i$를 쉽게 구할 수 있다.

 

 

행렬 $Y$의 특이값 분해 $Y=U\mathrm{\Sigma }{V}^T$로부터

 

$$Y{Y}^T{\mathbf{v}}_i={\sigma }_i^2{\mathbf{v}}_i,i=1,...,m$$

 

이 성립한다. 여기서 ${\mathbf{v}}_i$는 스냅샷 행렬 $Y$의 오른쪽 특이벡터이자 행렬 $Y^{T}Y$의 고유벡터이다. 한편 $Y=U\mathrm{\Sigma }{V}^T$로부터 $Y{\mathbf{v}}_i={\sigma }_i{\mathbf{u}}_i$이 성립하므로

 

$${\mathbf{u}}_i=\frac{Y{\mathbf{v}}_i}{{\sigma }_i},i=1,...,m$$

 

의 관계식을 얻을 수 있다. 위 두 식을 이용하여 스냅샷 행렬 $Y$의 왼쪽 특이벡터 ${\mathbf{u}}_i$와 특이값 ${\sigma }_i$를 계산해 낼 수 있다.