실수 대칭행렬의 고유값과 고유벡터

행렬의 성분이 모두 실수(real number)이고 대칭인 행렬을 실수 대칭행렬이라고 한다. 일반적인 행렬에서 고유값(eigenvalue)과 고유벡터(eigenvector)는 복소수 값을 가질 수 있다.

 

 

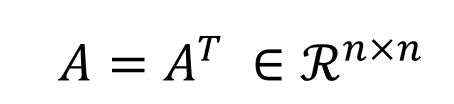
하지만 실수 대칭행렬의 고유값과 고유벡터는 모두 실수값이다. 또한 서로 다른 고유값에 해당하는 고유벡터는 서로 직각이다.
이를 증명해 보자.

 

 

먼저 $n\times n$ 정방 행렬 $A$의 고유값과 고유벡터는 다음과 같이 정의된다. 

 

$$\begin{array}{}\text{(1)}& A\mathbf{v}=\lambda \mathbf{v}\end{array}$$

 

여기서 $\lambda$는 고유값, $\mathbf{v}는$ 그에 해당하는 고유벡터다.
켤레 복소수를 사용하면 위 식은 다음과 같이 쓸 수 있다.

 

$$\begin{array}{}\text{(2)}& \overline{A}\overline{\mathbf{v}}=\overline{\lambda }\overline{\mathbf{v}}\end{array}$$

 

여기서 바(bar)는 켤레 복소수를 나타내는 기호이다. $A$는 실수 행렬이므로 위 식은 다음과 같이 된다.

 

$$\begin{array}{}\text{(3)}& A\overline{\mathbf{v}}=\overline{\lambda }\overline{\mathbf{v}}\end{array}$$

 

식 (3)에 의하면 $A$가 실수 행렬인 경우, $\lambda$와 $\mathbf{v}$가 고유값과 고유벡터이면 그 켤레 복소수와 켤레 복소벡터인 $\overline{\lambda }$와 $\overline{\mathbf{v}}$도 고유값과 고유벡터가 되는 것을 알 수 있다.

$A$는 또한 대칭 행렬 $A=A^T$이므로 위 식의 양변을 전치(transpose)하면 다음 식이 된다.

 

$$\begin{array}{}\text{(4)}& {\overline{\mathbf{v}}}^{T}A=\overline{\lambda }{\overline{\mathbf{v}}}^T\end{array}$$

 

이제 식 (1)의 양변에 ${\overline{\mathbf{v}}}^T$를 곱해보자. 그러면,

 

$$\begin{array}{}\text{(5)}& {\overline{\mathbf{v}}}^{T}A\mathbf{v}=\lambda {\overline{\mathbf{v}}}^T\mathbf{v}\end{array}$$

 

이 된다. 한편 식 (4)의 양변에 $\mathbf{v}$를 곱하면,

 

$$\begin{array}{}\text{(6)}& {\overline{\mathbf{v}}}^{T}A\mathbf{v}=\overline{\lambda }{\overline{\mathbf{v}}}^T\mathbf{v}\end{array}$$

 

이 된다. 식 (5)와 (6)은 같은 값을 가지므로 다음 식이 성립한다.

 

$$\begin{array}{}\text{(7)}& (\lambda -\overline{\lambda }){\overline{\mathbf{v}}}^{T}A\mathbf{v}=0\end{array}$$

 

따라서 

 

$$\begin{array}{}\text{(8)}& \lambda =\overline{\lambda }\end{array}$$

 

이 되므로 고유값은 실수값임이 증명되었다.

한편, 고유값과 고유벡터의 정의에서 

 

$$\begin{array}{}\text{(9)}& (A-\lambda I)\mathbf{v}=0\end{array}$$

 

$(A-\lambda I)$가 실수 행렬이므로 $\lambda$에 해당하는 고유벡터 $\mathbf{v}$도 실수 벡터가 되어야 한다.

고유값 $\lambda$에 해당하는 고유벡터를 $\mathbf{v}$, 고유값 $\mu$에 해당하는 고유벡터를 $\mathbf{w}$라고 하면, 정의에 의해서 다음 식이 성립한다. 

 

$$\begin{array}{}\text{(10)}& \begin{array}{rl}A\mathbf{v}& =\lambda \mathbf{v}\\ \\ A\mathbf{w}& =\mu \mathbf{w}\end{array}\end{array}$$

 

위 식의 양변의 각각 ${\mathbf{w}}^T$와 ${\mathbf{v}}^T$를 곱하면 다음과 같이 된다. 

 

$$\begin{array}{}\text{(11)}& \begin{array}{rl}{\mathbf{w}}^{T}A\mathbf{v}& =\lambda {\mathbf{w}}^T\mathbf{v}\\ \\ {\mathbf{v}}^{T}A\mathbf{w}& =\mu {\mathbf{v}}^T\mathbf{w}\end{array}\end{array}$$

 

위 두 식은 모두 스칼라이고 $A=A^T$이므로 두 개의 식은 같다. 즉, 

 

$$\begin{array}{}\text{(12)}& \begin{array}{rl}{\mathbf{v}}^{T}A\mathbf{w}& ={\mathbf{w}}^T{A}^T\mathbf{v}\\ \\ & ={\mathbf{w}}^{T}A\mathbf{v}\end{array}\end{array}$$

 

이다. 따라서 

 

$$\begin{array}{}\text{(13)}& (\lambda -\mu ){\mathbf{w}}^T\mathbf{v}=0\end{array}$$

 

되어야 하는데 $\lambda \ne \mu$이므로 ${\mathbf{w}}^T\mathbf{v}=0$이 되어야 한다. 이로써 서로 다른 고유값에 해당하는 고유벡터는 서로 직각임이증명되었다.

 

정리하면 다음과 같다.

 

"실수 대칭행렬의 고유값과 고유벡터는 모두 실수값이다.

또한 서로 다른 고유값에 해당하는 고유벡터는 서로 직각이다."