파이썬(Python)이나 매트랩(Matlab) 등 대부분의 컴퓨터 언어에는 가우시안 또는 균등분포(uniform distribution)로부터 샘플을 생성하는 함수를 가지고 있다. 샘플을 생성하고 싶은 확률밀도함수는 알고 있지만 샘플을 생성하기가 어려울 때는, 균등분포를 갖는 랜덤변수 \(X \sim U[0,1]\)로부터 해당 확률밀도함수를 갖는 랜덤변수 \(Y\) 사이의 함수 관계식 \(Y=g(X)\)을 구하고, 균등분포로부터 추출한 샘플 \(x^{(i)}\)를 함수 관계식 \(y^{(i)}=g(x^{(i)})\)로 변환해서 사용하면 된다. 그러나 이 방법은 랜덤변수가 다차원(multi-dimension)을 갖거나 복잡한 확률밀도함수를 갖는 경우에는 적용하기가 어렵다.
만약 샘플을 추출하여 기댓값(expectation)을 계산하는 경우라면 간단한 방법이 있다. 중요 샘플링(importance sampling) 방법을 이용하는 것이다. 중요 샘플링은 기댓값을 계산하고자 하는 확률분포함수는 알고 있지만 샘플을 생성하기가 어려울 때 해당 확률분포함수 대신에 샘플을 생성하기가 쉬운 다른 확률분포함수를 이용해 기댓값을 추정하는 방법이다.
확률밀도함수 \(p(\mathbf{x})\)에 기반한 함수 \(f(\mathbf{x})\)의 기댓값은 다음과 같이 계산된다.
\[ \mathbb{E}_{\mathbf{x} \sim p(\mathbf{x})} \left[ f(\mathbf{x}) \right] = \int_{\mathbf{x}} f(\mathbf{x}) \ p(\mathbf{x}) \ d\mathbf{x} \]
기댓값 기호 \( \mathbb{E} [ \cdot ]\)의 아래 첨자 \( \mathbf{x} \sim p(\mathbf{x})\)는 기댓값을 계산할 때 확률밀도함수로 \(p(\mathbf{x})\)를 사용한다는 의미다. 위 식에 확률밀도함수 \(q(\mathbf{x})\)를 도입하여 식을 전개해 보자.
\[ \begin{align} \mathbb{E}_{\mathbf{x} \sim p(\mathbf{x})} \left[ f(\mathbf{x}) \right] &= \int_{\mathbf{x}} \frac{q(\mathbf{x})}{q(\mathbf{x})} f(\mathbf{x}) \ p(\mathbf{x}) \ d\mathbf{x} \\ \\ &= \int_{\mathbf{x}} \left( \frac{p(\mathbf{x})}{q(\mathbf{x})} f(\mathbf{x}) \right) \ q(\mathbf{x}) \ d\mathbf{x} \\ \\ &= \mathbb{E}_{\mathbf{x} \sim q (\mathbf{x})} \left[ \frac{ p(\mathbf{x}) }{ q(\mathbf{x})} f(\mathbf{x}) \right] \end{align} \]
여기서 \(q(\mathbf{x})\)는 \(p(\mathbf{x})\)와는 다른 확률밀도함수이다.
위 식에 의하면 \(p(\mathbf{x})\)에 기반한 함수 \(f(\mathbf{x})\)의 기댓값을 \(q(\mathbf{x})\)에 기반해 계산할 수 있다는 것을 알 수 있다.
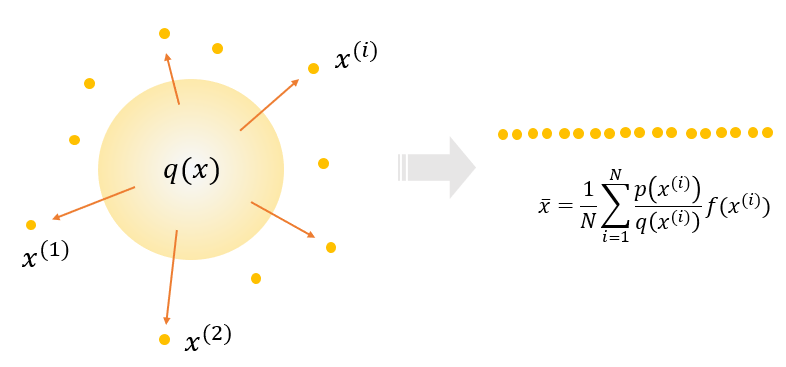
한편, 확률밀도함수 \(p(\mathbf{x})\)에 기반한 함수 \(f(\mathbf{x})\)의 분산(variance)은 정의에 의해서 다음과 같이 계산된다.
\[ var_{p(\mathbf{x})} \left[ f(\mathbf{x}) \right] = \mathbb{E}_{\mathbf{x} \sim p(\mathbf{x})} \left[ \left( f(\mathbf{x}) \right) ^2 \right] - \left( \mathbb{E}_{\mathbf{x} \sim p(\mathbf{x})} \left[ f(\mathbf{x}) \right] \right) ^2 \]
중요 샘플링의 분산도 정의에 의해서 다음과 같이 계산된다.
\[ var_{q(\mathbf{x})} \left[ \frac{p(\mathbf{x})}{q(\mathbf{x})} f(\mathbf{x}) \right] = \mathbb{E}_{\mathbf{x} \sim q(\mathbf{x})} \left[ \left( \frac{p(\mathbf{x})}{q(\mathbf{x})} f(\mathbf{x}) \right) ^2 \right] - \left( \mathbb{E}_{\mathbf{x} \sim q(\mathbf{x})} \left[ \frac{p(\mathbf{x})}{q(\mathbf{x})} f(\mathbf{x}) \right] \right) ^2 \]
두 분산의 크기를 비교하기 위해서 위 식을 좀 더 전개해보자.
\[ \begin{align} var_{q(\mathbf{x})} \left[ \frac{p(\mathbf{x})}{q(\mathbf{x})} f(\mathbf{x}) \right] &= \int_{\mathbf{x}} \left( \frac{p(\mathbf{x})}{q(\mathbf{x})} f(\mathbf{x}) \right) ^2 \ q(\mathbf{x}) \ d\mathbf{x} - \left( \mathbb{E}_{\mathbf{x} \sim p(\mathbf{x})} \left[ f(\mathbf{x}) \right] \right) ^2 \\ \\ &= \int_{\mathbf{x}} \frac{p(\mathbf{x})}{q(\mathbf{x})} \left( f(\mathbf{x}) \right) ^2 \ q(\mathbf{x}) \ d\mathbf{x} - \left( \mathbb{E}_{\mathbf{x} \sim p(\mathbf{x})} \left[ f(\mathbf{x}) \right] \right) ^2 \\ \\ &= \mathbb{E}_{\mathbf{x} \sim q (\mathbf{x})} \left[ \frac{ p(\mathbf{x}) }{ q(\mathbf{x})} \left( f(\mathbf{x}) \right) ^2 \right] - \left( \mathbb{E}_{\mathbf{x} \sim p(\mathbf{x})} \left[ f(\mathbf{x}) \right] \right) ^2 \end{align} \]
위 식을 확률밀도함수 \(p(\mathbf{x})\)에 기반한 함수 \(f(\mathbf{x})\)의 분산과 비교해 보면 중요 샘플링의 분산이 \(\frac{p(\mathbf{x})}{q(\mathbf{x})}\) 값에 따라서 원래 분산보다 매우 커질 수도 있음을 알 수 있다.
예를 들어보자.
함수를 \(f(x)=x\)로 놓고, 확률밀도함수 \(p(x)\)를 구간 \([0 1]\)의 균등분포로, \(q(x)\)를 평균이 0이고 분산이 1인 가우시안 분포라고 가정하자. 즉,
\[ \begin{align} p(x) &= \begin{cases} 1, & 0 \le x \le 1 \\ 0, & \mbox{else} \end{cases} \\ \\ q(x) &= \frac{1}{\sqrt{2 \pi}} \exp \left( - \frac{x^2}{2} \right) \end{align} \]
가우시안 분포 \(q(x)\)에서 \(500,000\)개의 샘플을 추출하여 이것으로 균등분포 \(p(x)\)를 사용했을 때의 기댓값을 계산해 보고자 한다. 기댓값의 정확한 값은 \(0.5\)이다. 참고로 정확한 분산은 \(0.0833\)이다.
먼저 가우시안 분포에서 추출한 샘플의 히스토그램을 그려본다.
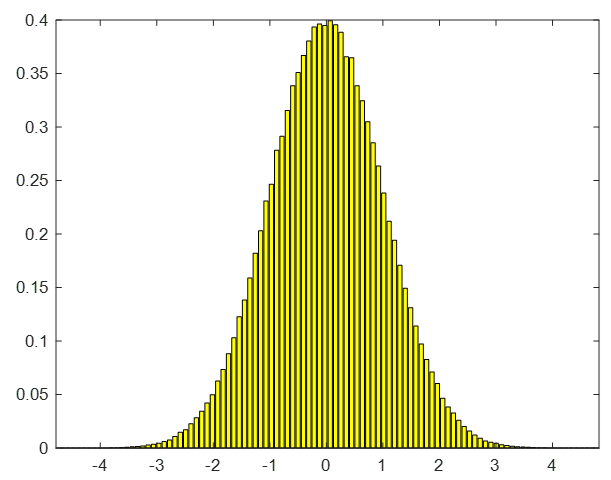
위 샘플을 이용하여 \( \frac{p(x)}{q(x)} x \) 의 샘플평균을 계산하면 \(0.5002\)로서 참값과 거의 같다. 하지만 샘플분산을 계산하면 \(0.8898\)로서 참값보다 매우 크게 나온다.
중요 샘플링은 강화학습과 파티클 필터(particle filter)에서 많이 사용되는 방법이다.
'AI 수학 > 랜덤프로세스' 카테고리의 다른 글
| [MCMC] MCMC 개요 (0) | 2024.12.26 |
|---|---|
| 정상 시퀀스 (Stationary Sequence) (0) | 2024.11.06 |
| 혼합 랜덤변수 (Mixed Random Variables) (0) | 2020.12.27 |
| 랜덤변수의 함수와 샘플링 - 3 (0) | 2020.12.26 |
| 랜덤변수의 함수와 샘플링 - 2 (0) | 2020.12.24 |




댓글