이산(discrete) 랜덤변수에서는 확률밀도함수(pdf, probability density function) 대신에 확률질량함수(pmf, probability mass function)를 사용한다. 이산 랜덤변수 \( \Theta \)의 확률질량함수 \( \omega_{\Theta} (\theta)\)는 다음과 같이 정의한다.
\[ \omega_{\Theta} (\theta_i ) = P \{ \Theta = \theta _i \} \]
여기서 \( \theta_i, \ i=1, ... , n \)은 표본 공간의 모든 원소다. 정의에 의하면 확률질량함수는 곧 확률임을 알 수 있다.
디랙 델타(Dirac delta)함수 \(\delta (\theta) \)를 이용하면 확률질량함수를 확률밀도함수의 형태로 표시할 수 있다.
\[ p_{\Theta} (\theta) = \sum_{i=1}^n \omega_{\Theta} (\theta_i ) \delta (\theta-\theta_i) \]
확률질량함수와 구별하기 위하여 확률밀도함수는 \( p_{\Theta} (\theta) \)로 표기한다.
연속 랜덤변수와 이산 랜덤변수가 함께 사용되면 혼합(mixed) 랜덤변수 문제라고 한다.
\(X\)를 연속(continuous) 랜덤변수라고 할 때 \(X=x\)로 주어진 \(\Theta \)의 조건부 확률질량함수 \( \omega_{\Theta | X} (\theta | x )\)는 다음과 같이 정의한다.
\[ \begin{align} \omega_{\Theta | X} (\theta | x ) &= \lim_{\Delta x \to 0 } \frac{ P \{ \Theta = \theta , x \lt X \le x + \Delta x \} }{ P \{ x \lt X \le x + \Delta x \} } \\ \\ &= \lim_{\Delta x \to 0 } \frac{ \omega_{\Theta} (\theta) \ p_{X | \Theta} (x | \theta ) \Delta x }{ p_X (x) \Delta x } \\ \\ &= \frac{ p_{X | \Theta} (x | \theta ) \ \omega_{\Theta} (\theta) }{ p_X (x) } \end{align} \]
위 식에 전확률(total probability) 정리를 대입하면, 혼합 랜덤변수 문제에서의 베이즈(Bayes) 정리를 다음과 같이 표현할 수 있다.
\[ \omega_{\Theta | X } ( \theta | x ) = \frac{ p_{X | \Theta } (x | \theta ) \ \omega_{\Theta} (\theta) }{ \sum_{\theta^\prime} p_{X | \Theta} (x | \theta ^\prime ) \ \omega_{\Theta} (\theta ^\prime ) } \]
혼합 랜덤변수 문제의 예를 들어보자.
다음과 같이 단순한 통신 채널이 있다.
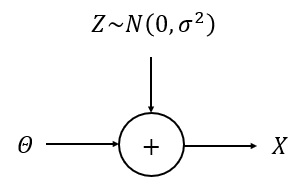
전달하고자 하는 신호는 이진(binary) 랜덤변수 \(\Theta \)로 표현할 수 있으며, 취할 수 있는 값과 확률은 다음과 같다.
\[ \Theta = \begin{cases} +1, & \mbox{with probability} \ \ p \\ -1, & \mbox{with probability} \ \ 1-p \end{cases} \]
수신한 신호 \(X\)는 노이즈 \(Z\)가 섞여 있는 \(X=\Theta +Z\)로 표현된다. 여기서 \(\Theta\)와 \(Z\)는 서로 독립이며, 노이즈 \(Z\)는 평균이 0이고 분산이 \(\sigma ^2\)인 가우시안 확률분포를 갖는다고 가정한다. 즉, \(Z \sim \mathcal{N} (0,\sigma ^2)\).
그렇다면 수신된 신호가 \(X=x\)로 측정되었을 때, \(\Theta \)의 조건부 확률밀도함수 \(\omega_{\Theta | X } (\theta | x ) \)를 어떻게 계산할 수 있을까.
먼저 문제에서 \(\omega_{\Theta } (+1) = p \), \(\omega_{\Theta} (-1) = 1-p \)가 주어졌고, \(p_{X | \Theta } (x | \theta ) = p_Z (x-\theta) \)이므로,
\[ \begin{align} X | \{ \Theta =+1 \} & \sim \mathcal{N} (+1,\sigma ^2) \\ \\ X | \{ \Theta =-1 \} & \sim \mathcal{N} (-1,\sigma ^2) \end{align} \]
이 된다. 따라서 베이즈 정리에 의하면,
\[ \begin{align} \omega_{\Theta | X} (+1 | x) &= \frac{ p_{X | \Theta} (x | +1) \omega_{\Theta} (+1) }{ p_{X | \Theta} (x | +1) \omega_{\Theta} (+1) + p_{X | \Theta} (x | -1) \omega_{\Theta} (-1) } \\ \\ &= \frac{ \mathcal{N} (+1,\sigma^2 ) \ p }{ \mathcal{N} (+1,\sigma^2 ) \ p + \mathcal{N} (-1,\sigma^2 ) \ (1-p) } \\ \\ &= \frac{ \frac{p}{\sqrt{2\pi\sigma^2}} \exp \left( - \frac{(x-1)^2}{2 \sigma ^2} \right) }{ \frac{p}{\sqrt{2\pi\sigma^2}} \exp \left( - \frac{(x-1)^2}{2 \sigma ^2} \right)+ \frac{1-p}{\sqrt{2\pi\sigma^2}} \exp \left( - \frac{(x+1)^2}{2 \sigma ^2} \right) } \\ \\ &= \frac{ p \exp \left( \frac{x}{\sigma ^2} \right) }{ p \exp \left( \frac{x}{\sigma ^2} \right) + (1-p) \exp \left( -\frac{x}{\sigma ^2} \right) } \end{align} \]
이 된다.
'AI 수학 > 랜덤프로세스' 카테고리의 다른 글
| 정상 시퀀스 (Stationary Sequence) (0) | 2024.11.06 |
|---|---|
| 중요 샘플링 (Importance Sampling) (0) | 2021.01.06 |
| 랜덤변수의 함수와 샘플링 - 3 (0) | 2020.12.26 |
| 랜덤변수의 함수와 샘플링 - 2 (0) | 2020.12.24 |
| 랜덤변수의 함수와 샘플링 - 1 (0) | 2020.12.22 |




댓글