랜덤 시퀀스의 정상성(stationarity)이란 랜덤 시퀀스의 확률적 특성 일부 또는 전부가 시불변(time-invariant)이라는 뜻이다. 정상 시퀀스에는 엄밀한 의미의 정상(SSS, strict-sense stationary) 시퀀스와 넓은 의미의 정상(WSS, wide-sense stationary) 시퀀스로 두 가지가 있다.
SSS 시퀀스는 임의의 싯점 \(t\) 와 임의의 차수 \(n\) 에 대해서 시퀀스 \( ( \mathbf{x}_t, \mathbf{x}_{t+1}, ... , \mathbf{x}_{t+n-1 }) \) 과 임의의 정수 \(h\) 만큼 시프트된 시퀀스 \((\mathbf{x}_{t+h}, \mathbf{x}_{t+1+h}, ... , \mathbf{x}_{t+n-1+h})\) 의 확률 분포가 서로 동일한 시퀀스를 말한다. 즉 시퀀스의 확률적 특성 전부가 시불변임을 의미한다.
\[ p(\mathbf{x}_t, \mathbf{x}_{t+1}, ... , \mathbf{x}_{t+n-1}) = p(\mathbf{x}_{t+h}, \mathbf{x}_{t+1+h}, ... , \mathbf{x}_{t+n-1+h}) \tag{1} \]
반면 WSS 시퀀스는 다음 두가지를 만족하는 시퀀스로 정의한다.
(1) 시퀀스 \(\{\mathbf{x}_t\}\) 의 평균함수(mean function)는 상수다. 즉,
\[ \mu_X [t]= const = \mu_X [0] \tag{2} \]
(2) 임의의 두 싯점 \(k, l\) 에서의 자기공분산함수(autocovariance function)와 임의의 정수 \(h\) 만큼 시프트된 싯점 \(k+h, l+h\) 에서의 자기공분산함수는 동일하다, 즉
\[ P_{XX} [k,l]=P_{XX} [k+h, l+h] \tag{3} \]
식 (3)과 같은 자기공분산함수를 시프트 불변성(shift-invariance)을 갖는다고 한다. 평균함수가 상수라면 자기공분산함수와 자기상관함수(autocorrelation function)의 시프트 불변성은 동일하다. 다음 두 식을 보자.
\[ \begin{align} & P_{XX} [k,l]= \mathbb{E} [(\mathbf{x}_k-\mu_X [k]) (\mathbf{x}_l-\mu_X [l])^T ] \tag{4} \\ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \mathbb{E}[\mathbf{x}_k \mathbf{x}_l^T ]-\mu_X [k] \mu_X [l] \\ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =R_{XX} [k,l]-(\mu_X [0])^2 \\ \\ & P_{XX} [k+h,l+h] = \mathbb{E}[(\mathbf{x}_{k+h}-\mu_X [k+h]) (\mathbf{x}_{l+h}-\mu_X [l+h])^T ] \tag{5} \\ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \mathbb{E}[\mathbf{x}_{k+h} \mathbf{x}_{l+h}^T ]-\mu_X [k+h] \mu_X [l+h] \\ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =R_{XX} [k+h,l+h]-(\mu_X [0])^2 \end{align} \]
식 (4)와 (5)로부터 다음 관계식을 얻을 수 있다.
\[ \begin{align} R_{XX} [k, l]=R_{XX} [k+h, l+h] \tag{6} \end{align} \]
따라서 (3)을 확인할 때 자기상관함수 (6)을 이용해도 된다.
WSS는 평균과 공분산(또는 상관관계) 함수만을 포함하는 약화된 종류의 정상성을 정의한다고 볼 수 있다. 왜냐하면 SSS 시퀀스는 WSS 시퀀스이지만 그 역은 성립하지 않기 때문이다. 증명하면 다음과 같다.
먼저 식 (1)에 의하면 임의의 싯점 \(t\) 에 대해 랜덤벡터 \(\mathbf{x}_t\) 의 확률밀도함수(pdf)는 \(\mathbf{x}_{t+(n-t)} = \mathbf{x}_n\) 의 확률밀도함수와 같다. 따라서 평균은
\[ \begin{align} \mathbb{E}[\mathbf{x}_n]= \mathbb{E}[\mathbf{x}_{t+(n-t)}]= \mathbb{E}[\mathbf{x}_t] \end{align} \]
이므로 모든 시간에서 동일한 평균값을 갖는다.
한편 두 랜덤벡터 \(\mathbf{x}_k\) 와 \(\mathbf{x}_l\) 의 결합(joint) 확률밀도함수는 \(\mathbf{x}_{k+h}\) 와 \( \mathbf{x}_{l+h}\) 의 결합 확률밀도함수와 같아야 한다. 따라서 자기상관함수는 다음과 같다.
\[ \begin{align} R_{XX} [k, l] &= \mathbb{E}[\mathbf{x}_k \mathbf{x}_l^T ] = \mathbb{E}[\mathbf{x}_{k+h} \mathbf{x}_{l+h}^T ] \\ \\ &=R_{XX} [k+h, l+h] \end{align} \]
자기공분산함수 또는 자기상관함수는 WSS 시퀀스에 대해 시프트 불변이므로, 하나의 매개변수만 갖는 함수로 정의하여 WSS 시퀀스의 표기를 단순화할 수 있다. 즉, 식 (3)과 (6)에서 두 싯점 \(k\) 와 \(l\) 의 시간 차가 \(n=l-k\) 라면,
\[ \begin{align} & P_{XX} [k, l] = P_{XX} [l-k]=P_{XX} [n] \tag{7} \\ \\ & R_{XX} [k, l]=R_{XX} [l-k]= R_{XX} [n] \end{align} \]
로 쓸 수 있다. 결국 WSS 시퀀스의 자기공분산함수와 자기상관함수는 두 싯점간의 시간 차 \(n=l-k\) 에만 의존한다.
증명은 다음과 같다. 두 랜덤벡터 \(\mathbf{x}_k\) 와 \(\mathbf{x}_l\) 의 결합 확률밀도함수는 \(\mathbf{x}_{k+(t-k)}= \mathbf{x}_t\) 와 \(\mathbf{x}_{l+(t-k)} = \mathbf{x}_{t+(l-k)}\) 의 결합 확률밀도와 같아야 한다. 따라서 자기상관함수는 다음과 같다.
\[ \begin{align} R_{XX} [k, l] &= \mathbb{E}[\mathbf{x}_k \mathbf{x}_l^T ] = \mathbb{E}[\mathbf{x}_t \mathbf{x}_{t+(l-k)}^T ] \\ \\ &=R_{XX} [t, t+(l-k)] \end{align} \]
위 식은 임의의 싯점 \(t\) 애서 항상 성립해야 하므로 자기상관함수는 두 싯점간의 시간차에만 의존한다. 따라서 \(R_{XX} [k, l]=R_{XX} [l-k]\) 로 표기할 수 있는 것이다.
스칼라 WSS 시퀀스인 경우 자기상관 함수 \(R_{XX} [n]\) 의 특징은 다음과 같다.
\[ \begin{align} & \mbox{(1) } \ R_{XX} [0]= \mathbb{E}[x_t^2 ] \ge 0 \tag{8} \\ \\ & \mbox{(2) } \ R_{XX} [n]=R_{XX}[-n] \tag{9} \\ \\ & \mbox{(3) } \ \lvert R_{XX} [n] \rvert \le R_{XX} [0] \tag{10} \end{align} \]
즉, 자기상관함수 \(R_{XX} [n]\) 는 \(n=0\) 일 때 최대값을 가지며 우함수(even function)라는 것을 알 수 있다.
식 (9)는 자기상관함수의 정의에 의해서 \(R_{XX} [n]= \mathbb{E}[x_t x_{t+n} ]= \mathbb{E}[x_{t+n} x_t ]=R_{XX} [-n]\) 이므로 쉽게 증명할 수 있다. 식 (10)은 슈워츠(Schwarz)의 부등식 정리에 의해서,
\[ \begin{align} (R_{XX} [n])^2 &= (\mathbb{E}[x_t x_{t+n} ])^2 \\ \\ & \le \mathbb{E}[x_t^2 ] \ \mathbb{E}[x_{t+n}^2 ] \\ \\ & = (R_{XX} [0])^2 \end{align} \]
이므로 역시 쉽게 증명할 수 있다.
자기상관함수와 자기공분산함수는 동일한 시퀀스 내에서 서로 다른 두 싯점에서의 랜덤벡터 사이의 상관도에 대한 정보를 준다. 자기상관함수의 값이 두 비교 싯점의 시간 간격이 커질수 록 급격히 작아진다면 두 싯점의 랜덤벡터 상관도가 급격히 떨어진다는 의미이고, 반대로 두 비교 싯점의 시간 간격이 커도 서서히 감소한다면 두 시점의 랜덤벡터의 상관도가 높다는 뜻이다. 서로 다른 두 싯점에서의 랜덤벡터가 비상관 관계에 있다면 이는 한 싯점에서의 확률 정보가 다른 싯점에서의 확률 정보를 추정하는 데 아무런 도움이 되지 않는다는 것을 의미한다. 다음 그림은 자기상관함수와 해당하는 랜덤 시퀀스의 샘플 예이다.

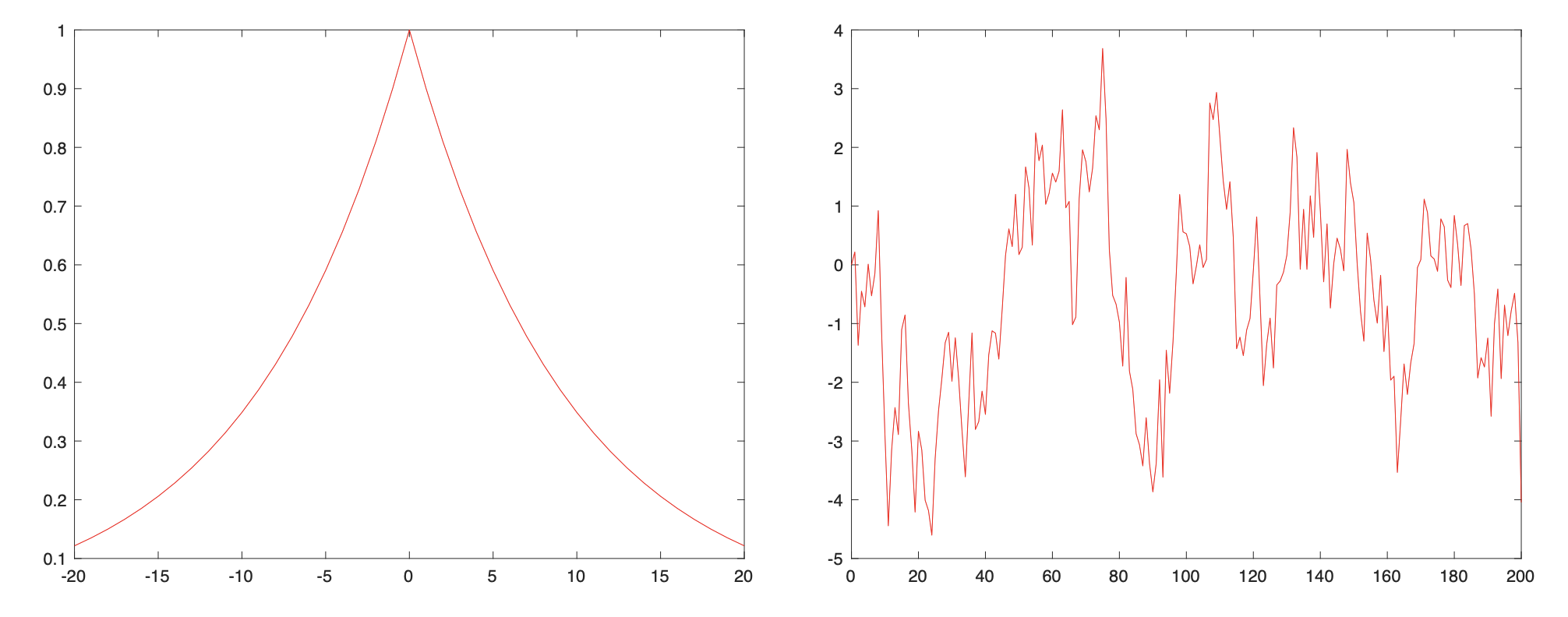
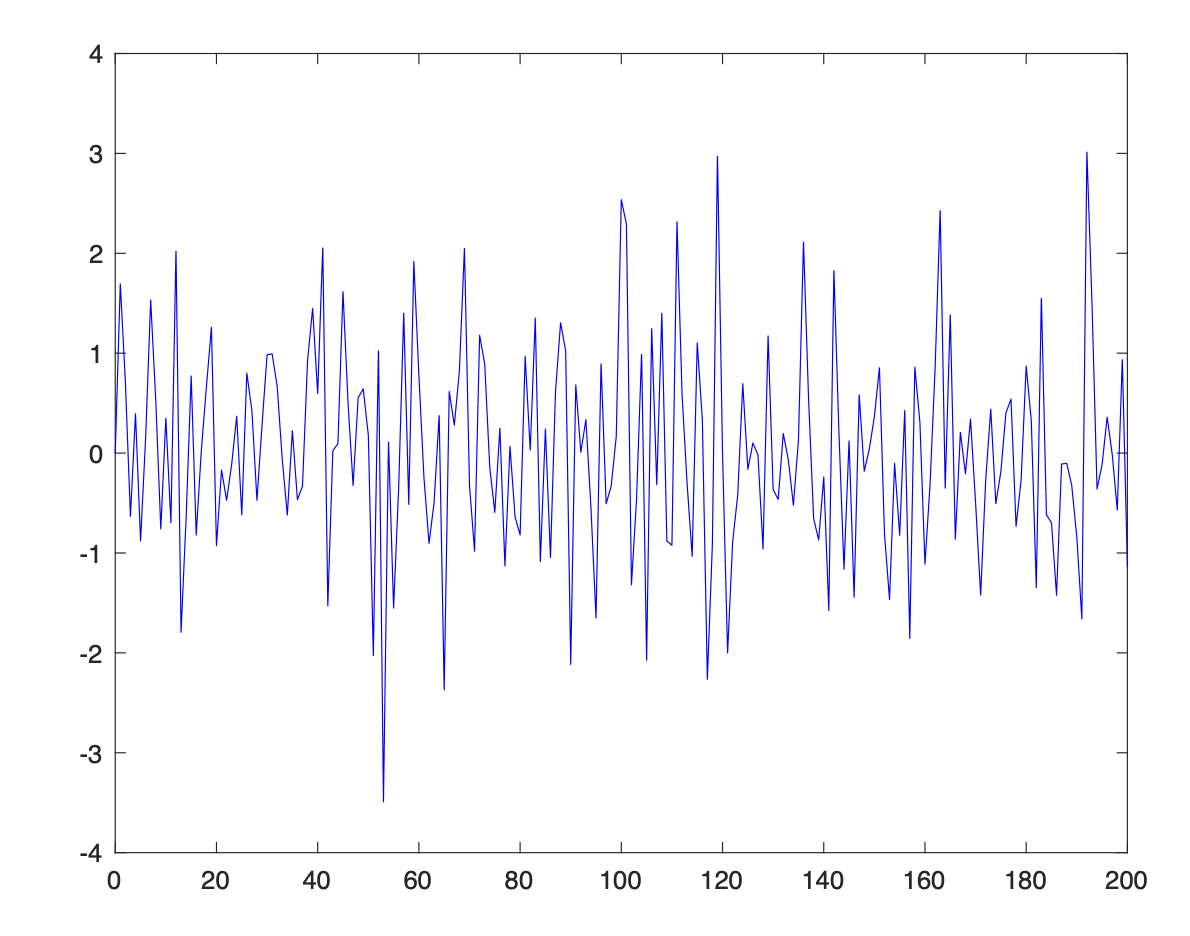
모든 싯점에서 비상관 관계에 있는, 즉 시간적으로 비상관 관계에 있는 랜덤 시퀀스를 이산시간 화이트 노이즈(white noise, 백색 잡음)라고 한다. 화이트 노이즈는 확정적(deterministic) 시스템에서 임펄스(impulse)의 개념과 유사한 신호로서, 자기상관함수가 다음과 같이 크로넥커 델타(Kronecker delta) 함수로 주어지는 넓은 의미의 정상(WSS) 시퀀스로 정의한다.
\[ \begin{align} \mathbb{E}[ \mathbf{w}_t \mathbf{w}_{t+n}^T ] =R_{WW} [n]=S_0 \delta_n \tag{11} \end{align} \]
여기서 \(\delta_n\) 는 크로넥커 델타 함수로서 다음과 같이 정의된다.
\[ \begin{align} \delta_n= \begin{cases} 1, & n=0 \\ 0, & n \ne 0 \end{cases} \end{align} \]
다음은 평균이 0인 화이트 노이즈의 예이다.
'AI 수학 > 랜덤프로세스' 카테고리의 다른 글
| [MCMC] 메트로폴리스-헤이스팅스 알고리즘 (0) | 2025.02.01 |
|---|---|
| [MCMC] MCMC 개요 (0) | 2024.12.26 |
| 중요 샘플링 (Importance Sampling) (0) | 2021.01.06 |
| 혼합 랜덤변수 (Mixed Random Variables) (0) | 2020.12.27 |
| 랜덤변수의 함수와 샘플링 - 3 (0) | 2020.12.26 |




댓글