언어 모델링이나 음성 인식, 강화학습 또는 주식 데이터 분석 등 시계열 데이터를 다루는 AI 분야에서는 매우 긴 시퀀스 데이터를 효과적으로 학습하고 표현(representation)할 필요가 있다. 그러나 모든 과거 데이터를 저장하고 처리하는 것은 저장 공간과 계산 자원의 한계로 인해 비효율적일 뿐만 아니라 실질적으로 불가능하다. 특히 온라인 환경에서는 데이터가 지속적으로 유입되기 때문에 이전 데이터를 적절히 요약(summarization)하면서도 중요한 패턴과 정보를 유지하는 메모리 메커니즘이 필요하다. 이러한 문제를 해결하기 위해 등장한 것이 바로 HiPPO (High-order Polynomial Projection Operators)다.
HiPPO는 '고차 다항식 투사 연산자'를 의미하는 것으로서 시간에 따라 변화하는 데이터를 다항식 기반의 최적화된 방법으로 압축 및 표현하여, 과거 데이터를 효율적으로 요약하면서도 새로운 데이터가 유입될 때마다 실시간으로 업데이트할 수 있는 수학적 도구다. 구체적인 내용은 다음 논문에 있으니 참고하기 바란다.
Albert Gu, Tri Dao, Stefano Ermon, Atri Rudra, and Christopher Re, "HiPPO: Recurrent Memory with Optimal Polynomial Projections", arXiv:2008.07669v2, Oct. 2020.
HiPPO 알고리즘은 직교 함수(orthogonal function)와 투사(projection)의 개념에 바탕을 두고 있으므로 이에 대한 사전 지식이 필요하다.
먼저 두 벡터 \(\mathbf{u}, \mathbf{v} \in \mathbb{R}^n\) 의 내적(inner product)은 다음과 같이 정의한다.
\[ \begin{align} \lt \mathbf{u}, \mathbf{v} \gt = \mathbf{u} \cdot \mathbf{v} = \sum_{i=1}^n u_i v_i \tag{1} \end{align} \]
만약 \( \lt \mathbf{u}, \mathbf{v} \gt =0\) 이면 두 벡터는 서로 직교(orthogonal)한다고 하고, \(\lt \mathbf{u}, \mathbf{v} \gt =1 \) 도 만족한다면 단위 직교(orthonormal)한다고 한다.
벡터의 경우와 마찬가지로, 구간 \([a, b]\) 에서 함수의 내적을 다음과 같이 정의할 수 있다.
\[ \begin{align} \lt f, g \gt_w = \int_a^b f(x) g(x) w(x) \ dx \tag{2} \end{align} \]
여기서 \(w(x) \gt 0\) 를 가중함수(weight function)라고 하며 \(f(x), \ g(x), \ w(x) \in \mathbb{R}\) 이다. 만약 두 함수가 \( \lt f, g \gt_w =0\) 이면, 구간 \([a, b]\) 에서 두 함수는 가중함수 기반에서 서로 직교(orthogonal)한다고 하고 \(\lt f, f \gt_w =1\), \(\lt g, g \gt_w =1\) 도 만족한다면 단위 직교(orthonormal)한다고 한다.
임의의 벡터 \(\mathbf{u} \in \mathbb{R}^n\) 는 단위 직교 벡터 \( \{ \mathbf{e}_0, \ \mathbf{e}_1, \ ..., \ \mathbf{e}_{n-1} \}\) 의 선형조합으로 표현할 수 있다.
\[ \begin{align} \mathbf{u} &= c_0 \mathbf{e}_0+c_1 \mathbf{e}_1+ \cdots +c_{n-1} \mathbf{e}_{n-1} \tag{3} \\ \\ &= \sum_{i=0}^{n-1} c_i \mathbf{e}_i \end{align} \]
여기서 \(\{ \mathbf{e}_0, \ \mathbf{e}_1, \ ..., \ \mathbf{e}_{n-1} \}\) 를 기저(basis) 벡터라고 하며 다음 성질을 갖는다.
\[ \begin{align} \lt \mathbf{e}_m, \mathbf{e}_n \gt =\delta_{mn}\tag{4} \end{align} \]
여기서 \(\delta_{mn}\) 는 크로넥커 델타 함수다. 단위 직교 벡터의 성질을 이용하면 식 (3)의 계수 \(c_k\) 는 다음 식으로 계산할 수 있다.
\[ \begin{align} \lt \mathbf{u}, \mathbf{e}_k \gt = \sum_{i=0}^{n-1} c_i \lt \mathbf{e}_i, \mathbf{e}_k \gt =c_k \tag{5} \end{align} \]
벡터의 경우와 마찬가지로, 함수 \(f(x)\) 도 구간 \([a, b]\) 에서 무한개의 단위 직교 함수 \(\{ \phi_0 (x), \ \phi_1 (x), \ \phi_2 (x), \ ... \}\) 의 선형조합으로 표현할 수 있다.
\[ \begin{align} f(x) &= c_0 \phi_0 (x)+c_1 \phi_1 (x)+c_2 \phi_2 (x)+ \cdots \tag{6} \\ \\ &= \sum_{i=0}^\infty c_i \phi_i (x) \end{align} \]
여기서 \(\{ \phi_0 (x), \ \phi_1 (x), \ \phi_2 (x), \ ... \}\) 를 구간 \([a, b]\) 에서의 기저(basis)함수라고 하며 다음 성질을 갖는다.
\[ \begin{align} \lt \phi_m, \phi_n \gt_w = \delta_{mn} \tag{7} \end{align} \]
단위 직교 함수의 성질을 이용하면 식 (6)의 계수 \(c_k\) 는 다음 식으로 계산할 수 있다.
\[ \begin{align} \lt f,\phi_k \gt_w = \sum_{i=0}^\infty c_i \lt \phi_i, \phi_k \gt_w =c_k \tag{8} \end{align} \]
원래 함수 \(f(x)\) 의 근사 함수 \(g(x)\) 는 무한 급수의 합 중에서 \(N-1\) 항까지만 더해서 얻을 수 있다.
\[ \begin{align} g(x)= \sum_{i=0}^{N-1} c_i \phi_i (x) \tag{9} \end{align} \]
이때 근사 함수 \(g(x)\) 는 원래 함수 \(f(x)\) 를 \(N\)차원 부분 함수공간 \(\{ \phi_0 (x), \ \phi_1 (x), \ ..., \ \phi_{N-1} (x) \}\) 에 투사(projection)하여 얻은 함수라고 한다.

이제 시간 구간 \([0, t ]\) 에서 함수 \(f(x) \in \mathbb{R}\) 를 근사화하는 방법에 대해서 생각해보자. 함수 \(f(x)\) 는 시계열 데이터를 발생시키는 함수이고 실시간으로 데이터를 계속 만든다고 가정한다. 즉 시간 구간 \([0, t]\) 에서 \(t\) 가 변수로서 계속 증가하는 상황을 생각하면 된다.
위에서 논한 바와 같이 함수 \(f(x)\) 를 단위 직교 함수로 이루어진 \(N\)차원 부분 함수공간 \(\{ \phi_0 (x), \ \phi_1 (x), \ ..., \ \phi_{N-1} (x) \}\) 에 투사하여 근사화하고자 한다. 그러면 식 (8)과 (9)에 의해서 근사 함수 \(g(x)\) 와 계수 \(c_k (t)\) 는 다음과 같이 계산할 수 있다.
\[ \begin{align} g(x) &= \sum_{i=0}^{N-1} c_i (t) \phi_i (x) \tag{10} \\ \\ c_k (t) &= \lt f, \phi_k \gt_w = \int_0^t f(x) \phi_k (x) w(x) \ dx \end{align} \]
식 (10)에서 계수 \(c_k\) 가 상수가 아니라 시간의 함수가 된 이유는 적분 구간 \([0, t ]\) 에서 \(t\) 가 변수이기 때문이다. 식 (10)은 가중함수 \(w(x)\) 와 기저함수 \( \{\phi_i (x) \}\) 를 정해야 계산할 수 있다. 논문에는 가중함수로서 3개, 기저함수로서 3개 정도의 함수가 언급되어 있는데 여기서는 그 중 균등(uniform) 가중함수와 르장드르 다항식(Legendre polynomials)을 기저함수로 사용한 조합에 대해서 설명한다. 논문에서는 이를 HiPPO-LegS 라 명명했고 성능이 제일 좋았다고 한다.
균등 가중함수는 구간 \([0, t]\) 에서 일정한 값을 갖는 함수로서 다음과 같이 주어진다.
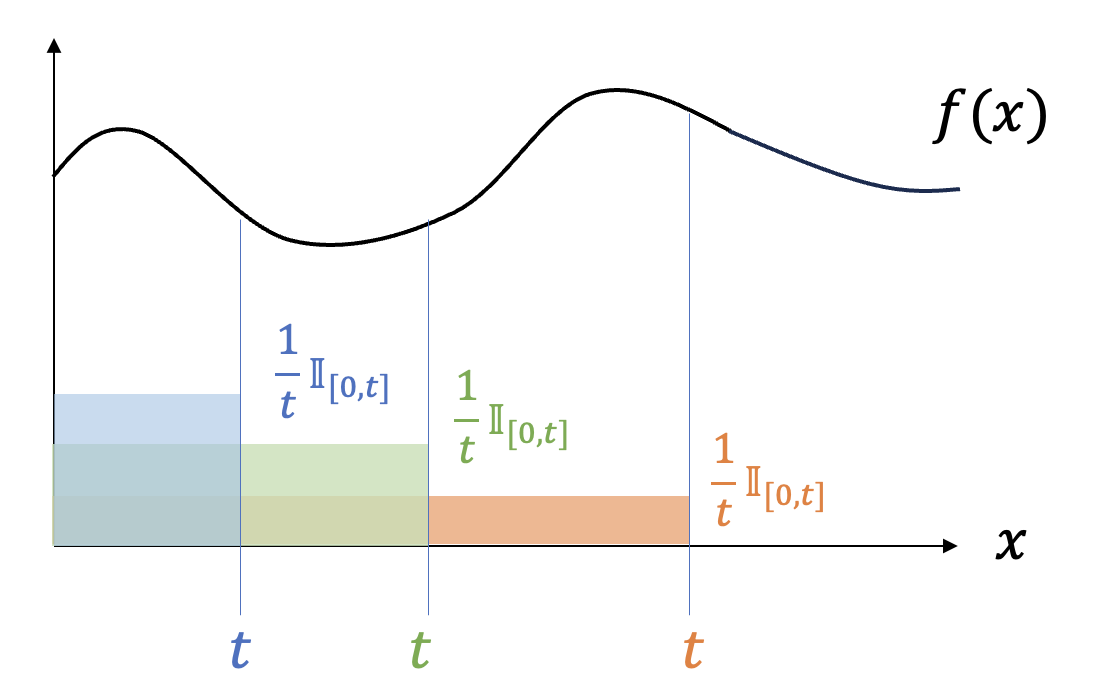
\[ \begin{align} w(t,x)= \frac{1}{t} \mathbb{I}_{[0,t]}, \ \ \ 0 \lt x \le t \tag{11} \end{align} \]
여기서 시간 \(t\) 가 변수이고 가중함수의 값이 \(t\) 에 따라 달라지기 때문에 \(w(x)\) 대신 \(w(t,x)\) 로 이를 명시하였다. \(\mathbb{I}_{[0,t]}\) 은 구간 \([0, t]\) 에서 \(1\) 의 값을 갖고 그 외의 구간에서는 \(0\) 의 값을 갖는 함수다.
식 (11)에 의하면 가중함수는 모든 시간 구간을 동일한 비중으로 고려하며 시간이 증가함에 따라 가중치를 다시 균등하게 재분배하는 것을 알 수 있다.
르장드르 다항식은 다음과 같이 직교 특성을 가지고 있다(https://pasus.tistory.com/175).
\[ \begin{align} \int_{-1}^1 P_m (\nu) P_n (\nu) \ d \nu= \frac{2}{2n+1} \delta_{mn} \tag{12} \end{align} \]
적분 구간이 \([-1, 1]\) 이므로 식 (10)의 적분 구간 \([0, t]\) 로 변환하기 위해서는 다음과 같이 적분 변수를 치환할 필요가 있다.
\[ \begin{align} \nu = \frac{2x}{t}-1 \tag{13} \end{align} \]
그러면 적분 구간은 \([-1, 1]\) 에서 \([0, t]\) 로 바뀌고, \(d\nu= \frac{2}{t} dx\) 이므로, 식 (12)는 다음과 같이 된다.
\[ \begin{align} & \frac{2n+1}{2} \int_0^t P_m \left( \frac{2x}{t}-1 \right) P_n \left( \frac{2x}{t}-1 \right) \frac{2}{t} \ dx \tag{14} \\ \\ & \ \ \ \ \ = (2n+1) \int_0^t P_m \left( \frac{2x}{t}-1 \right) P_n \left( \frac{2x}{t}-1 \right) \frac{1}{t} \ dx \\ \\ & \ \ \ \ \ = \delta_{mn} \end{align} \]
식 (11)의 균등 가중함수와 식 (14)를 고려하여 기저함수를 다음과 같이 선정한다.
\[ \begin{align} \phi_n (t,x) = \sqrt{(2n+1)} P_n \left( \frac{2x}{t}-1 \right) \tag{15} \end{align} \]
여기서 시간 \(t\) 가 변수이고 기저함수가 \(t\) 에 따라 달라지기 떄문에 \(\phi_n (x)\) 대신에 \(\phi_n (t,x)\) 로 표기했다. 일단 기저함수가 단위 직교 함수인지 확인해보자. 식 (14)를 이용하면,
\[ \begin{align} \lt \phi_m, \phi_n \gt_w &= (2n+1) \int_0^t P_m \left( \frac{2x}{t}-1 \right) P_n \left( \frac{2x}{t}-1 \right) \frac{1}{t} \mathbb{I}_{[0,t]} \ dx \tag{16} \\ \\ &=(2n+1) \int_0^t P_m \left( \frac{2x}{t}-1 \right) P_n \left( \frac{2x}{t}-1 \right) \frac{1}{t} \ dx \\ \\ &= \delta_{mn} \end{align} \]
이 되므로 기저함수는 구간 \([0, t]\) 에서 단위 직교 함수임을 알 수 있다. 식 (11)과 (15)를 식 (10)에 대입하면 근사 함수는 다음과 같이 된다.
\[ \begin{align} g(x) &= \sum_{n=0}^{N-1} c_n (t) \sqrt{(2n+1)} P_n \left( \frac{2x}{t}-1 \right) \tag{17} \\ \\ c_n (t) & = \int_0^t f(x) \sqrt{(2n+1)} P_n \left( \frac{2x}{t}-1 \right) \frac{1}{t} \ dx \end{align} \]
정리하면, 함수 \(f(x), \ 0 \lt x \le t\) 를 \(N\)차원 부분 함수공간으로 투사한 근사 함수 \(g(x), \ 0 \lt x \le t\) 는 식 (17)로 주어진다.
'AI 딥러닝 > Sequence' 카테고리의 다른 글
| HiPPO - 3 (0) | 2025.01.12 |
|---|---|
| HiPPO - 2 (0) | 2025.01.09 |
| [PtrNet] Pointer Net 구조 (0) | 2023.09.12 |
| [seq2seq] 어텐션이 포함된 seq2seq 모델 (0) | 2023.08.23 |
| [seq2seq] 간단한 seq2seq 모델 구현 (0) | 2023.08.17 |




댓글